분할정복을 이용한 거듭제곱 (JAVA)

📍 분할 정복을 이용한 거듭제곱

: 큰 수의 거듭제곱을 계산할 때 호율적으로 계산하기 위해서 사용되는 알고리즘이다.

1. 분할 정복(Divide and Conquer) 이란 ?

: 큰 문제를 더 이상 쪼갤 수 없이 작은 문제로 나눠 풀 다음 다시 그 문제들을 합쳐서 해결한다.

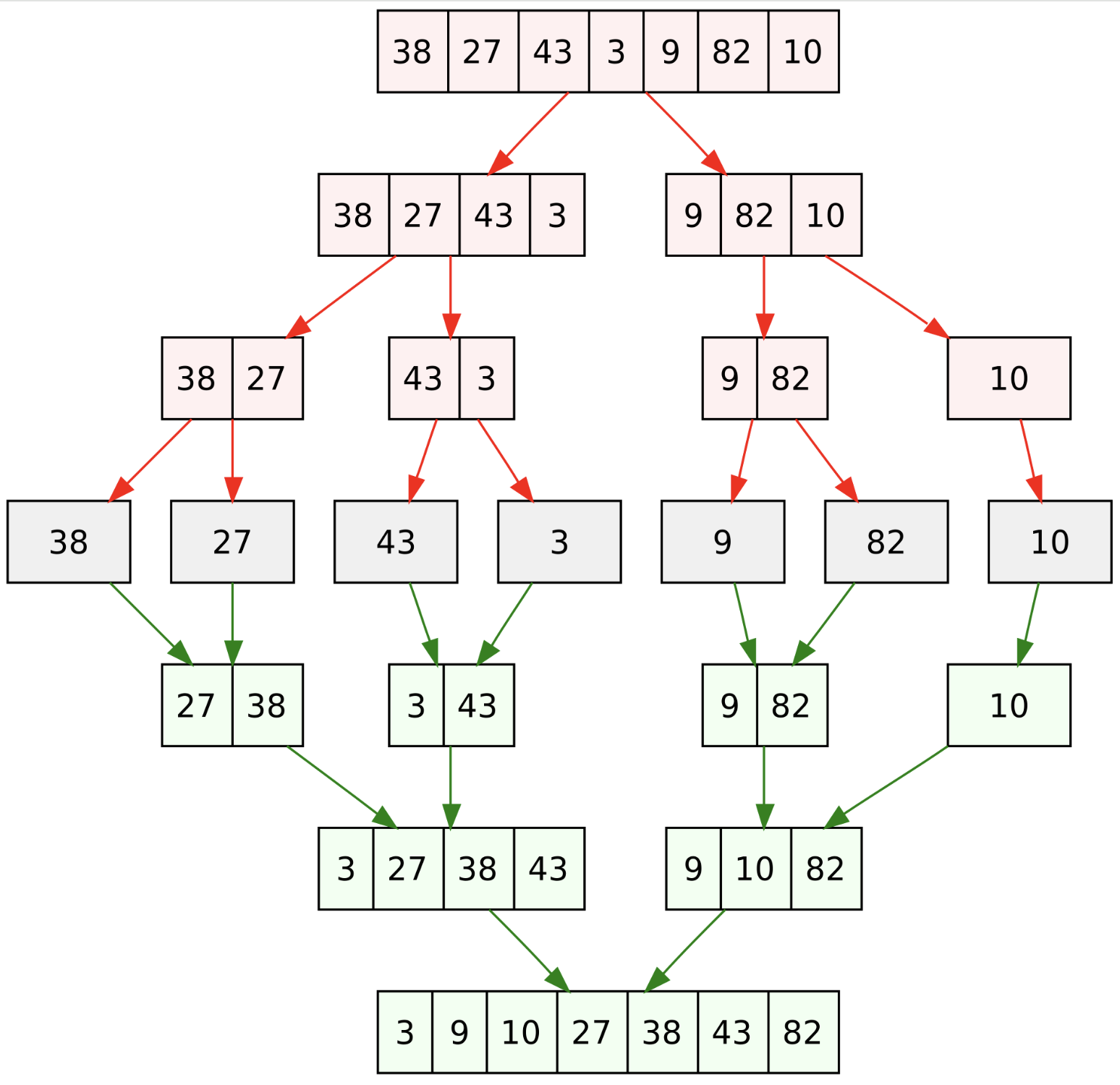- 사진 출처 : https://en.wikipedia.org/wiki/Divide-and-conquer_algorithm

2. 분할 정복을 이용한 거듭제곱

Cn = Cn/2 Cn/2 (n이 짝수일 때)
= C(n-1)/2 C(n-1)/2 * C (n이 홀수일 때)

위와 같이 거듭제곱 규칙을 활용한다.
이 방법을 사용하면 시간복잡도를 O(n)에서 O(log n)으로 줄일 수 있다.

3. 활용 (백준 문제)

https://www.acmicpc.net/problem/1629

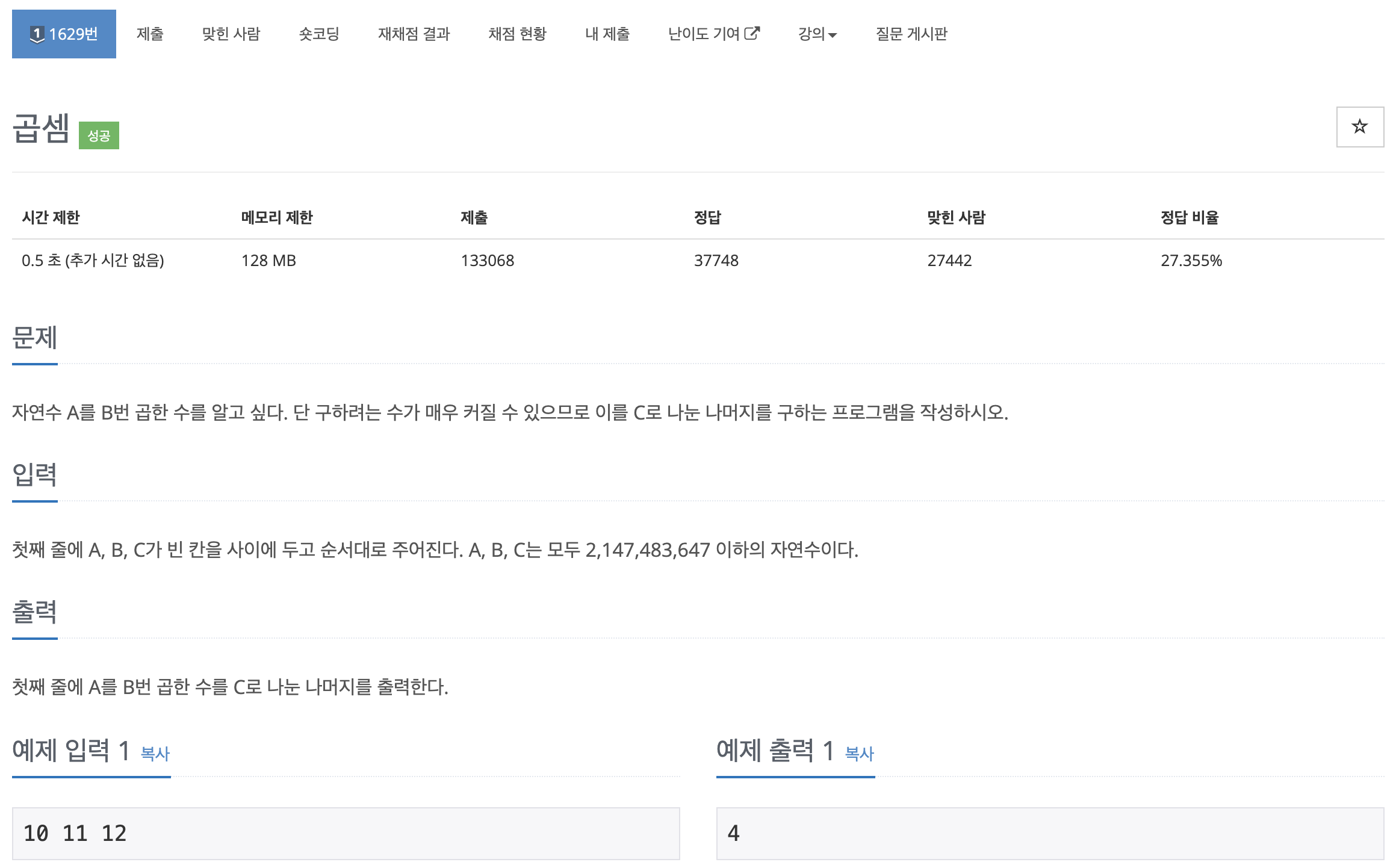
만약 위 거듭제곱 규칙을 생각하지 못 했다면 시간초과가 발생한다.

거듭제곱 규칙을 활용하여 이 문제를 푼다면

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());
        int A = Integer.parseInt(st.nextToken());
        int B = Integer.parseInt(st.nextToken());
        int C = Integer.parseInt(st.nextToken());

        System.out.println(mod(A, B, C));
    }

    public static long mod(int A, int B, int C) {
        long answer = A % C;
        if (B == 0) return 1;
        else if (B == 1) return answer;
        else {
            answer = mod(A, B / 2, C);
            answer = (answer * answer) %C;
            if (B%2 != 0 ) answer = answer *A %C;
            return answer;
        }
    }
}