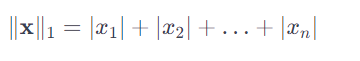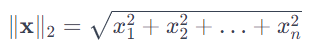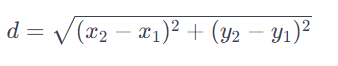미분

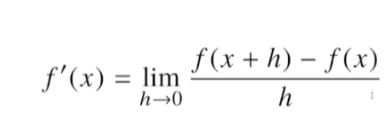
미분은 변수의 움직임에 따른 함수값의 변화를 측정하기 위한 도구
고등학교때 배웠던 극한의 개념.

import sympy as sym
from sympy.abc import x 

sym.diff(sym.poly(x**2 + 2*x +3),x ) #x로 미분하는 함수

Poly(2*x +2, x, domain='ZZ') # 결과값으로 왼쪽과 같이 나오게 된다.

요즘엔 컴퓨터로 미분이 가능한 시대라 손으로 할 필요는 없다.

• 미분은 함수의 주어진 점(x,f(x))에서의 접선의 기울기를 구한다.
• 이 미분값의 양,음수에 따라 증가하고있나 감소하고있나를 알 수 있다.
• 근데 바라보는 개념이 살짝 다르다. f`(x)의 값을 더하고 빼면서 함수값을 증,감을 시킨다.

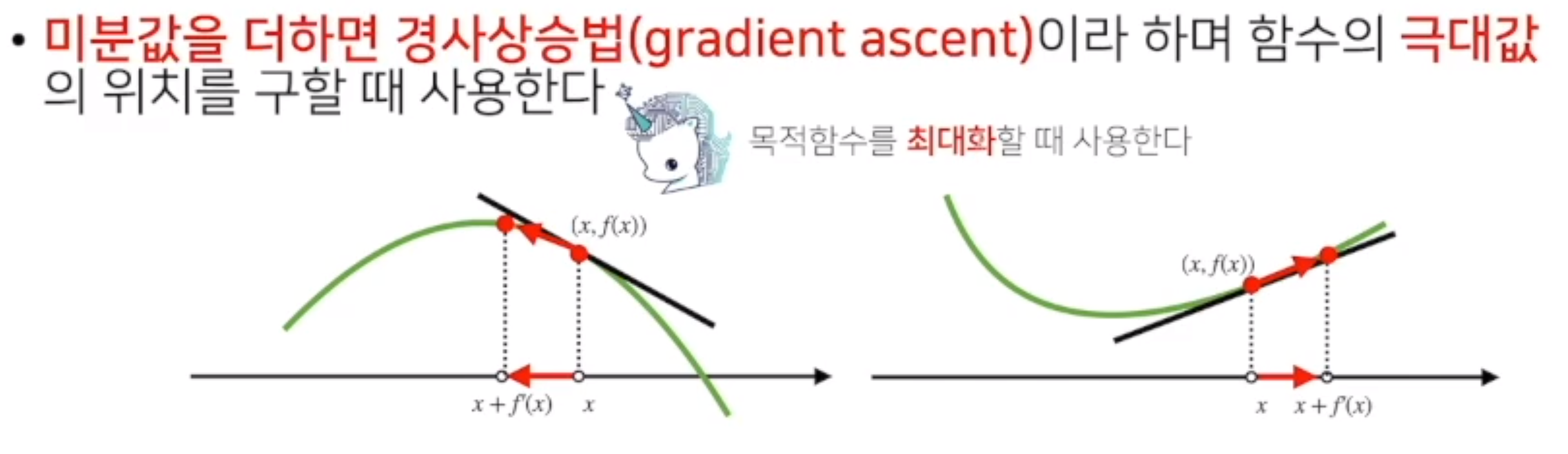
• 미분값을 더해주면 함수를 극대값의 위치를 구할때 쓰며 이를 경사상승법(gradient ascent)라고 한다.
• 경사상승,하강법은 극값에 도달하면 멈추게 된다.

경사하강법

Input : gradient, init, lr, eps, Output : var

gradient : 미분을 계산하는 함수

init: 시작점, lr: 학습률, eps: 알고리즘 종료 조건

var = init
grad = gradient(var)
while(abs(grad) > eps):
	var = var - lr * grad # 학습률을 잘 고려해서 정해야한다.
    grad = gradient(var)
    

만약 변수가 벡터이면?

입력이 다변수 함수의 경우 편미분(partial differentiation)을 사용해야한다.

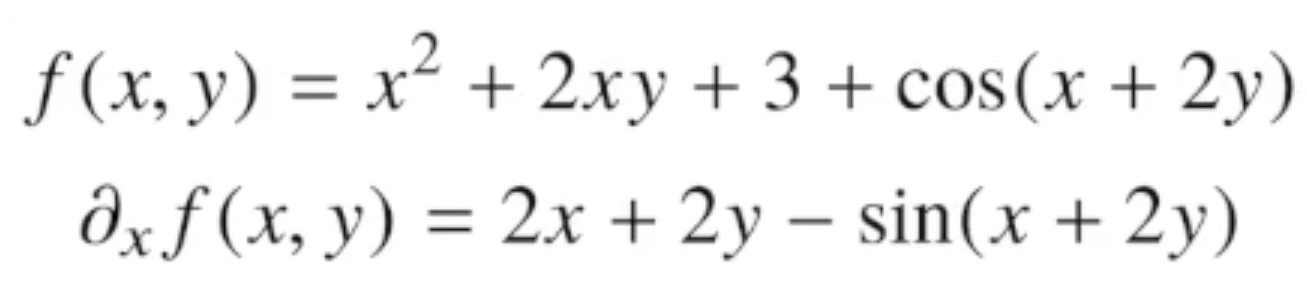
x를 편미분한다면, 나머지 변수 y는 그냥 상수 취급을한다.

• 각 변수 별로 편미분을 계산한 그레디언트(gradient) 벡터를 이용하여 경사하강/경사상승법에 사용할 수 있다.
  

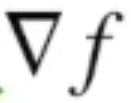
• nabla 라는 기호를 사용한다.

그레디언트 벡터

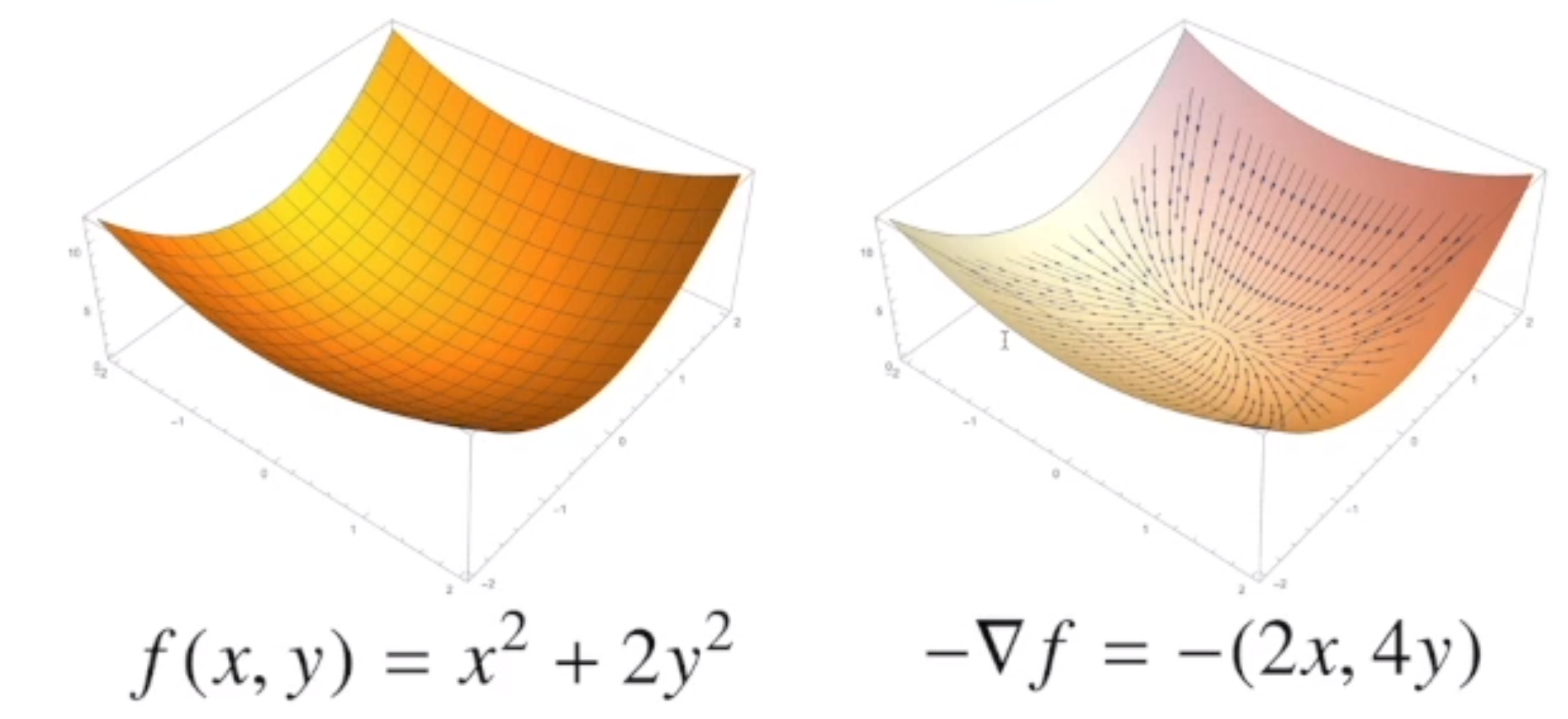
• 그레디언트 벡터를 보고 따라가면 해당 함수의 극점으로 이동 할 수 있다.
• 각 ∇f(x)는 점(x,y)에서 가장빨리 증가하는 방향이고,
• -∇f(x) = ∇f(-x)는 점(x,y)에서 가장 빨리 감소하는 방향이다.

경사하강법 알고리즘

• 경사하강법 알고리즘은 그대로 적용되지만, 벡터는 절대값 대신에 노름(norm)을 계산해서 종료조건을 결정한다.

var = init
grad = gradient(var)
while(norm(grad) > eps): # norm 을 사용 하는걸 주의.
	var = var - lr * grad 
    grad = gradient(var)

기습 복습! :

제1 노름 : 각 성분의 변화량을 절대값하여 더하기
L1-노름은 이상치에 덜 민감하고, 벡터의 희소성(sparcity)을 더 잘 반영하는 등의 장점이 있습니다.

제2 노름: 피타고라스 정리를 사용해 유클리드 거리를 계산
L2-노름은 가장 흔히 사용되는 노름 중 하나이며, 종종 벡터의 크기를 나타내는 데 사용됩니다.

유클리드란? :
우리가 학교다닐때 많이 썻던 이 공식을 말함.

실제 파이썬 구현

함수 : f(x) = X2 + 2x + 3 일때 경사하강법으로 최소점을 찾는 코드

def func(val):
	fun = sym.poly(x**2+2+x+3)
    return fun.subs(x, val), fun
    
def func_gradient(fun, val):
	_, function = fun(val)
    diff = sym.diff(function, x)
    return diff.subs(x, val), diff
    
def gradient_descent(fun,init_point,lr_rate=1e-2, epsilon = 1e-5):
	cnt = 0
    val = init_point
    diff,_=func_gradient(fun,init_point)
    while np.abs(diff)> epsilon:
    val = val - lr_rate*diff
    diff, _ = func_gradient(fun,val)
    cnt+=1
 	print('함수:{}, 연산횟수: {},최소점:({},{})".format(fun(val)[1],cnt,val,fun(val)[0]))

gradient_descent(fun*func,init_point*np.random.uniform(-2,2))

경사 하강법 기반 선형 회귀 알고리즘

X = np.array([[1,1], [1,2], [2,2], [2,3]])
y = np.dot(X, np.array([1,2])) + 3

beta_gd = [10.1, 15.1, -6.5]
X_ = np.array([np.append(x,[1]) for x in X]) #intercept 항 추가

for t in range(100): # 100이 학습횟수
	error = y - X_ @ beta_gd
    # error = error / np.linalg.norm(error)
    grad = -np.transpose(X_) @ error
    beta_gd = beta_gd - 0.01 * grad # 0.01이 러닝레이트. 
print(beta_gd)