행렬은 벡터를 원소로 가지는 2차원 배열이다.

x = np.array([[1,-2,3],
		  	 [7,5,0],
			 [-2,-1,2]])

3개의 행벡터를 하나의 array 벡터에서 표현.

열벡터가 아니라 행벡터를 원소로 가진다고 생각하자.

이후 행렬의 곱셈에서 더 이해하기 쉬워진다.
코딩테스트를 했으면 그대로 이해하면 될듯.

행벡터와 열벡터를 부르는 방법을 익혀두자.

만약에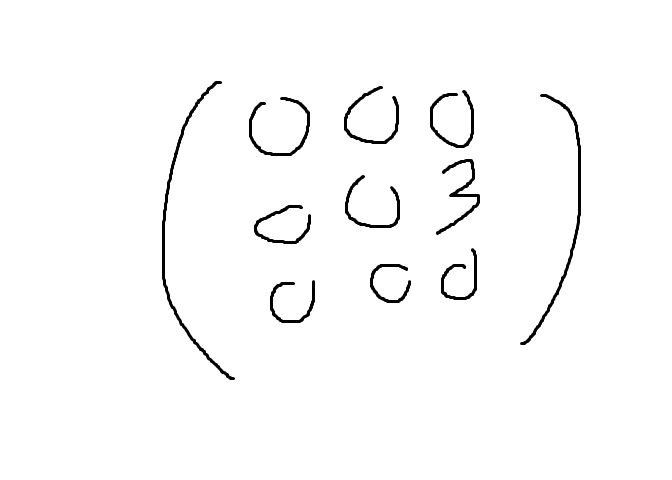

위에서 보이는 원소값3 을 부른다면 X32 로 나타낼 수 있다.

벡터끼리 모양이 같으면 사칙연산이 되기에, 행렬도 모양이 같으면 사칙연산이 가능하다.
각 성분곱들은 각 인덱스번호에 맞는 요소값끼리 곱하면 된다.
각 스칼라곱도 벡터와 차이가 없다.

단, 행렬 곱셈(matrix multiplication)은 다르다.

• 행렬곱셈 연산자는 @을 사용하고 곱할때 각 A의 행과 B의 열이 같아야한다.

  

• 그렇다면 행렬은 내적을 구할 수 있을까?

  

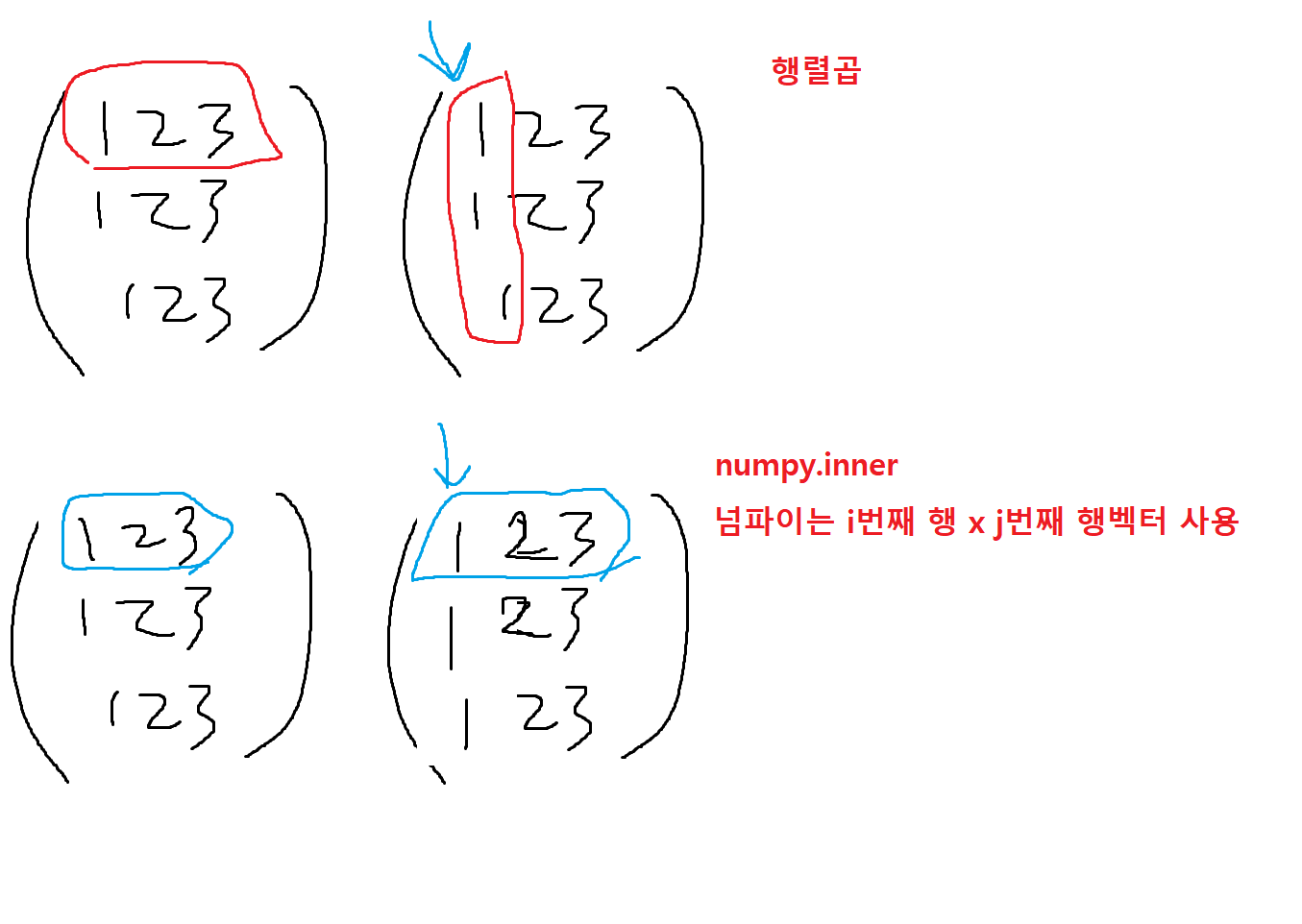
  np.inner 을 사용하면 i번째 행벡터와 j번째 행벡터 사이의 내적을 성분을 가지는 행렬을 계산한다.
  x라는행렬과 y라는행렬의 행렬곱을 사용한다.
  결과가 굉장히 다르다.

• 그렇기 때문에 두행렬의 내적은 두행렬의 행벡터의 크기가 같아야한다.

  행렬을 이해하는방법 (2)

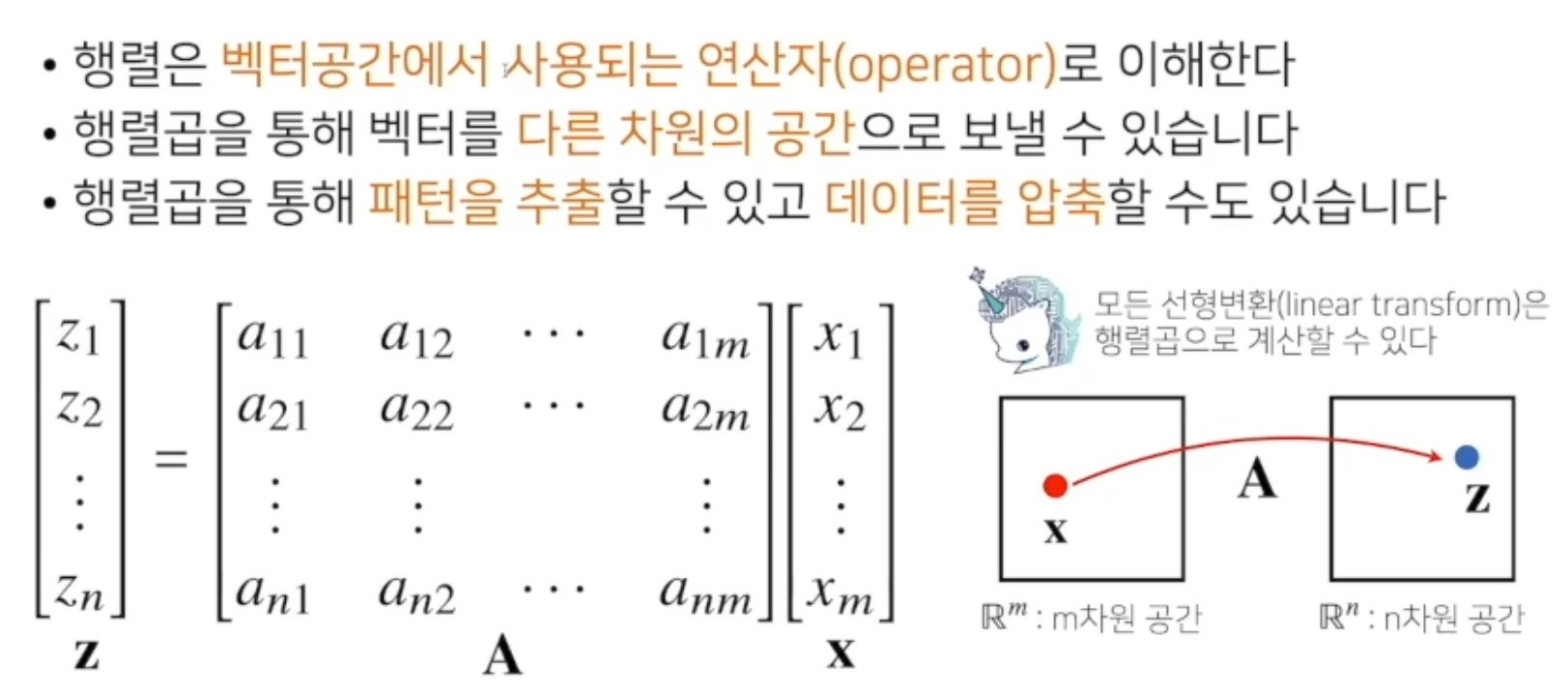
• 행렬곱을 통해 벡터를 다른차원의 공간으로 보낼 수 있다.

• 행렬은 벡터공간에서 사용되는 연산자로 이해한다.

• 행렬 곱을 통해 패턴을 추출 할 수 있고 데이터를 압축할 수도 있다.

  모든 선형변환은 행렬곱으로 나타낼 수 있다.

  

• 딥러닝은 선형변환과 비선현변환의 합성으로 이루어져 있다.

  numpy 에서 역행렬 구하는방법

  
  np.linalg(리니어알제브라).inv(x) 
  # 1. 행과 열의 숫자가 같아야함.
  # 2. 주어진 행렬의 디터미넌트가 0이면 안된다. (역행렬이 없으면안됨)
  
  # !! 아! 우리 고등학교 수학시간때 
  # !! 역행렬이 존재하나 체크하던 x11 * x22 - x21 * x12 를 말한다!

사실 역행렬을 계산 할 수없으면 , 유사 역행렬을 이용한다.

유사 역행렬 (pseudo-inverse) 또는 무어-펜로즈(Moore-Penrose) 역행렬 A+

이걸 사용하면 행과 열의 숫자가 달라도, 역행렬과 유사한 행렬을 사용 할 수 있다.

만약 주어진 행렬에서 행의 개수가 많은경우, 열의 개수가 많은 개수에 따라 유사 역행렬을 계산하는 방식이 달라진다.

n은 행, m은 열

m차원 공간과 n차원 공간으로 변환시킬때
n차원 공간벡터를 m차원으로 복원시킬때 사용하는 행렬 A +로이다.

#유사 역행렬
np.linalg.pinv(Y) # pinv 로 사용한다. 

단, 행과 열의 개수가 다를때 기능이 달라진다.

• 행이 더 클때 유사 역행렬은 원래 행렬보다 더 먼저 곱해줘야한다.

• 열이 더 클때 유사 역행렬을 원래 행렬보다 나중에 곱해줘야한다.

  np.linalg.pinv 를 이용하면 연립방정식의 해를 구할 수 있다.

a11X1+ ... a1mXm = b1
.
.

an1X1+ ... anmXm = bn

위를 정리하면
Ax = b로 정리할 수 있다.

이걸 유사 역행렬을 통해 구해보자.
x = A+b
x = AT(AAT)-1b

로 구할 수 있다. n <= m 이여야함. >

n,m에 따라 무어 팬던트 방정식이 달라지니까 유의!

즉, A의 왼쪽에다가 유사 역행렬을 곱해주면
왼쪽의 연립방정식을 만족하는 x의 해를 구할 수 있다.
x를 가지고 실제 식에 대입해보면 연립방정식을 만족하는 해가 된다.

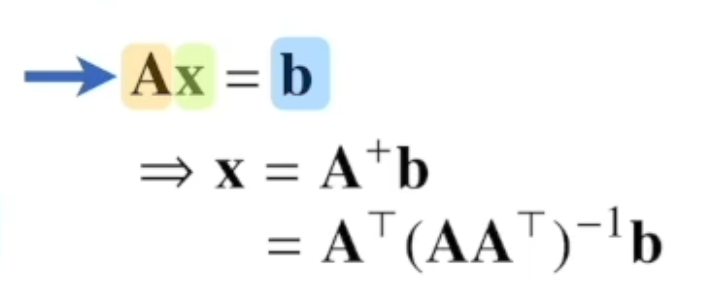
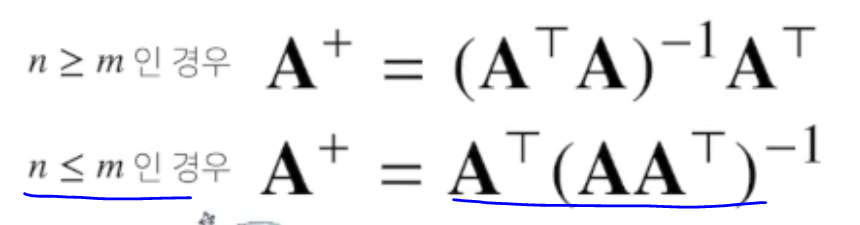
선형회귀분석

np.linalg.pinv를 이용하면 데이터를 선형모델(linear model)로 해석 하는 선형 회귀식을 찾을 수 있다.

• Y 절편 항을 고려해줘야한다.
  (n >=m 으로 데이터가 변수개수보다 많거나 같아야한다. )
  

이놈도 유사 역행렬을 사용 할 수 있다.

Xβ = y
선형 회귀분석은 x와 y가 주어진 상황에서 계수 β 를 찾아야한다.

• 선형회귀분석은 연립방정식과 달리 행이 더 크므로 방정식을 푸는건 불가능.

  

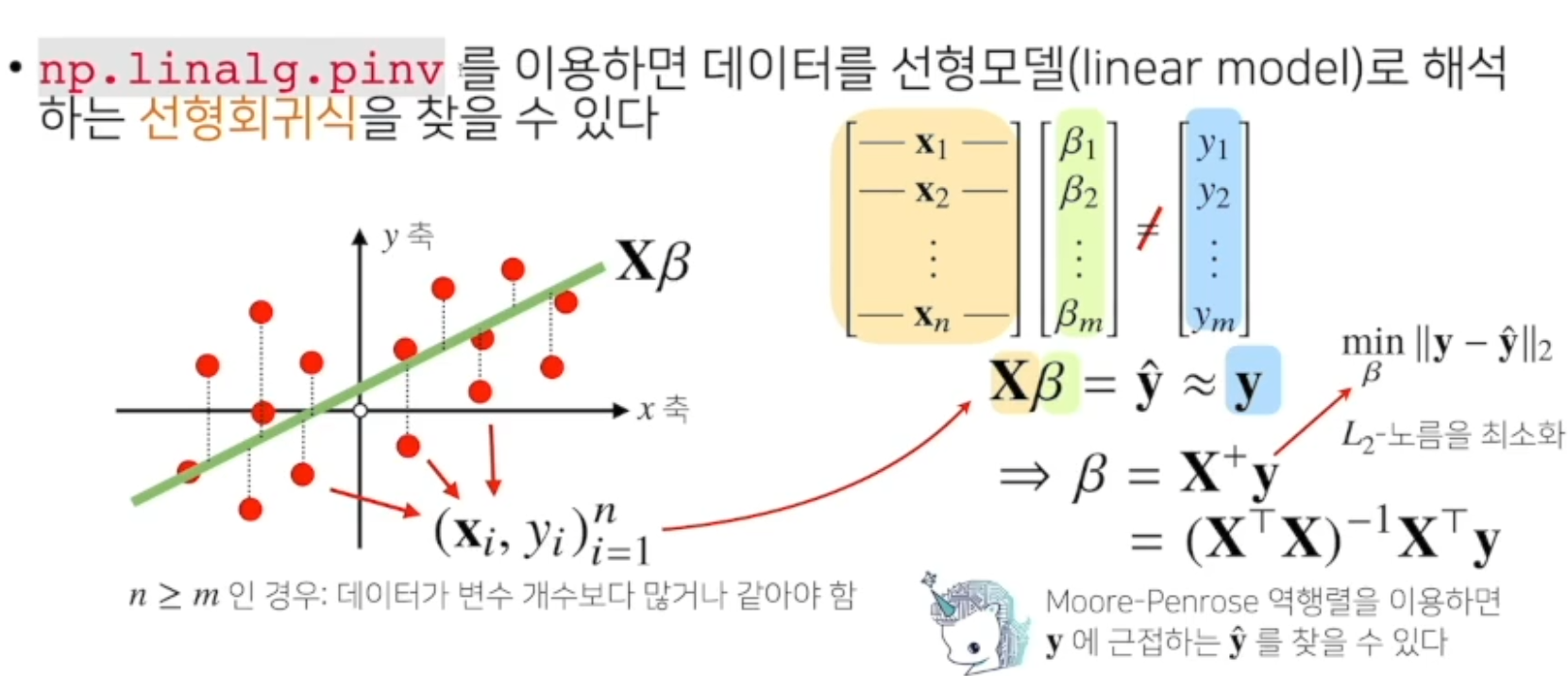
  구할 수 있는 최선의 모델은 유사한 y값을 무어-팬로즈 역행렬을 사용하여 찾는다.
  y에 가장 근접한 L2노름을 이용했을때 가장 근접한 y햇을 찻을 수 있다.
  이때 찾은 β 우리가 찾고자하는 선형회귀계수다.

• sklearn(싸이킷 런) 의 LinearRegression 과 같은 결과를 가져 올 수 있다.

  from sklearn.linear_model import LinearRegression
  model = LinearRegression()
  model.fit(X, y)
  Y_test = model.predict(x_test)
  
  # Moore-Penrose 역행렬
  beta = np.linalg.pinv(X) @ y
  y_test = np.append(x_test) @ beta

  -> 두개의 Y_test 값이 다르게 나올텐데 그 이유는
  y좌표를 고려해줘야한다. sklearn 은 자동으로 y를 보정해준다.

  무어 역행렬을 쓸때 y절편 1개를 직접 추가해줘야 원하고자하는 선형회귀분석이 가능하다. 이때 scikit learn과 같은 값이 나오게 된다.

  from sklearn.linear_model import LinearRegression
  model = LinearRegression()
  model.fit(X, y)
  Y_test = model.predict(x_test)
  
  # Moore-Penrose 역행렬
  X_ = np.array([np.append(x,[1]) for x in X])
  beta = np.linalg.pinv(X_) @ y
  y_test = np.append(x, [1]) @ beta

  후기

  열심히 받아적긴했지만 아직 이해가 잘가지않는다
  실제로 활용해보며 공부해봐야겠다!