시간 복잡도와 공간 복잡도
- 시간 복잡도 : 알고리즘의 수행시간을 의미하는 지표
- 공간 복잡도 : 알고리즘의 메모리 사용량
선택 정렬(selection sort)
- 데이터 중 가장 작은 값의 데이터를 선택하여 앞으로 보냄
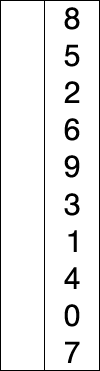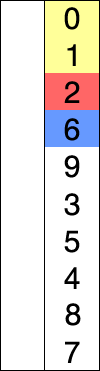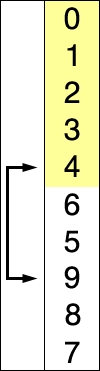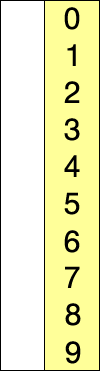
- worst, average, best 시간 복잡도 : O(n^2). 모두 동일
삽입 정렬(insertion sort)
- 데이터를 순서대로 뽑아 적절한 위치를 찾아 삽입함으로써 완성하는 정렬
- 자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교해 자신의 위치를 찾아 삽입
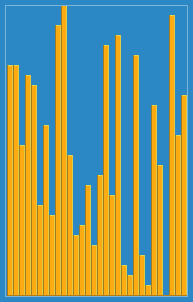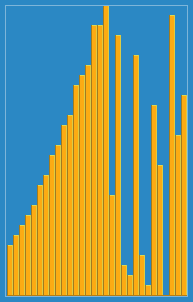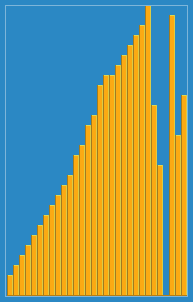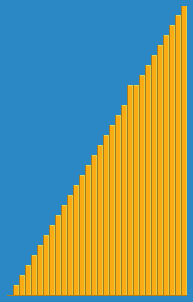
- 배열이 길어질수로 효율이 떨어짐
- 구현이 간단
- 무조건 위치를 변경하는 선택 정렬과 달리 필요할 때에 삽입한다는 점에서 효율적
- 이미 정렬된 데이터가 많으면 효율적
- best 시간 복잡도 : O(n)
- average, worst 시간 복잡도 : O(n^2)
버블 정렬(bubble sort)
- 옆에 있는 데이터와 비교하여 더 작은 값을 앞으로 보냄
- worst, average, best 시간 복잡도 : O(n^2)
- 선택 정렬, 삽입 정렬과 시간 복잡도가 같지만 연산 수가 많아 느리고 효율성 떨어짐
- 느리지만 코드가 단순해 사용
합병 정렬(merge sort)
- 비교 기반 정렬 알고리즘
- 분할, 정렬, 결합 순으로 진행되는데 데이터 배열을 2개 이상의 부분 배열로 분할고 부분 배열에서 정렬한 뒤 결합해 다시 정렬을 진행
- 데이터 배열 전체가 다시 결합되고 정렬되면서 마침
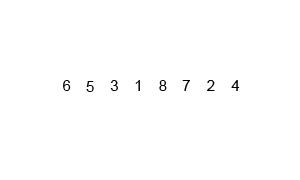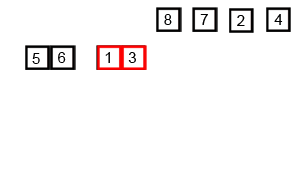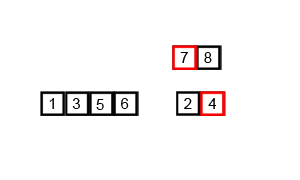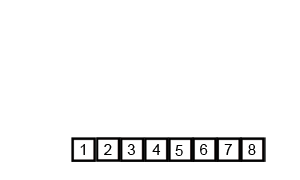
- worst, average, best 시간 복잡도 : O(NlogN)
- 장점
- 데이터를 정확히 반으로 나누고 정렬하기 때문에 항상 일정한 시간 복잡도 유지 -> 데이터 분포에 영향을 덜 받음. 퀵 정렬의 한계점 보완.
- 단점 : 다른 알고리즘과 비교했을 때 O(n) 수준의 메모리가 추가로 필요. 레코드를 배열(Array)로 구성하면, 임시 배열이 필요하기 때문
퀵 정렬(quick sort)
- 데이터 중 임의의 기준값을 정해 두 부분집합으로 나눔
- 이때 기준 값 : 피벗(pivot)
- 왼쪽은 피벗보다 작은 값, 오른쪽은 피벗보다 큰 값을 배치하고 더 이상 집합을 나눌 수 없을 때 까지 재귀적으로 실행
- average, best 시간 복잡도 : O(NlogN)
- worst 시간 복잡도 : O(n^2)
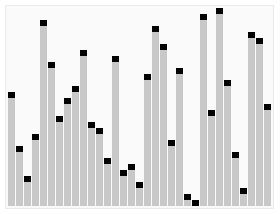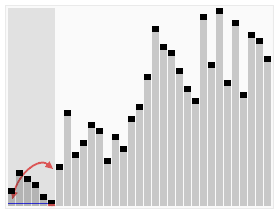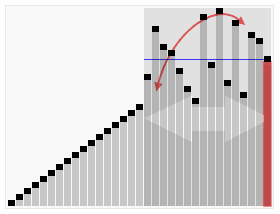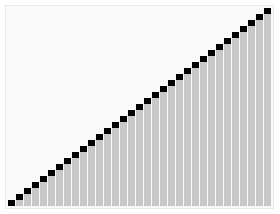
- 수평선은 피벗 값
- 정렬을 위해 평균적으로 O(logN) 만큼의 메모리를 필요로 함. 이는 재귀적 호출로 발생하는 것이며, 최악의 경우 O(n) 공간복잡도 가짐
- 이미 정렬된 데이터라면 매우 비효율적으로 동작