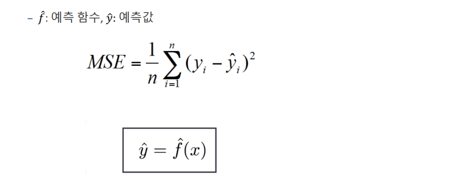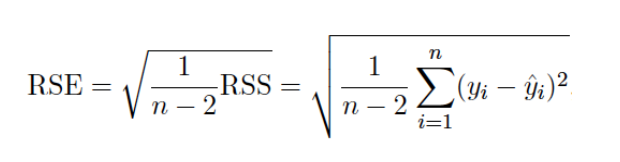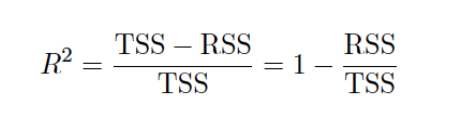DATA SCIENCE (1)

1. 통계 학습

: 데이터를 이해하기 위한 도구

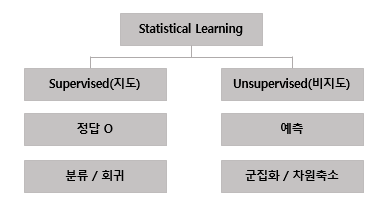
지도 통계 학습(Supervised statistical learning)

• 데이터 (x,y)가 주어졌을 때, 통계 모델을 통해 f(x)를 찾아내는 활동
• 모델 f를 이용하여 새로운 값 x에 대해서 y값 예측

비지도 통계 학습(Unsupervised statistical learning)

• 입력 데이터 x만 주어지고, 숨겨진 구조 학습
• x,y 입력 data만 존재 => 입축력 관계 X

2. Supervised (지도 학습)

1. 용어

01. Prediction(예측)

• f(x)를 black box 취급하여 예측값인 y에 초점
• 
• Direct Marketing
  : 각 사람당 400 종류의 데이터를, 9만명에 대해 가지고 있을 경우, 누가 얼마나 기부금을 낼 것인지 알고 싶은 경우

02. Inferece(추론)

• x의 각 요소들이 얼마나 y에 영향을 미치는지에 초점
• 광고, 부동산
  : 어떤 media가 매출에 영향을 미치는지
  : TV광고는 매출에 어느 정도 영향을 미치는지

03. Parametric Methods

• 함수 형태는 정해져 있고 파라미터만 결정

  STEP1 : 함수 형태 선택
  STEP2 : 학습 데이터(training data)를 이용하여 파리미터 결정

• 선형 모델의 경우, p+1개의 계수만 결정

04. MSE(Mean Squared Error)'

05. fitting

• Overfit(과적합):과도하게 유연한 모델의 경우 오히려 예측 정확도가 떨짐
  

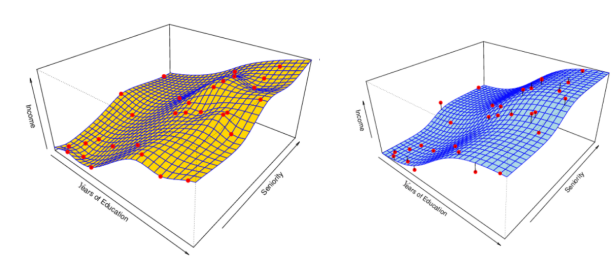
• Greatefit(최적합)

• Underfit(과소적합)

06. Train data vs Test data

• Train data : 모델 학습에 사용되는 데이터, 입력과 출력 간의 패턴과 관계를 학습, 일반화 하는데 사용
• Test data : 학습된 모델의 성능을 평가하기 위해 사용되는 데이터, 실제 성능 확인 역할
• Train MSE ≠ Test MSE
• Test data에 대한 MSE를 줄이는 것이 중요

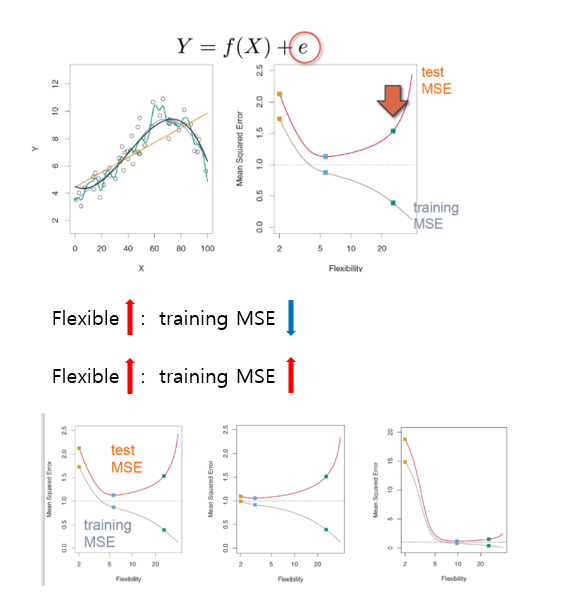
07. MSE 관계

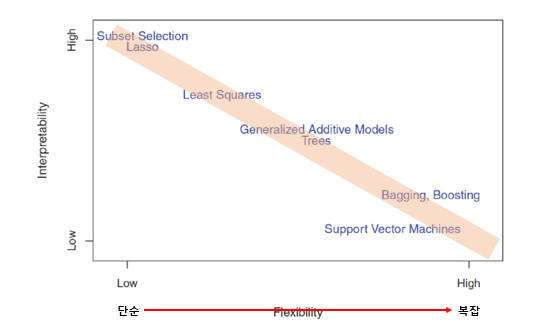
• Flexibility vs Interpretability (Trade off 관계)
  

• Irreducible ERROR까지 패턴을 찾기 위해 노력
  -> MSE는 증가 (overfitting)
  

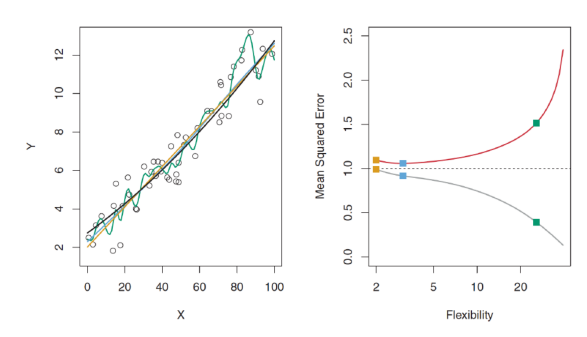
• 실제 f가 선형 함수인 경우
  

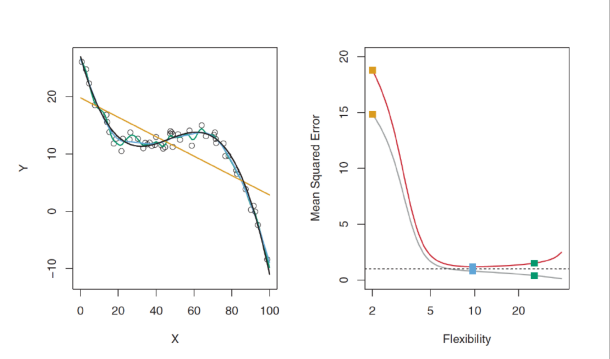
• 실제 f가 고차원 비선형 함수인 경우
  

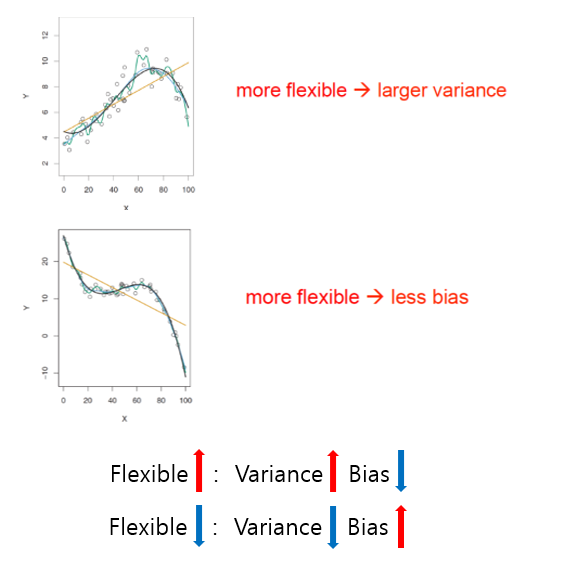
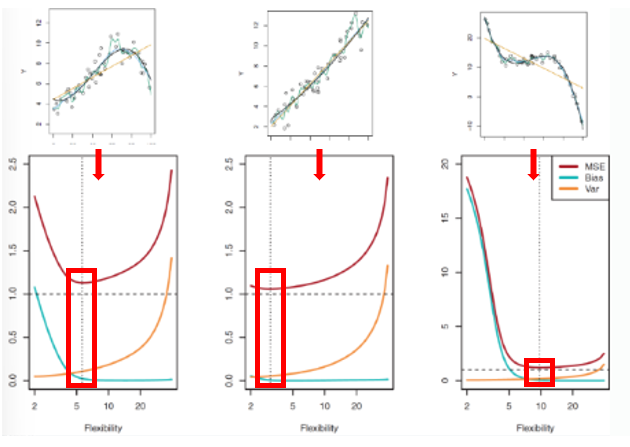
08. Bias-Variance Trade-off

• Bias : 모델의 예측값과 실제 값 간의 차이
• Variance : 모델의 예측값이 훈련 데이터에 대한 변동성
  

<결론>

• Vairance와 Bias 동시에 줄이기 불가
• Vairance와 Bias의 합이 최소가 되는점 -> GOOD
  

2. 분류 문제(Classification Problems)

: response Y -> quantitative가 아닌 qualitative/categorical

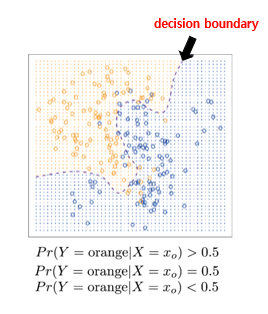
01. Bayes Classifier
: 데이터의 특징을 기반으로 각각의 클래스(카테고리)에 속할 확률을 계산하고, 가장 높은 확률을 갖는 클래스로 분류

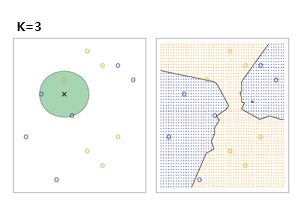
02. KNN(K-nearest neighbors classifier)
: 주어진 데이터 포인트의 주변에 위치한 K개의 최근접 이웃들을 기반으로 분류

03. Bayes vs KNN

• Bayes, KNN 비교 그래프
  

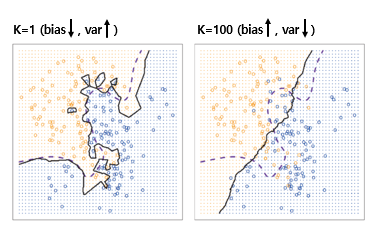
• K=1, K=100에서의 bias, var
  

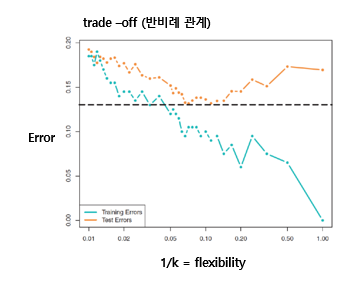
• bias, variance의 error, flexibility
  

3. 선형 회귀(Linear Regression)

01. Background

• 자료
  

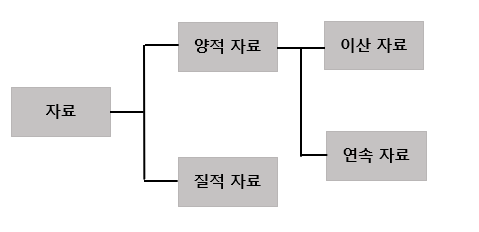
• 정규분포
  

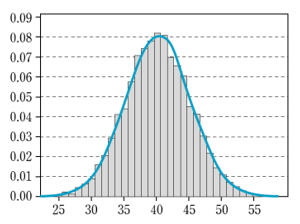
• 판정

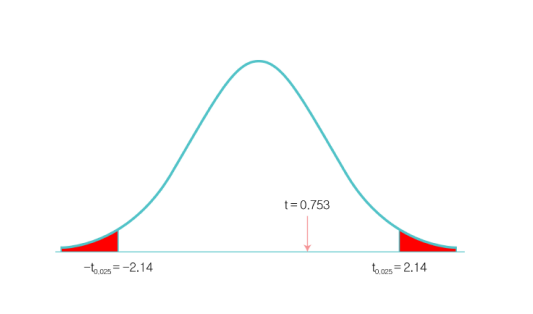
02. 선형 회귀 (Linear regression)
: 입력 변수와 출력 변수 간의 선형 관계를 모델링하는 예측 알고리즘
: 주어진 입력 데이터와 해당하는 출력 값으로 최적의 선형 함수 찾기
-> 새로운 입력에 대한 출력 값 예측
(* 실제 regression 함수들은 선형 X)

03. 파라미터 추정 : Least square

• 주어진 데이터를 기반으로 최적의 모델 파라미터 값을 찾는 과정
• 최소 제곱법(Least Square Method) 사용 -> 잔차 최소화

  i번째 잔차 = 실제 출력 값(i) - 예측 값(i)

• RSS(Residual sum of squares)
  : 모델의 적합도 평가

  RSS = Σ(실제 출력 값(i) - 예측 값(i))^2
  

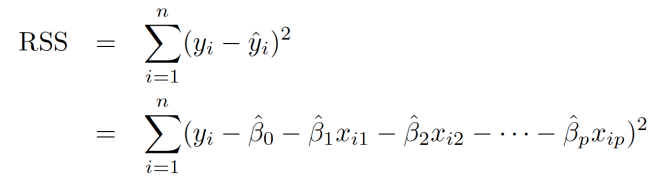
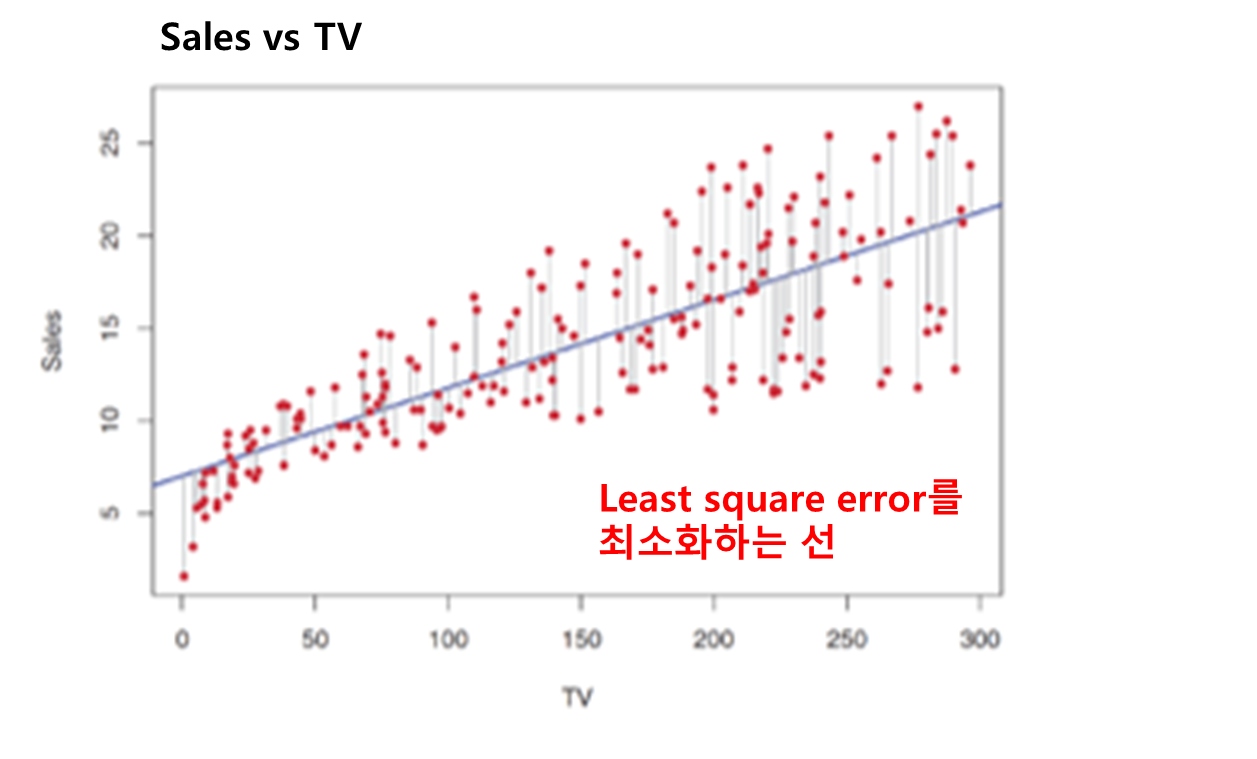
ex) Least square fit 예제

04. 모델 정확도 평가

표준에러 (Standard Error)

: estimate이 sample데이터에 대해 얼마나 바뀌는지 나태냄.

• 표본 평균 내에 존재하는 편차
• 참고 : 분산, 표준편자, 표준 에러
• X(i)가 넓게 퍼질수록 작은 SE값을 가짐

  

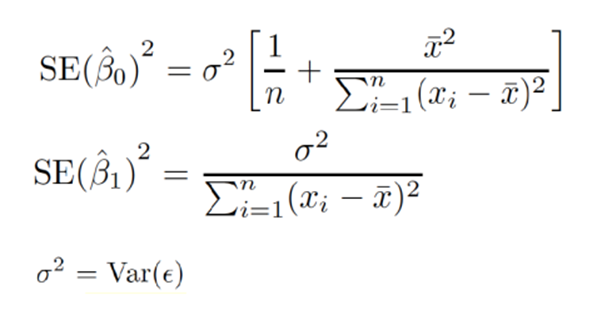
신뢰구간 (Confidence Interval)

• 표준 오차를 사용하여 신뢰구간 계산 가능
• 95% 신뢰 구간 : 95%의 확률로 해당 구간이 실제 파라미터값을 포함할수 있는 구간
  

05. 가설 테스트

t-static

: Null가설을 제외 -> X와 Y사이에 linear 연관성이 있음

Linear Regression 모델 정확도 평가

• RSE(Residual Standard Error)
  
• R^2 statistic
  
• 예제1 (Sales VS TV)
  : RSE -> 실제 모델을 찾아더라도 3.26 만큼 실제값과 떨어짐
  : 61%의 sales 변화율이 TV로 설명 가능
  

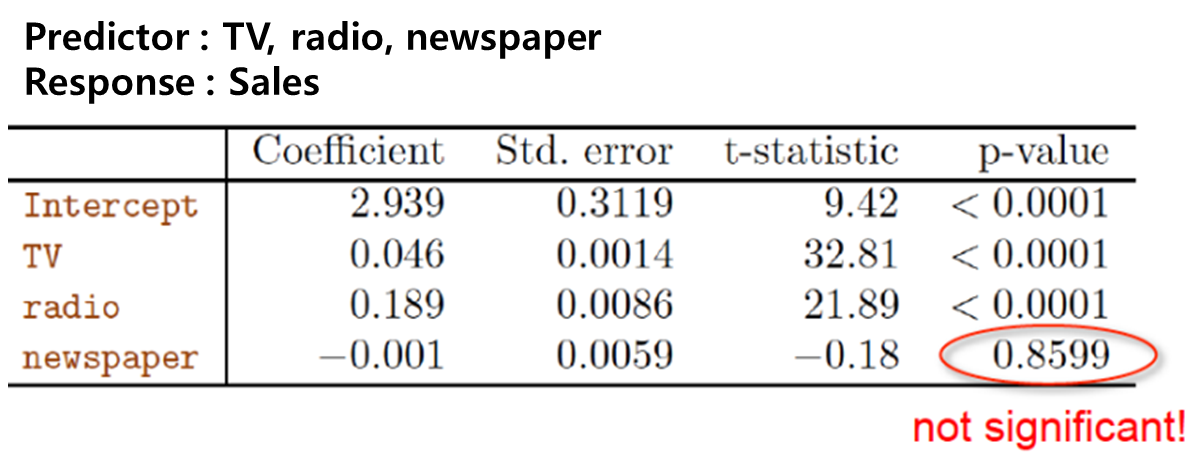
• 예제2 (광고)
  : Coefficient(계수) -> 입력변수와 출력변수 사이의 관계, 0에 가까울수록 영향x
  : Std.error(표준 오차) -> 계수 추정치의 정확성(표준 편차), 작을 수록 좋음
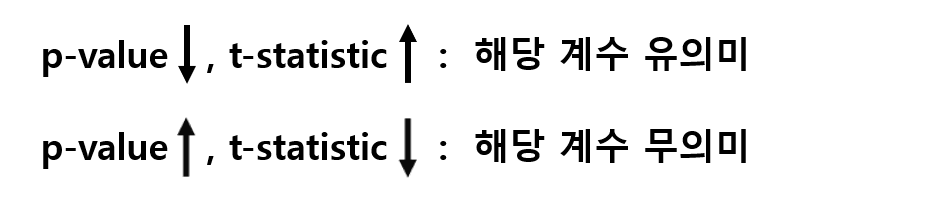
  : t-statistic(t통계량) -> 계수 추정치와 표준 오차 비교
  : p-value (p-값)
  : F-statistic(f통계량) -> 선형 회귀 모델의 전체적인 적합도 평가

<다른 고려사항들..>
06. 질적 예측자 (Qualitative Predictors)
07. 상호 작용 효과 (Interaction effects)
08. 비선형 연관성 (Nonlinear relationship)