F-score에서 $\beta$의 역할

Recall과 Precision의 조화평균인 F-score에서는 $\beta$ 값을 통해, Recall과 Precision 중 어떤 값을 더 중요하게 관찰할 것인지를 결정한다.

---

조금 더 구체적으로,
$\beta>1$인 경우 Recall을 더 중요하게,
$\beta<1$인 경우 Precision을 더 중요하게 여기는 F-score가 된다는 것 또한 익히 알려져 있다.

그러나, 왜 $\beta$값에 따라, 위와 같은 로직으로 F-score가 작동하는지에 대한 친절한 설명은 찾기 어려워서 글을 쓰기 시작했다.

먼저, F-score의 근간이 되는 조화 평균의 개념을 간단히 살펴보고,
이를 F-score와 연결지어, $\beta$값에 따른 F-score의 변화를 이해할 것이다.
(아무런 이해 없이, 단순히 암기하면 까먹는다 무조건)

---

1. 조화 평균

F-score는 다들 알고 있는 것처럼 Recall과 Precision으로 구성된 조화 평균이다.

그러므로, 조화 평균의 개념을 먼저 파악하는 것이 중요할 듯 싶다.

정의: 주어진 수들의 역수의 산술평균의 역수

• 처음 들으면 조금 곤란한 워딩의 연속인데, 천천히 읽어보면 그리 어려운 개념은 아니다.

---

예시

주어진 $n$개의 수 $a_1, a_2, ..., a_n$이 있다고 하자.

다시 돌아가서 조화 평균의 정의를 읽어보면, ‘주어진 수들의 역수의 산수평균의 역수’

1. 우리는 여기서, 주어진 수들의 역수까지만 먼저 보자
   • 주어진 수들의 역수: $\frac{1}{a_1},\frac{1}{a_2},...,\frac{1}{a_n}$
2. 그럼 이제 정의에 조금 더 가까워져 보자. ‘주어진 수들의 역수의 산수평균’
   • 주어진 수들의 역수의 산수평균: $(\frac{1}{a_1}+\frac{1}{a_2}+ \cdots+\frac{1}{a_n})/n$
3. 마지막이다. ‘주어진 수들의 역수의 산수평균의 역수’
   • $n/(\frac{1}{a_1}+\frac{1}{a_2}+ \cdots+\frac{1}{a_n})$

---

사실 크게 봐야 와 닿는다.

조화 평균의 수식

---

2. F-score에 적용

이제 위에서 $a_i$라고 칭했던 주어진 수가 Precision과 Recall로 바뀐 것 뿐이다.

F-score: 예시 1

주어진 수: $\text{Precision, Recall}$

여기서, 분모﹒분자에 $\text{Precision}$과 $\text{Recall}$을 곱하면 아래와 같아진다.

→ 우리가 알던 F1-score 식이다.

---

F-score: 예시 2 (확장)

방금의 예시에서는 ‘주어진 수’가 $\text{Precision}$, $\text{Recall}$ 각각 1개였다.

이번 예시에서는 $\text{Precision}$이 1개, $\text{Recall}$이 $\beta^2$개라고 해보자.(즉, $\text{Recall}$에 $\beta^2$만큼의 가중치를 부여해보자)

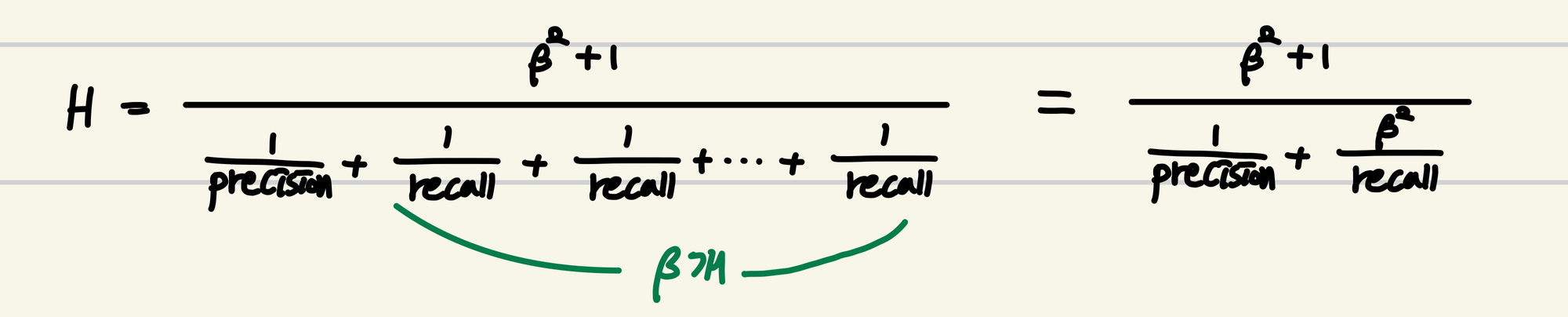
여기서도, 분모﹒분자에 $\text{Precision}$과 $\text{Recall}$을 곱하면 아래와 같다.

---

직관과 연결

$\text{Recall}$에 $\beta^2$만큼의 가중치를 부여한 식이 위와 같을 때, $\beta^2$의 값을 바꿔가며 생각해보자.

다시 한 번 말하자면, 우리는 $\text{Precision}$이 1개, $\text{Recall}$이 $\beta^2$개에 대한 조화 평균을 구한 것이다.

CASE 1: $\beta>1$

e.g., $\beta = 2$인 경우

• 즉, $\text{Precision}$이 1개, $\text{Recall}$이 $2^2=4$개인 경우다. $\text{Recall}$을 더 중점적으로 보는 조화 평균 값이라는 건 이제 너무나도 직관적으로 알 수 있다.
  

---

CASE 2: $\beta<1$

e.g., $\beta = 0.1$인 경우

• 즉, $\text{Precision}$이 1개, $\text{Recall}$이 $(0.1)^2=0.01$개인 경우다. 여기서는 $\text{Precision}$을 더 중점적으로 보는 조화 평균 값이라는 것 또한 너무나도 직관적.
  

---

CASE 3: $\beta=1$

e.g., $\beta = 1$인 경우

• 즉, $\text{Precision}$이 1개, $\text{Recall}$도 $1$개인 경우다. 여기서는 $\text{Precision}$과 $\text{Recall}$을 동등하게 구한 조화 평균 값이라는 것 또한 너무나도 직관적.
  

---

끝.