Overfitting과 Underfitting, 그리고 Ridge Regression

1. Dataset Split의 필요성

모델의 overfitting과 underfitting을 설명하기 전에, 모델의 학습 과정을 먼저 살펴보자.

모델 학습 시 일반적으로 Dataset을 나눌 텐데, 이렇게 나눈 Train, Validation, Test Set 각각의 존재 이유를 먼저 살펴보고 넘어가자.

1.1 Train, Validation, Test Set의 정의

• Train Set: 모델을 학습시키기 위한 데이터셋
• Validation Set: 학습된 모델의 하이퍼파라미터 튜닝 및 성능 평가를 위한 데이터셋
  • 모델의 일반화 성능 평가
  • 과적합을 방지하기 위해 사용
• Test Set: 최종적으로 모델의 성능을 평가하기 위한 데이터셋
  • 학습 및 튜닝 과정에서 전혀 사용 X
  • 모델의 실제 예측 성능을 평가하는 데 사용

1.2 데이터셋을 나누는 이유

우리가 수능을 본다고 가정해보자. 우리도 시험을 보기 전까지는 실제 시험지가 어떻게 생겼는지 알 수 없다. (알면 잡혀간다)

• 물론 미리 알게 된다면, 답을 외운 채로 그 시험 한 번은 잘 보겠지만 그렇게 똑똑해지지는 않을 거다. (즉, 문제가 조금만 바뀌어도 풀 수 없을 것이다.)

모델도 마찬가지다. 이 녀석이 수능 시험지인 Test set을 학습 단계에서 미리 훔쳐 보게 되면, 당장의 시험은 잘 보겠지만 시험지가 조금만 바뀌어도 사경을 헤맬 거다. (즉, 일반화 성능이 엉망일 것이다.)

또, 우리가 열심히 공부만 한다고 시험을 항상 잘 보진 않는다.

중간 중간 ‘실전 경험’을 늘리기 위해서 모의고사를 보곤 한다. 또, 이 모의고사 점수를 통해서 내가 볼 수능 점수를 대략적으로 가늠하기도 한다.

이게 Validation set이 되겠다.

정리하면 이렇다.

모델은 우선 Validation set이라는 모의고사를 잘 보기 위해, Train set을 이런 저런 방법으로 열심히 공부를 하고 시험장에 나간다.

그리고 Test set이라는 수능을 보고 우리에게 평가를 받는다.

• 모델의 평가를 위해 고안된 지표가 바로 Metric이다.
  • e.g., Accuracy, Precision, Recall 등이 있겠다.

우리가 모의고사를 잘 보기 위해, 공부법을 다양하게 시도해보는 것이 Hyperparameter Tuning이 될 것이고,

공부를 많이 할 수록 수능을 잘 볼 확률이 높은 만큼, 데이터셋의 크기는 클 수록 좋을 것이다.

💡 한 마디로 정리하자면,
Train set은 학습을 위해 존재하고,
Validation set은 하이퍼파라미터 튜닝을 위해 존재하고,
Test set은 평가를 위해 존재한다.

---

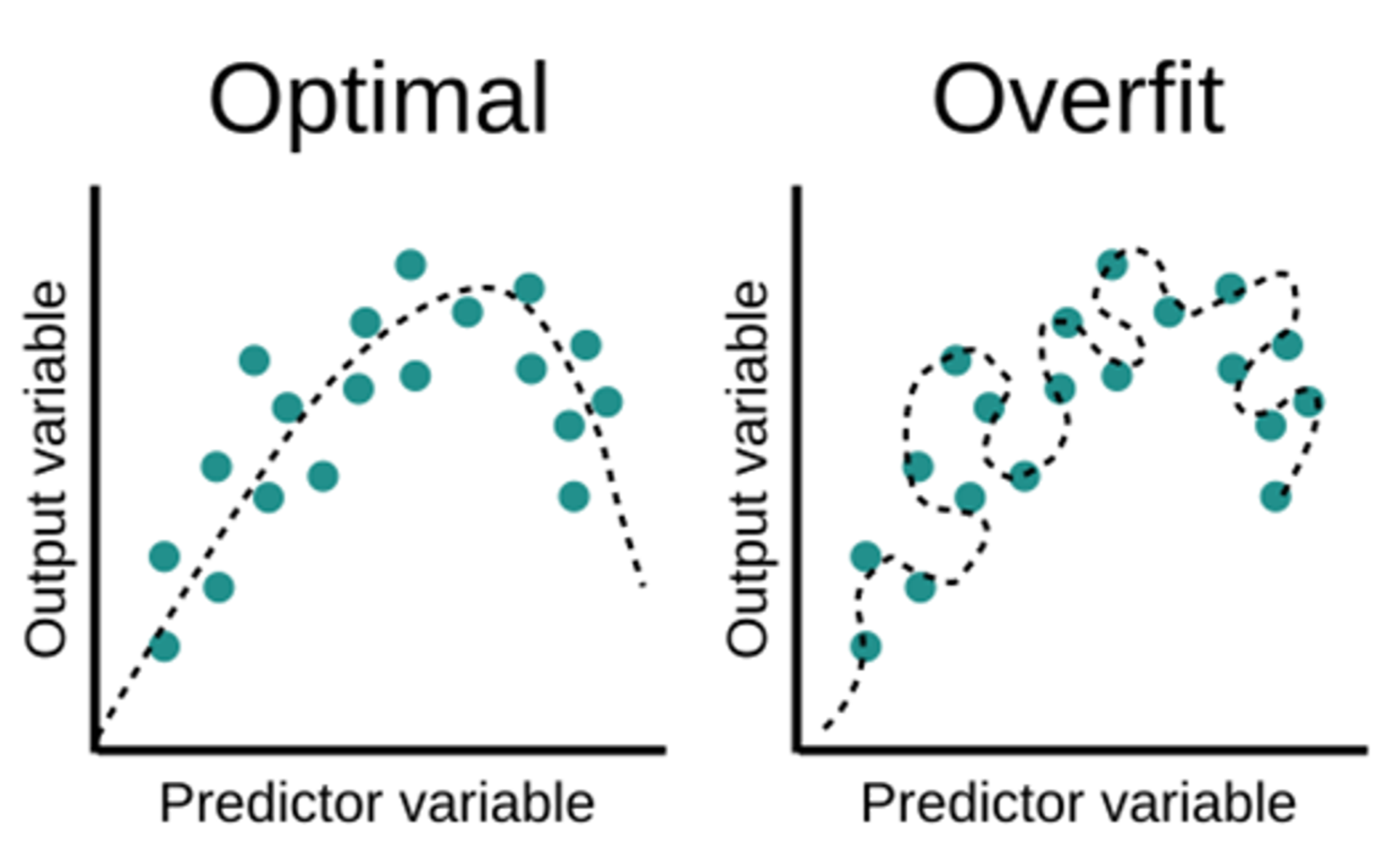
과적합(Overfitting)

Overfitting된 모델은 책(Train set)만 달달 외워서, 본 시험(Test set)을 못 보는 학생을 생각하면 직관적이겠다.

Overfitting은 모델이 학습 데이터의 노이즈나 세부 사항까지 학습하게 되는 현상이다.

→ 이로 인해 새로운 데이터에 대해서는 일반화가 잘 되지 않아서 성능이 떨어진다.

원인:

• 너무 복잡한 모델 사용 (e.g., 깊은 신경망, 많은 parameter)
  
  
• Train data의 양 부족
• Train data에 노이즈가 많은 경우

결과:

• Train data에 대해서는 높은 성능을 보이지만, Validation data나 새로운 데이터에 대해서는 낮은 성능을 보임
• 모델의 learning curve에서 train loss는 낮으나 valid loss가 높은 경우
  

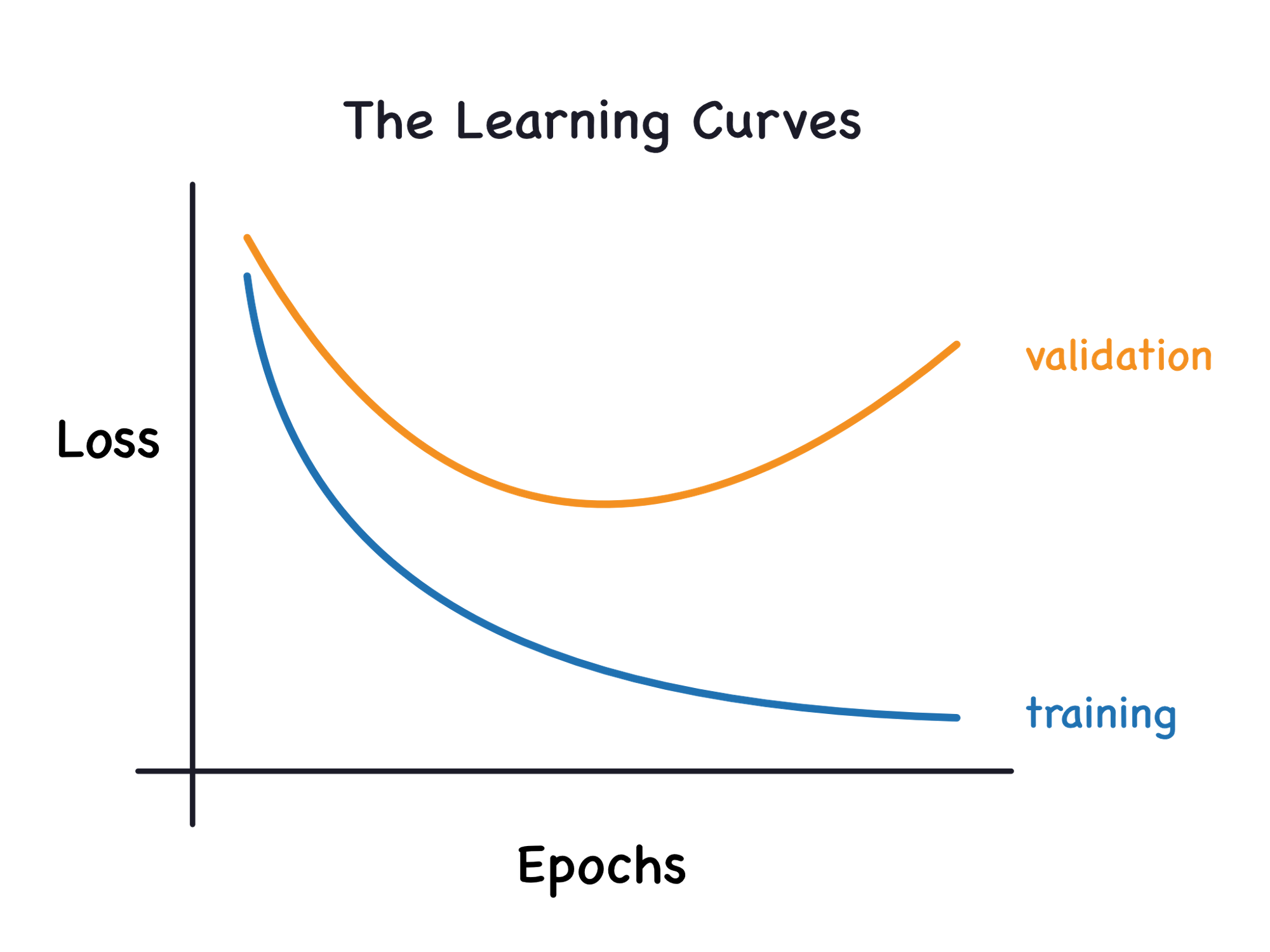
방지 방법:

1. 더 많은 데이터 수집:

   • 더 많은 데이터를 수집함으로써 모델이 노이즈에 덜 민감해지도록 함.

2. Regularization:

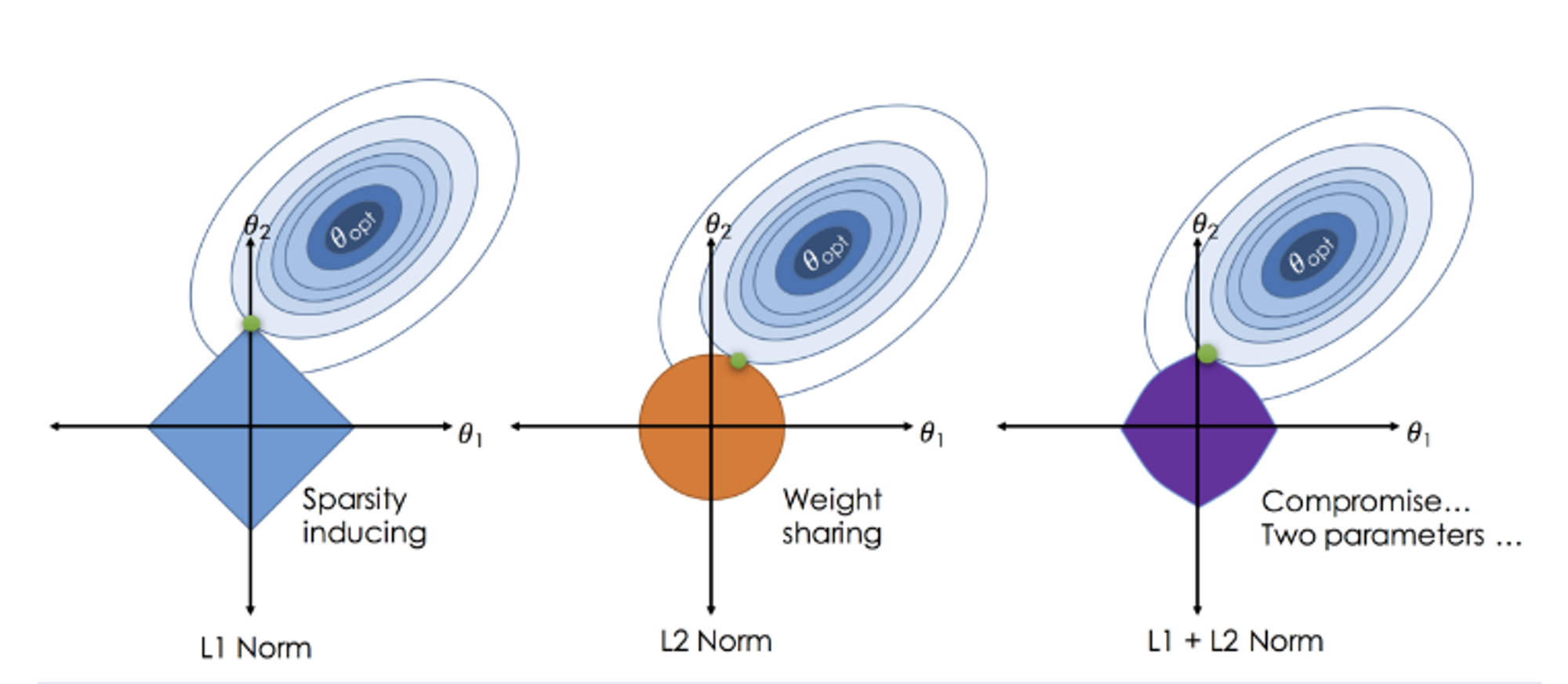
   • L1, L2 Regularization을 통해 모델의 복잡도를 줄임.
   • L1 Regularization은 일부 parameter를 0으로 만들어 변수 선택 효과를 줌.
   • L2 Regularization은 모든 parameter를 작게 만들어 overfitting을 방지

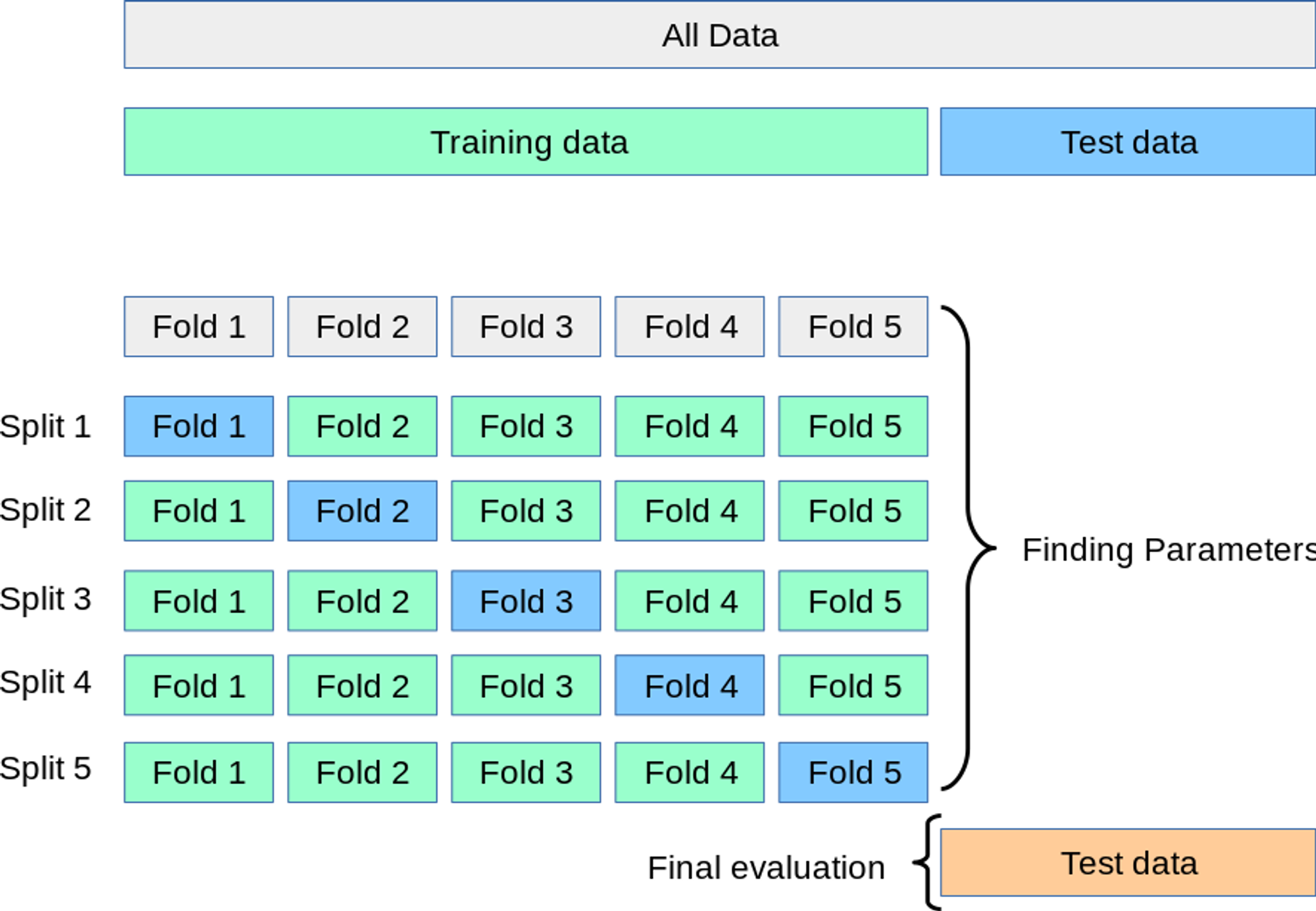
3. Cross-Validation:

   

   • 데이터셋을 여러 부분으로 나누어 각 부분에 대해 학습 및 평가를 반복함으로써 모델의 일반화 성능을 평가.

4. 앙상블 기법 (Ensemble Methods):

   • 여러 모델을 결합하여 성능 향상 & overfitting 감소
   • e.g., 배깅(Bagging), 부스팅(Boosting) 등

---

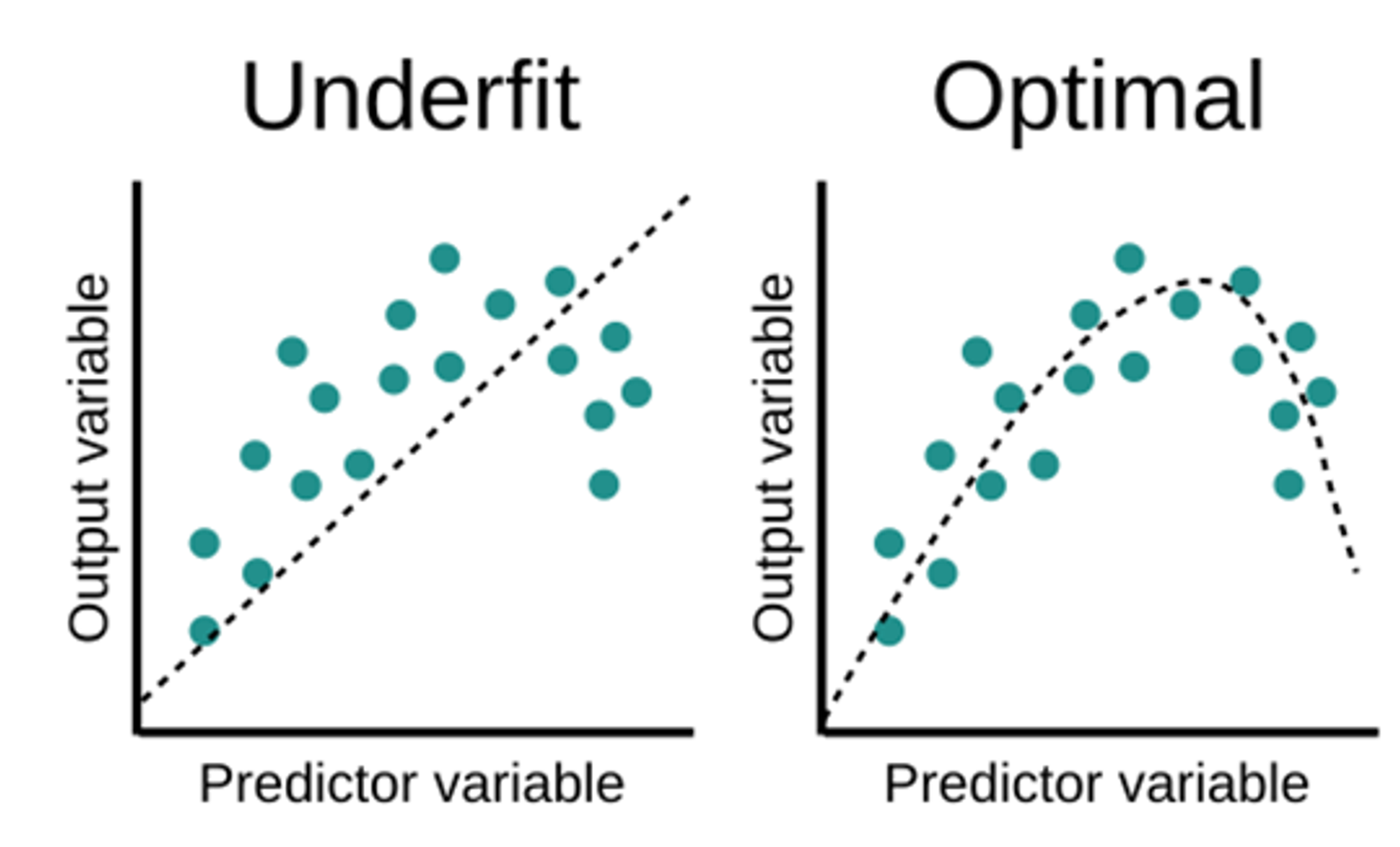
Underfitting

모델이 학습 데이터의 패턴을 충분히 학습하지 못한 상태

Train set과 새로운 데이터 모두에 대해 성능 ↓

원인:

• 모델이 너무 단순한 경우 (e.g., 선형 모델을 복잡한 데이터에 사용한 경우)
• 학습 데이터가 충분하지 않거나, 모델의 Feature가 적절하지 않은 경우

결과:

• Train set, Valid set 모두에서 낮은 성능
• 모델의 learning curve에서 train loss & valid loss 모두 높은 경우

방지 방법:

1. 더 복잡한 모델 사용:
   • 더 복잡한 모델을 사용하여 데이터의 패턴을 잘 학습할 수 있도록 함.
2. 더 많은 feature 추가
3. Hyperparameter Tuning
4. 데이터 전처리 (Data Preprocessing)

Bias-Variance Tradeoff

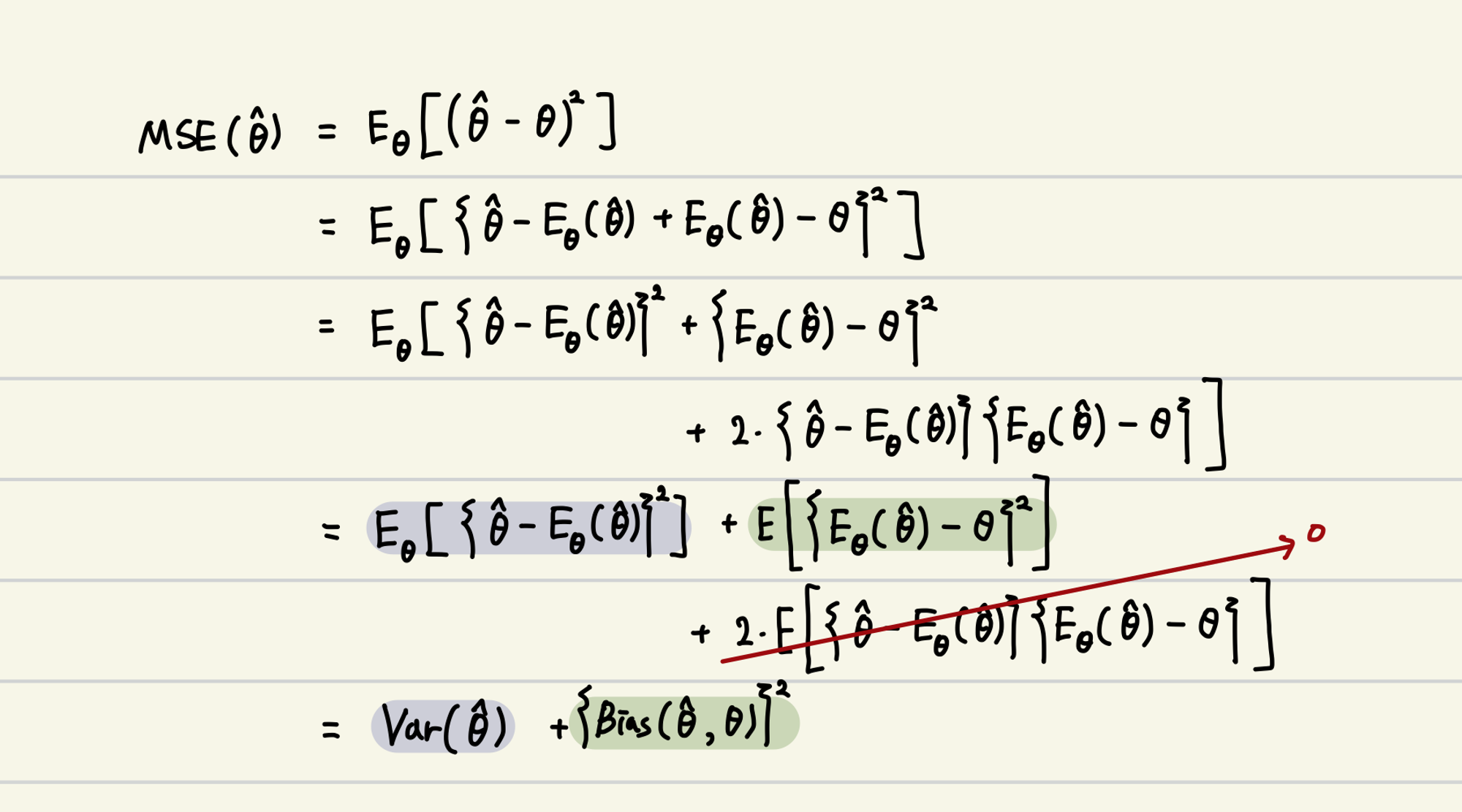
💡 모델을 복잡하게 하면, Variance ↑
모델을 단순하게 하면, Bias ↑
→ Dilemma

그런데, 일반 선형 회귀는 Unbiasedness에 Focus

→ Bias를 줄이되, Variance는 늘어나는 형태로 Model이 fitting

Regularization의 의도

: Unbiasedness는 조금 포기하더라도, Variance를 잡자. (즉, overfitting을 잡자)

Ridge Regression

이러한 Bias-Variance Tradeoff로 인해,

모델은 복잡하게 하되, Train data의 패턴을 덜 학습하도록 (즉, 일반화 성능을 잃지 않도록) 만들어보자.

= Regularization을 해보자

Regularization?

간혹 정규화, 정칙화로도 불리는데, 이러한 표현은 개인적으로 정말 와 닿지가 않는다.

그나마, ‘규제’라는 표현이 나은듯 싶다.

모델 학습에 쓰이는 Cost function에 Penalty를 부여해서 (즉, 규제를 더해서) overfitting을 방지하는 데에 의의가 있는 거니까.

Ridge Regression 소개

Regression 문제에서 Regularization 관련 항이 포함된 모델로는 Ridge, Lasso, Elastic Net 등이 있다.

1. Ridge regression

   : Cost function에 L2 norm을 추가하여 Regularization을 진행한 regression model

2. Lasso regression

   : Cost function에 L1 norm을 추가하여 Regularization을 진행한 regression model

3. Elastic Net regression

   : Ridge, Lasso의 절충안

💡 간혹 Ridge와 Lasso 각각이 누가 L1-norm이었고, L2-norm이었는지 헷갈릴 수 있는데,
Lasso에서 ‘a’가 absolute을 의미한다. (이것만 기억하면 절대 안 까먹는다)
Ridge는 산등성이, 능선을 의미한다는데.. 뭐 그렇다

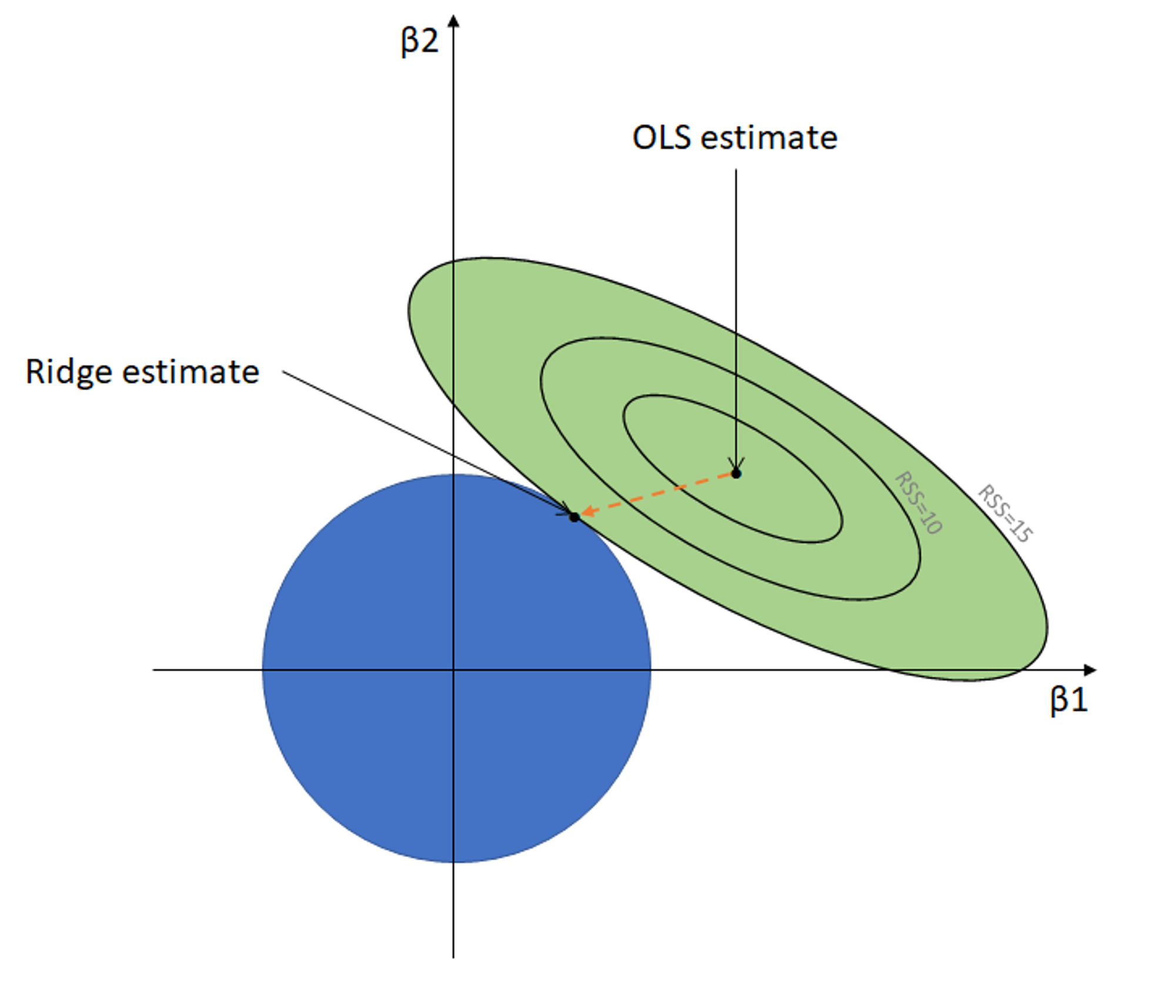
Ridge Regression Deep Dive

일반 선형 회귀 추정식

Ridge 회귀 추정식

• 빨간색 Penalty term

  : parameter의 값들이 일정 수준 이상 커지지 않도록 Regularization

  • $\lambda$가 Regularization의 정도를 조절 (Hyperparameter)

• $\lambda$가 매우 큰 경우

  : 대부분의 $\beta_j$가 0에 가까운 값을 갖게 됨
  

• $\lambda$가 매우 작은 경우

  : Regularization의 의미가 없어진다. (즉 overfitting을 막지 못함)
  

• Penalty term의 다른 표현 방식

  $\lambda$가 아닌 다른 방식으로도 penalty term을 표현할 수 있다.

  $\sum_{j=1}^{p}\beta_j ^2 \leq t$

MSE의 contour plot

MSE가 등고선 플롯이 되는 이유

1. MSE의 정의

우리는 일반 선형 회귀의 평균 제곱 오차(MSE)를 다음과 같이 정의합니다:

2. 제곱 항 전개

위의 식을 전개하면 다음과 같다:

3. 각 항의 세부 전개

4. 최종 정리

이 식을 간단하게 표현하면:

5. 이차 함수 판별식

• where
  • $A = \sum_{i=1}^{n} x_{i1}^2$
  • $C = \sum_{i=1}^{n} x_{i2}^2$
  • $B = 2 \sum_{i=1}^{n} x_{i1} x_{i2}$
  • $D = -2 \sum_{i=1}^{n} y_i x_{i1}$
  • $E = -2 \sum_{i=1}^{n} y_i x_{i2}$
  • $F = \sum_{i=1}^{n} y_i^2$

6. 판별식 계산

위의 MSE 식은 $\beta_1$과 $\beta_2$에 대한 이차 함수의 일반적인 형태

다음으로, 이차 곡선의 형태를 결정하는 판별식 $\Delta = B^2 - 4AC$를 계산합니다.

이를 다시 정리하면:

7. Cauchy–Schwarz inequality 적용

Cauchy–Schwarz inequality

이 부등식을 $a_i = x_{i1},\ b_i = x_{i2}$에 적용하면:

따라서,

이로 인해,

즉, $\beta_1$, $\beta_2$에 대한 MSE의 contour plot은 타원(ellipse)형 곡선

---

Lasso, Elastic Net도 위와 같은 맥락

단지, penalty term의 방식만 다를 뿐

---