[Paper Review] Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

2019년 ACL에서 발표한 논문입니다.

0. Abstract

Transformer는 longer-term dependency의 학습에 잠재력이 있지만, 고정된 길이의 문맥만을 학습하기 때문에 한계가 있습니다. 따라서 본 논문에서는 고정된 길이를 넘어 의존성을 학습할 수 있는 Transformer-XL을 소개하고자 합니다. longer-term dependency를 포착하고 context fragmentation을 해결하는 것이 주된 목적입니다.

결과적으로 Transformer-XL은 RNNs보다 80%, vanilla Transformer보다 450% 더 길게 의존성을 학습했고, 짧은 문장과 긴 문장 모두에서 더 나은 성능을 보여줬습니다.

1. Introduction

Language Modeling은 비지도 사전학습 적용뿐만 아니라 long-term dependency를 모델링 해야 하는 중요한 문제입니다. 하지만 모델이 sequence 데이터에서 long-term dependency를 모델링할 수 있도록 하는 것은 계속해서 도전과제였습니다.

RNN과 LSTM은 좋은 성능을 보여줬기에 널리 사용되었던 언어 모델입니다. 하지만 RNN은 gradient vanishing과 explosion 문제로 최적화하기 어려웠고, gate를 도입한 LSTM과 gradient clipping 기술을 통해 어느정도 완화했지만 문제를 완전히 해소하기엔 부족했습니다. 이후 멀리 떨어진 두 단어 쌍 사이를 직접적으로 연결하는 Attention Mechansim이 등장하고 Transformer가 등장하면서 최적화가 용이해지고 long-term dependency를 학습할 수 있게 되었습니다.

이후 Transformer의 깊게 쌓은 구조를 가진 character-level 언어모델이 제안되었고, 엄청난 차이로 LSTM의 성능을 능가했습니다. 하지만 이것은 연속된 문장 시퀀스를 고정된 길이의 여러 세그먼트로 분리해서 모델에 입력해야 했고, 세그먼트간 정보를 전달하지 않는다는 문제가 있습니다. 고정된 길이의 세그먼트는 해당 길이 만큼의 context만 잡아낼 수 있고, 결과적으로 context길이 이상의 long-term dependency를 포착할 수 없습니다.

또한, 고정된 길이의 세그먼트는 문장 혹은 의미 간의 구조를 고려하지 않고 단지 마침표, 물음표 등의 기호를 기준으로 분리하므로 context fragmentation이 발생합니다. 그리고 매 세그먼트 앞단의 토큰을 예측할 때 이전 정보의 양이 부족해 모델의 최적화가 비효율적이고 성능이 저하됩니다.

앞서 언급한 문제를 해결하기 위해, 본 논문에서는 Transformer-XL을 제안합니다. 각각의 segment마다 hidden state를 처음부터 계산하는 대신, 이전 세그먼트의 hidden state를 재사용해 세그먼트 단위로 Recurrent하게 연결하는 아이디어입니다. 이를 통해 long-term dependency 모델링이 가능해지고 context fragment 문제도 해결할 수 있게 됩니다. 그리고 이 아이디어의 효과적인 적용을 위해 Relative positional encoding을 도입합니다.

2. Related Work

언어 모델링 분야에는 지난 몇년간 상당한 발전을 보여주었습니다. 더 긴 범위의 context를 캡처하기 위해 노력해왔고, 여러 분야에서 사용했습니다. 다만, 일반적인 sequence 모델링에서 long-term dependency의 모델링 성능을 향상시키는 일에 대해서는 항상 거론되는 과제였습니다.

LSTM은 다양한 task에서 사용되었기 때문에, LSTM 아키텍쳐에서 long-term dependency를 더 잘 포착하기 위해 vanishing gradient를 완화하는 여러 연구가 진행되었습니다. 한편, 본 연구는 Transformer 아키텍쳐에 기반하였고, longer-term dependency의 모델링 능력 향상을 보여주었습니다.

3. Model

문장이 $x=(x_1,...,x_T)$와 같은 토큰으로 이뤄졌다고 가정해보겠습니다. 언어 모델링은 현재 시점 t를 기준으로 이전 토큰 $x\_{<t}$을 가지고 현재 시점 토큰 $x\_t$를 예측하기 위해 결합확률 $P(x)$의 분포를 추정하는 것입니다. 즉 $P(x)=\Pi_t P(x_t \ | \ x_{<t})$와 같이 추정하며, 이것은 auto-regressive한 방식입니다.

이러한 방식은 결국 각 요소의 조건부 분포를 추정하는 문제이고, 저자들은 Neural Network를 이용해 이러한 방식을 모델링하고자 했습니다. Neural Network를 이용한 방법 다음과 같이 진행됩니다.

먼저, 이전 토큰 $x_{<t}$를 고정된 길이의 벡터로 만들고, 이 벡터와 word embedding을 곱하여 logit을 얻습니다. 이후 logit에 softmax 함수를 적용해 다음 토큰에 대한 확률 분포를 만들어냅니다.

3.1 Vanilla Transformer Language Models

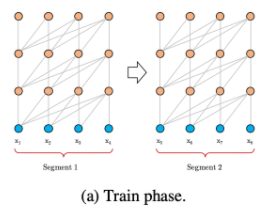
그래서 Al-Rfou et al. (2018)에서는 모델의 학습을 위해 전체 문장을 처리 가능한 크기의 세그먼트로 나눈뒤, 오직 각각의 세그먼트 안에서만 모델을 학습시키는 방법을 사용했습니다.

하지만 세그먼트간 정보가 흐르지 못해 이전 세그먼트로부터의 모든 문맥적 정보는 무시되는 치명적인 단점이 있습니다. 이러한 이유로 모델이 파악할 수 있는 최대 dependency가 세그먼트의 길이에 한정되고, 이것은 self-attention 메커니즘의 장점을 온전히 사용할 수 없다고 할 수 있습니다. 또한, 패딩을 사용해 문장 혹은 의미의 경계를 구분할 수 있지만 실제로는 효율성의 문제로 문장을 입력하고 단순히 고정된 길이로 분할하는게 표준 관행이었고, 이는 context fragmentation를 유발하는 문제가 존재합니다.

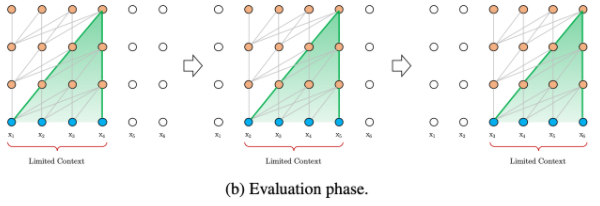
vanilla Transformer 모델이 예측을 수행하는 방식을 살펴보면, 학습에서와 같은 길이의 세그먼트에서 마지막 위치의 한개 토큰을 예측합니다. 이후의 세그먼트들도 오른쪽으로 한칸씩 움직이는 sliding window 방식으로 각 토큰을 예측합니다. 이 방식은 고정된 세그먼트 길이만큼의 context를 활용하지만, 훈련에서 발생하는 context fragmentation 문제를 완화해줄 순 있습니다. 하지만 이러한 과정은 많은 계산량을 요구합니다.

3.2 Segment-Level Recurrence with State Reuse

본 논문에서는 Recurrence 매커니즘을 도입해 vanilla Transformer의 문제를 완화하고자 합니다.

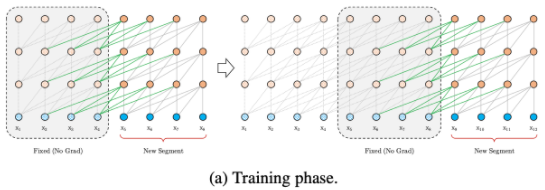
Recurrence 매커니즘을 적용하였을때 학습과정을 살펴보겠습니다. 세그먼트 단위로 학습을 수행하는건 이전 모델과 동일합니다. 다만, 여기서는 이전 세그먼트에서 계산된 hidden state 값을 다음 세그먼트에서 이를 재사용할 수 있도록 고정하고 저장하여, 이전 세그먼트의 정보들을 전달받을 수 있도록 해주는 것이죠. 이를 통해 이전의 정보들을 이용할 수 있게 되면서 longer-term dependency 능력이 향상되고 context fragmentation 문제가 완화됩니다.

입력된 시퀀스 토큰이 $s_\tau = [x_{\tau , 1}, ... , x_{\tau , L}]$, $s_{\tau + 1} = [x_{\tau +1 , 1}, ... , x_{\tau +1 , L}]$와 같이 길이가 L인 두개의 세그먼트로 나눠져 있다고 가정해보겠습니다. 이때 각 세그먼트를 학습은 이전 세그먼트의 정보를 재사용하기 위해 아래와 같은 수식으로 계산하게 됩니다.

$\tilde h^{n-1} _ {\tau+1}= [SG(h^{n-1}_{\tau}) \circ h^{n-1}_{\tau+1}]$

현재시점 세그먼트의 hidden state와 이전 세그먼트 hidden state를 concat하고, 이것은 n번째 layer에서 입력으로 사용됩니다. 단, 이때 이전 세그먼트 hidden state의 파라미터는 고정해두고 현재 파라미터만 학습합니다.

$q^n_{\tau+1}, k^n_{\tau+1}, v^n_{\tau+1} = h^{n-1}_{\tau+1}W_q^\top, \tilde h^{n-1}_{\tau+1}W_k^\top, \tilde h^{n-1}_{\tau+1}W_v^\top$

예측할 토큰의 self-attention에 사용될 Query, Key, Value 벡터를 만듭니다. 여기서 예측할 토큰이 속하는 현재 세그먼트($s_{\tau+1}$)의 hidden state를 통해 query를 구하고, 이전 세그먼트의 hidden state값을 활용해 key와 value 값을 구합니다.

$h^n_{\tau +1} = TransformerLayer(q^n_{\tau+1}, k^n_{\tau+1}, v^n_{\tau+1})$

이후 위의 과정으로 구한 query, key, value 값으로 Transformer의 self-attention을 수행하여 현재 세그먼트의 hidden state를 얻습니다.

Fig. 3은 $h_{\tau+1}^n$을 얻기 위한 일련의 과정을 보여주는데, 초록색 선을 통해 이전 세그먼트로부터 hidden state 값을 재사용하는 것을 확인할 수 있습니다.

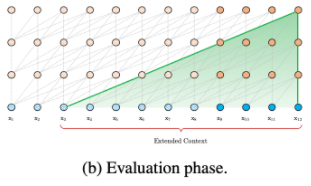
위에서 살펴보았듯이 두 세그먼트 사이에 recurrence 메커니즘을 적용하였는데, 이처럼 recurrence 메커니즘은 세그먼트 단위로 적용하게 됩니다. 이것은 두개의 세그먼트를 넘어 더 긴 여러 세그먼트 사이에서도 context를 잡아낼 수 있게 됩니다. 하지만 $h^n_{\tau+1}$와 $h^{n-1}_\tau$ 간의 의존관계는 세그먼트 당 하나의 layer씩 밀리기 때문에, dependency의 최대 길이는 [Layer 수 x 세그먼트 길이]가 됩니다(그림에서는 3x4=12 길이만큼).

또다른 장점으로는 평가시에 속도가 vanilla Transformer 대비 최대 1800배 빨라집니다. Vanilla Transformer에서는 세그멘트를 한칸씩 옆으로 옮기면서 매번 hidden state를 계산하는 반면, 제안된 방법에서는 이전 세그먼트의 정보를 재사용하기 때문입니다. 또한, GPU 자원의 한도 내에서 이전 세그먼트의 길이를 더 길게 가져가 의존성을 더 길게 가질 수 있습니다.

3.3 Relative Positional Encodings

앞서 제안한 방법을 사용하기 위해선 ‘세그먼트 사이에 정보를 재사용할때 어떻게 position 정보를 일관되게 유지할 것인지’에 대한 문제를 해결해야 합니다. 기존의 Transformer에서는 토큰의 embedding을 word embedding과 절대적인 positional encoding의 각 요소의 합으로 나타냅니다.

$h_{\tau+1}=f(h_\tau, E_{s_{\tau+1}}+U_{1:L})$

$h_{\tau}=f(h_{\tau-1}, E_{s_{\tau}}+U_{1:L})$

이를 recurrence 매커니즘에 적용하면 hidden state 값은 위의 수식과 같이 나태낼 수 있습니다. ($E$는 word embedding을 $U$는 positional encoding을 의미). 하지만 수식에서 보듯이 각 세그먼트의 hidden state를 계산하는데 같은 위치 정보를 사용하고 있습니다. 그렇기 때문에 모델은 시퀀스내에 $x_{\tau, j}$와 $x_{\tau+1,j}$ 사이 위치적인 차이를 구분하기 어려워지게 됩니다.

생각해보면 Positional encoding은 모델의 각 토큰들에 위치정보를 부여해 서로 attention해야 할 토큰을 구분해주는 역할을 합니다. 이를 위해 기존 Transformer에서는 초기 embedding에 포함시키는 방식이었는데, 이 위치정보는 실질적으로 위치정보가 사용되는 attention score를 구하는 과정에 직접 포함시켜 동일한 목적을 수행할 수 있습니다. 사실 각 토큰의 query, key 벡터 사이의 유사도를 계산하는데, 토큰 사이의 절대적인 위치 정보보다 상대적인 거리를 아는 것이 핵심이기 때문이죠.

따라서 본 논문에서는 Relative Positional Encoding 방식을 제안하였는데, 두 토큰 사이의 상대적인 거리를 나타내는 $R\_i$를 인코딩하는 것이 핵심입니다. 기존의 방식과 Relative positional encoding이 적용된 방식을 비교해보겠습니다.

$A_{ij}^{abs}= (E_{x_i}^\top U_i^\top) W_q^\top ((E_{x_i}^\top U_j^\top)W_k ^\top)^\top$

$A_{ij}^{abs}= E_{x_i}^\top W_q^\top W_k E_{x_j} + E_{x_i}^\top W_q^\top W_k U_j + U_i^\top W_q^\top W_k E_{x_j} + U_i^\top W_q^\top W_k U_j$

먼저 기존 Transformer에서 동일 세그먼트 내 i번째 query와 j번째 key 토큰 사이의 attention score는 다음과 같이 계산됩니다.

$A_{ij}^{rel}= E_{x_i}^\top W_q^\top W_{k,E} E_{x_j} + E_{x_i}^\top W_q^\top W_{k,R} R_{i-j} + u^\top W_{k,E} E_{x_j} + v^\top W_{k,R} R_{i-j}$

그리고 새롭게 제안한 relative positional encoding를 적용한 attention score의 연산 과정은 다음과 같습니다.

두 식 사이의 차이는 이렇습니다.

• 2, 4번째 항에서 Key 벡터의 Absoulte positional embedding $U_i$, $U_j$를 Relative한 $R_{i-j}$로 대체했습니다. 토큰사이 상대적인 거리의 encoding입니다.
• Query 벡터는 모든 위치에서 동일한 값을 가지기 때문에 일정한 bias로 볼 수 있습니다. 따라서 3번째 항의 $U_i^\top W_q^\top$를 $u \in R^d$로 대체합니다. 또한, 같은 이유로 4번째 항의 $U_i^\top W_q^\top$도 $v \in R^d$로 대체합니다.
• 1, 3번째 항을 묶어서 보면 $(E_{x_i}^\top W_q^\top +u^\top) W_{k,E} E_{x_j}$로 나타내어 집니다.
• 2, 4번째 항을 묶어서 보면 $(E_{x_i}^\top W_q^\top +v^\top) W_{k,R} R_{i-j}$로 나타내어 집니다.
• 마지막으로 $W_k$를 $W_{k,E}$, $W_{k,R}$로 나누는데, 각 항에서 Key 값에 대한 가중치를 컨텐츠 기반, 위치 기반으로 나누어 key 벡터를 구성합니다. 각 항에서 $W_k$의 역할이 구분되는 것을 확인할 수 있습니다.
  • $A_{ij}^{rel}= (E_{x_i}^\top W_q^\top + u^\top)W_{k,E} E_{x_j} +( E_{x_i}^\top W_q^\top +v^\top) W_{k,R} R_{i-j}$

각 항의 직관적인 의미는 이렇습니다.

• 첫번째 항은 컨텐츠 기반의 전달
• 두번째 항은 컨텐츠에 의존한 positional bias 파악
• 세번째 항은 글로벌 컨텐츠 bias
• 마지막 항은 글로벌 위치 bias

특히 상대적 위치 인코딩을 수행할 때는 두 토큰의 상대적인 위치를 sin함수와 cos함수를 사용해 인코딩하게 됩니다. 예를들어 상대적인 위치 인코딩을 512까지 할 수 있고, 이때 20개의 토큰을 입력받아 상대적이 위치 인코딩을 수행한다고 가정해보겠습니다. 먼저 sin함수와 cos함수를 합쳐 $R$ matrix를 구합니다. matrix는 다음과 같이 시각적으로 표현할 수 있는데, 왼쪽이 sin함수를 통해 나온 값이고 오른쪽이 cos함수를 통해 나온 값입니다. 각 행이 상대적인 위치 차이에 쓰일 벡터값입니다.

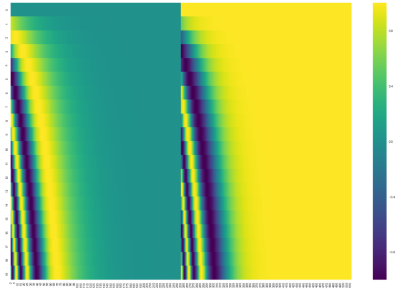
모델은 이 matrix를 look up table로 사용해, 각 토큰의 상대적인 거리 차이만큼에 해당하는 값을 matrix의 행에서 가져와 인코딩하는 것입니다.

정리해보면 제안된 Relative positional embedding과 Recurrence 메커니즘은 실질적으로 attention score를 구할 때 반영되고, 나머지 계산 과정은 기존의 Transformer와 같습니다.

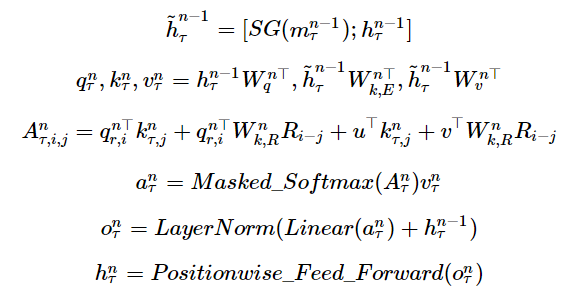
단일 attention head로 구성된 $n$개의 layer의 Transformer-XL를 가정했을때, 계산 과정은 위와 같습니다. 가장 초기 입력은 $h^0_\tau := E_{s_\tau}$로 단어 임베딩 값으로만 구성됩니다. 또한, n-th layer별로 상대위치 값($R_{i-j}$)과 이에 대한 가중치($W^n_{k,R}$)를 이용해서 attention score를 계산하고 있습니다. 다만, 모든 쌍($i, j$)에 대한 positional encoding을 계산하는 것은 quadratic한 비용이 들기 때문에 실제 구현에서는 선형 계산방법을 통해 계산 절차를 간단하게 했습니다(논문의 Appendix+).

4. Experiments

4.1 Main Result

본 논문에서는 제안한 모델을 단어 단위, 문자 단위의 여러 데이터 셋으로 학습하여 기존의 SOTA모델들과 비교해보았습니다.

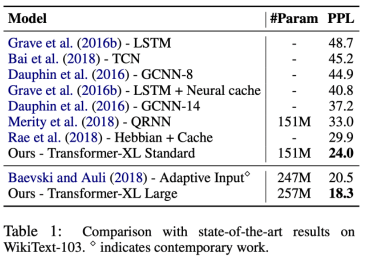
WikiText-103은 word-level의 이용가능한 가장 큰 단어 단위의 데이터셋이고, long-term dependency를 가지고 있습니다. 이전 모델보다 ppl 20.5에서 18.3까지 성능을 향상시켰습니다.

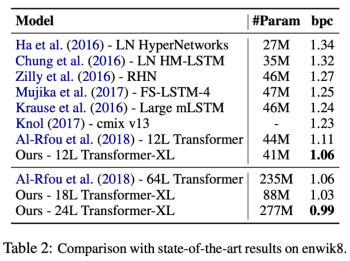
enwik8은 character-level의 전처리되지 않은 위키피디아 텍스트 데이터셋입니다. vanilla transformer와 RNN-based 모델에 비해 큰 차이로 성능이 향상되었습니다. 또한, layer수를 늘릴 수록 더 좋은 성능을 보여주고 있습니다.

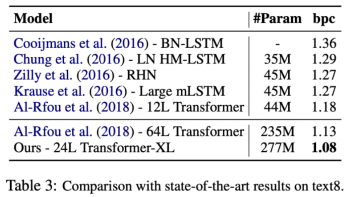
text8은 character-level의 전처리된 위키피디아 데이터입니다. a-z의 소문자만으로 구성됩니다. enwik8에서 가장 좋았던 하이퍼파라미터로 설정하여 학습을 진했했고, SOTA를 달성했습니다.

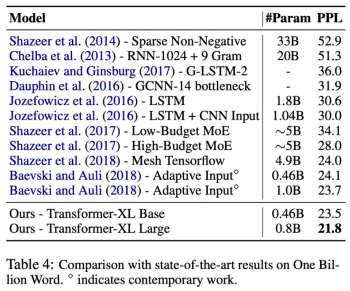
One Billion Word 데이터셋은 큰 corpus 안에 여러 문장의 순서를 섞은 데이터셋입니다. 그래서 long-term dependency를 가지지 않습니다. 주로 short-term dependency의 모델링 테스트에 사용됩니다. Transformer-XL은 long-term dependency학습에 중점을 둔 모델임에도 불구하고, 해당 데이터셋에서 SOTA를 달성하였습니다. 이를 통해 short-term dependency에도 잘 일반화한다고 볼 수 있습니다.

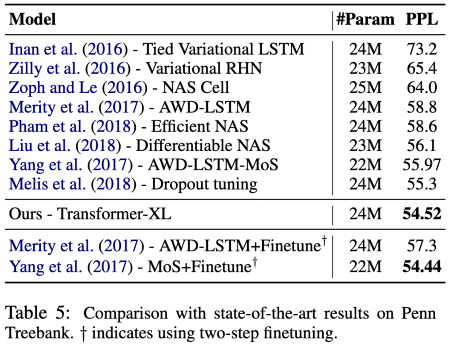
Penn Treebank 데이터셋은 단어 단위의 데이터셋입니다. Transformer-XL은 특히 해당 데이터셋에선 1M개의 토큰으로만 학습했음에도 뛰어난 성능을 보여주었는데, 작은 데이터셋에서도 잘 일반화한다고 볼 수 있습니다.

4.2 Ablation Study

Transformer-XL에서 제안된 2개의 테크닉인 recurrence mechanism과 relative positional encoding scheme의 효과를 증명합니다.

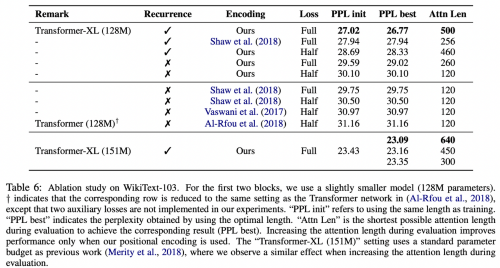
첫번째 실험은 WikiText-103을 이용했고, 해당 데이터셋은 long-term dependency를 요구하는 데이터셋이죠. 각 변수가 나타내는 의미는 다음과 같습니다.

• Recurrence
  • True: 본 논문에서 제시한 attention length만큼 Recurrence하게 연산을 진행하는 방식
  • False: Recurrence 없이 기존의 sliding window 방식
• Encoding
  • Relative Encoding: Ours, Shaw et al. (2018)
  • Absolute Encoding: Vaswani et al. (2017), Al-Rfou et al. (2018)
• Loss
  • half: 마지막에서부터 반의 위치에 있는 토큰들에 대해서만 loss를 계산하는 방식
  • full: 모든 위치에 있는 토큰들에 대해 loss를 계산하는 방식
• PPL init : 학습시 같은 길이를 사용했을 때의 PPL
• PPL best : 학습시 최적의 길이를 사용했을 때의 PPL
• Atth Len : PPL best를 얻기 위해 이용된 attention length

실험결과에서 볼 수 있듯이, 본 논문에서 제시한 Recurrence와 Relative positional encoding이 모델의 성능에 영향을 주는 것을 확인할 수 있습니다.

• 5번째 실험과 8, 9번째 실험 결과의 비교를 통해 Relative positional encoding 방식이 더 효과적인 성능을 보이는 것을 확인할 수 있습니다.
• 2번째 실험과 6번째 실험 결과의 비교를 통해 Recurrence 구조가 더 좋은 성능을 보이는 것을 볼 수 있습니다.
• 마지막 3개의 실험에서 Atten Len이 길수록 더 좋은 성능을 보이고 있습니다.

두번째 실험에서는 더 긴 문맥을 볼 수 있다는 장점이 context fragementation 문제도 해결할 수 있는지 확인해보았습니다. 확인을 위해 데이터셋은 비교적 long-term dependency를 덜 요구하는 One Billion Word를 사용해 진행하였습니다. 그리고 위 실험 결과에서 확인할 수 있듯이, long-term dependency가 중요하지 않은 작업에서도 recurrence를 이용한 경우에 더 좋은 성능을 보였습니다. 게다가 짧은 sequence에서도 Shaw et al. (2018)의 encoding방식보다 더 좋은 성능을 보여줍니다.

4.3 Relative Effective Context Length

Khandelwal et al. (2018)이 제안한 sequence 모델의 Effective Context Length(ECL)을 평가하기 위한 방법을 제안했습니다. ECL은 context길이를 늘려가면서 일정 임계점 이상 성능이 증가하는지 확인하고, 성능 향상이 일어나지 않는 순간의 context길이를 의미합니다. 하지만 ECL은 다중 모델 비교하는데 한계가 있어, 본 논문에서는 여러 모델에 공통적으로 적용해 확인할 수 있는 RECL 지표를 제안하였습니다.

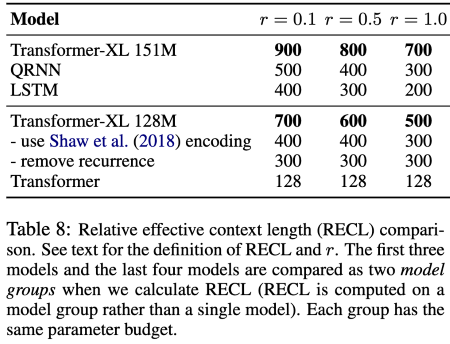
위의 표에서 보듯이 Transformer-XL이 기존의 모델들보다 최소 500개의 토큰의 정보들을 더 많이 가져갈 수 있었습니다. 이는 recurrence mechanism과 positional encoding이 RECL을 높이는데 영향을 주었음을 의미합니다.

4.4 Generated Text

중간 크기의 WikiText-103 데이터 셋으로 학습된 Transformer-XL은 수천개 가량의 토큰으로 구성된 일관된 문맥의 기사를 만들어낼 수 있었습니다.

4.5 Evaluation Speed

Vanilla Transformer 모델과 Transformer-XL과 평가 시에 속도를 비교한 실험입니다. Recurrence mechanism을 사용해 이전 세그먼트의 정보를 재사용하므로, Transformer-XL은 평가 시에 최대 1,874배 더 향상된 속도를 보여주었습니다.

5. Conclusion

Transformer-XL은 RNNs와 Transformer보다 longer-term dependency를 더 잘 모델링하였습니다. 또한, 평가 시에 상당히 더 빠른 속도로 수행하며 일관된 텍스트 기사의 생성도 가능했습니다.

하지만 대표적인 NLP 벤치마킹하는 GLUE 데이터셋을 통한 실험을 수행하지 않았고, downstream task에 대한 실험이 존재하지 않았습니다. 그래서 본 모델이 실제로 downstrem에서 backbone으로 활용될 때 실질적인 성능 향상이 일어났는지는 보여주지 못한 것이 아쉽습니다.