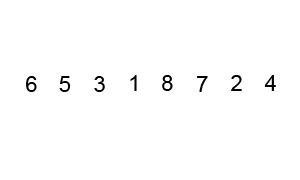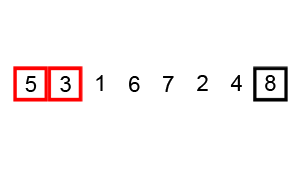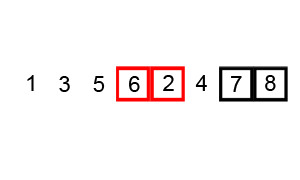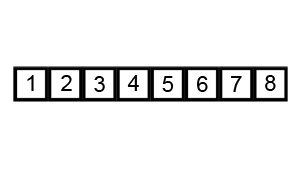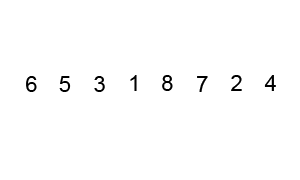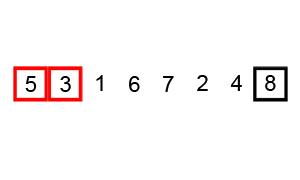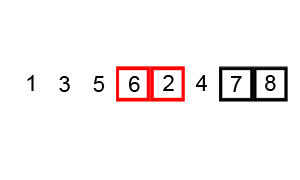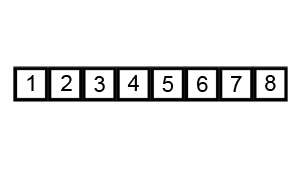버블 정렬
버블 정렬의 컨셉은 **앞,뒤를 비교해서 큰 값을 뒤로 보내줌~!! 이다.
즉 [a1,a2,a3,a4]가 있다고 하면 a1,a2를 비교하고 더 큰 수를 a3과 비교하고 그 중 더 큰 수를 a4와 비교하면 된다.
만약에 a1,a2,a3,a4가 각각 [1,4,3,2]이라고 가정하고 진행해보자
a1,a2(1,4)를 비교하면 a2가 더 크다 그러므로 a3과 비교할 대상은 a2가 된다.
[a1,a2,a3,a4] = [1,4,3,2]
따라서 a2,a3(4,2)가 비교 되는데 둘중 더 큰 수는 a2임으로 다음 대상인 a4와 비교할 값은 더 큰 수인 a2가 된다.
[a1,a3,a2,a4] = [1,3,4,2]
마지막으로 비교를 하게 되면 a2,a4(4,3) 더 큰 수는 a2임으로 a2가 뒤로 가게 된다.
[a1,a3,a4,a2] = [1,3,2,4]
이렇게 버블 정렬이 끝나게 된다. 그 결과 가장 마지막에 있는 값인 a2가 가장 큰 값인 4라는 것을 알게 되었다.
하지만!
가장 큰값이 끝으로 갔지만 나머지 a1,a3,a4는 정렬이 되어 있지 않은 상태이다. 이를 정렬해주기 위해서는 앞의 과정을 반복해주면 된다. 즉 앞의 과정이 데이터 값중 가장 큰 값을 뒤로 보내주는 과정이라고 하면
위으 작업을 한번더 반복한다면 a1,a3,a4의 값 중에서 가장 큰 수가 뒤로 가게 될 것이다. 그러면 [X,X,2번째로 큰 값, 가장 큰 값]이 나올것이다. 이 과정을 끝까지 반복하면
[4번째로 큰 값, 3번째로 큰 값, 2번쨰로 큰 값, 가장 큰 값]으로 정리가 될 것이다.
이를 코드로 작성하게 되면 다음과 같다.
def buble(data):
for index in range(len(data)-1):
for index2 in range(len(data)-index-1):
if data[index2] > data[index2+1]:
data[index2], data[index2+1] = data[index2+1], data[index2]
return data 하지만 알고리즘을 사용하는 이유는 메모리를 더 효율적으로 사용하기 위해서이다. 위의 코드로 충분히 정렬이 끝이 나지만 만약에 처음부터 데이터가 정렬 된 상태로 들어오더라도 4개의 데이터 비교 기준 6번의 불필요한 비교가 실행된다.
따라서 좀더 효율적인 정렬을 하기 위해서는 남은 데이터가 정렬인지를 먼저 파악을하고 정렬이 아닌 상태라면 비교를 진행한다 라는 코드가 추가가 된다면 더 효율적인 코드를 작성 할 수 있다.
def buble(data):
for index in range(len(data)-1):
sort = False #정렬 상태 초기화
for index2 in range(len(data)-index-1):
if data[index2] > data[index2+1]:
data[index2], data[index2+1] = data[index2+1], data[index2]
sort = True #한번이라도 swap이 발생하면 True
if sort == False: #만약 정렬이 된 상태라면 더이상의 반복을 하지 않음
break
return data