이진 트리와 이진 탐색 트리
이진 트리
노드의 최대 브랜치가 2인 트리
이진 탐색 트리
이진 트리에서 (왼쪽 자식 노드는 부모 노드보다 작은 값, 오른쪽 자식 노드는 큰 값을 가지고 있는)다음과 같은 조건이 추가된 트리

그럼 이진 탐색 트리는 언제 사용을 하는가?
이진 탐색 트리는 보통 원하느 데이터를 찾을 때 많이 사용한다.
데이터를 찾을 때 사용하는 좋은 자료구조는 데이터를 찾는 속도가 빠른 자료구조이다.
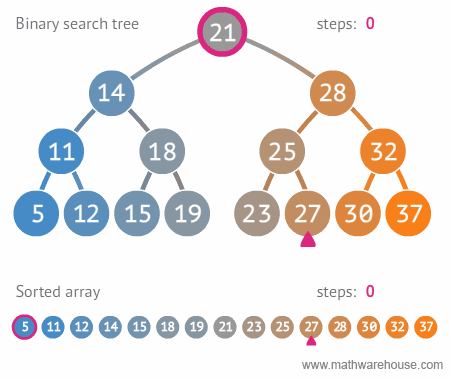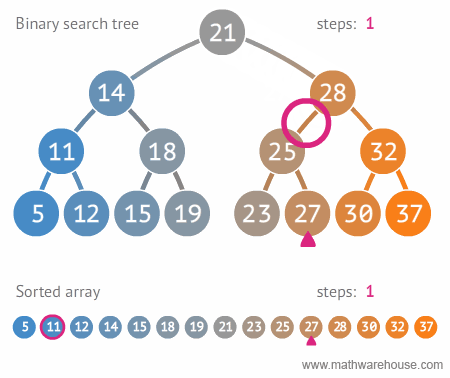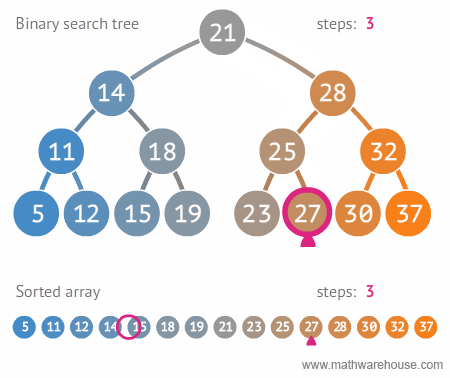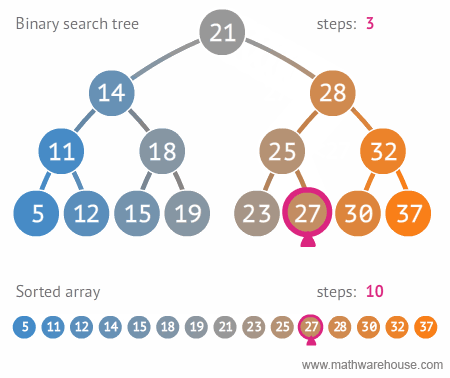
이진 트리 탐색 자료구조와 배열 자료구조를 비교해보면 확실히 이진 탐색 트리가 더 빠르다는 것을 알수 있다.
이진탐색트리 특징
- 모든 노드는 유일한 키를 갖는다.
- 왼쪽 서브트리의 키들은 루트의 키보다 작다
- 오른쪽 서브트리의 키들은 루트의 키보다 크다.
- 왼쪽과 오른쪽 서브트리도 이진탐색트리이다.
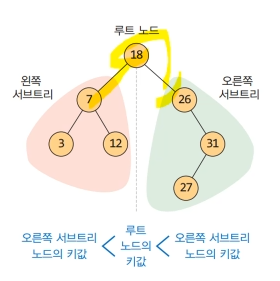
이진탐색트리의 연산
(순환)
def search_bst(n,key):
if n == None: // key가 트리에 없는 경우
return None
elif key == n.key // key와 노드의 값이 일치하는경우
return n
elif key < n.key: // key가 노드의 값보다 작은 경우 왼쪽 서브트리 넣어서 실행
return search_bst(n.left,key)
else: //key가 노드의 값보다 큰 경우 오른쪽 서브트리 넣어서 실행
return search_bst(n.right,key)
(반복)
def search_bst_iter(n,key):
while n != None: //key가 트리에 없지 않는 동안 반복
if key == n.key: // key와 노드의 값이 일치하는경우
return n
elif key < n.key: // key가 노드의 값보다 작은 경우 왼쪽 서브트리 넣어서 실행
n= n.left
else:
n=n.right //key가 노드의 값보다 큰 경우 오른쪽 서브트리 넣어서 실행
return None // key가 트리에 없음(최대 노드와 최소 노드 찾기)
def find_max(n):
while n != None and n.rhgit != None: // 노드 n이 존재하고 오른쪽 서브트리가 존재하는 동안 반복
n=n.right // 오른쪽 노드를 기준 노드로 설정하고 다시 탐색
return n // 가장 오른쪽의 노드(최대값) 출력
def find_min(n):
while n != None and n.left != None: // 노드 n이 존재하고 왼쪽 서브트리가 존재하는 동안 반복
n=n.left // 왼쪽 노드를 기준 노드로 설정하고 다시 탐색
return n // 가장 왼쪽의 노드(최소값) 출력
(삽입) 기본적인 이진탐색트리의 조건을 유지하면서
삽입 연산은 탐색에 실패한 위치에 노드를 삽입하는 것
def insert_node(new,tree):
if new.key < tree.key: // 새로운 노드의 값이 기존 노드의 값보다 작으면
if tree.left is None: // 기존 노드의 왼쪽 자식이 없으면
tree.left = new // 왼쪽 노드의 값에 새로운 노드 값 삽입
return True
else : // 기존 노드의 왼쪽 자식이 있다면
return insert_node(new,tree.left) // 기존 노드의 왼쪽 자식의 값과 새로운 값 비교
elif new.key > tree.key: // 새로운 값이 기존 노드의 값보다 크다면
if tree.right is None: // 기존 노드의 오른쪽 자식이 없으면
tree.right = new // 기존 노드의 오른쪽 값에 새로운 노드 값 삽입
return True
else : // 기존 노드의 오른쪽 자식이 있다면
return insert_node(new, tree.right) // 기존 노드의 오른쪽 자식의 값과 새로운 값 비교
else :
return False(삭제) 기본적인 이진탐색트리의 조건을 유지하면서
case 1: 단말 노드 삭제
def delete_case1(parent, node, root):
if parent is None: # 부모가 없다면
root = None # root는 공백 트리이다.
else :
if parent.left == node : #왼쪽 자식의 노드가 삭제할 노드라면
parent.left = None # 왼쪽 자식의 노드를 None으로 지워준다.
else : #오른쪽 자식의 노드가 삭제할 노드라면
parent.right = None #오른쪽 자식의 노드를 None으로 지워준다.
return rootcase 2: 자식이 하나인 노드의 삭제
def delete_case2(parent, node, root): #자식이 하나인 노드의 삭제
if node.left is not None: # 노드의 자식이 왼쪽일 때
child = node.left # child에 왼쪽 자식의 값 넣기
else : # 노드의 자식이 오른쪽일 때
child = node.right #child에 오른쪽 자식의 값 넣기
if node == root : # 삭제하려는 노드가 루트일 경우
root = child #루트 노드에 child 값 넣기
else: #삭제하려는 노드가 루트 노드가 아닌경우
if node is parent.left: #삭제 하려는 노드가 부모의 왼쪽 자식이면
parent.left = child #삭제한 자리에 child 값 넣기
else: #삭제 하려는 노드가 부모의 오른쪽 자식이라면
parent.right = child #삭제한 자리에 child 값 넣기
return rootcase 3: 자식이 두개인 노드의 삭제
가장 비슷한 값을 가진 노드를 석제 위치로 가져온다.
여기서 가장 비슷한 값은 삭제하고자 하는 노드의 왼쪽 서브트리의 가장 큰 노드 값이나, 삭제하고자 하는 노드의 오른쪽 서브트리의 가장 작은 노드 값을 선택하는 것
이 노드의 값들이 삭제하려는 노드의 값과 가장 유사하기 때문이다.
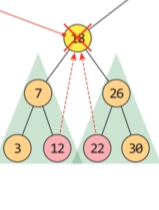
아직 이해가 잘 안됨
def delete_case3(parent,node,root):
succp = node #후계자의 부모 노드
succ = node.right #후계자 노드 (임의로 오른쪽의 값을 선택함)
while (succ.left != None) : # 오른쪽을 선택했으니 가장 작은 값을 찾는 과정
succp = succ
succ = succ.left
if (succp.left == succ) :
succp.left = uscc.right
else:
succp.right=succ.right
node.key = succ.key
node.value=succ.value
node=succ;
return root삭제 연잔의 전체 코드
def delete_all_case(root,key):
if root == None : return None #공백 트리인 경우 공백으로 반환
parent = None #삭제할 노드의 부모 변수 선언
node = root #삭제할 노드 탐색
while node != None and node.key != key: #전체노드에서 삭제할 노드를 찾는 과정
parent = node
if key < node.key : node = node.left
else : node = node.right;
# 삭제하려는 노드를 찾음 거나 삭제할 노드가 존재하지 않음
if node == None: return None # 삭제할 노드가 존재하지 않음
if node.left == None and node.right == None: #삭제하려고 하는 노드가 단말 노드인 경우
root = delete_case1(parent,node,root)
elif node.left == None or node.right == None: # 삭제하려고 하는 노드의 자삭이 하나 인경우
root = delete_case2(parent,node,root)
else: # 삭제하려고 하는 노드가 2개인 경우
root = delete_case3(parent,node,root)
return root