[논문] Deep Residual Learning for Image Recognition (2015)

메르센고수·2024년 2월 26일
Computer VisionDeep LearningResnetpython논문 요약

Review

목록 보기
1/5
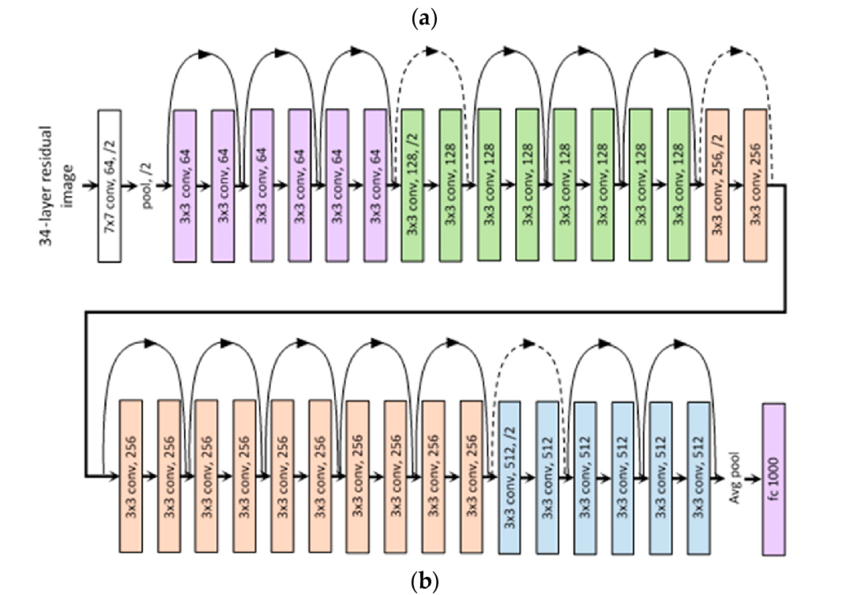
post-thumbnail

처음으로 논문 요약을 해보고 블로그에 쓰는 글이라 서투른 점 이해부탁드립니다

졸업 프로젝트를 시작하면서 주제에 맞게 딥러닝 알고리즘에 대해 익숙해지고 효율적인 딥러닝 알고리즘을 찾아서 구현해보고자 팀원들끼리 각자 관심있는 주제와 관련 있는 딥러닝 관련 논문을 찾아서 읽고 발표해보는 시간을 갖기로 하였고,
나는 컴퓨터비전 쪽으로 진로를 설정하였기에 이미지 처리에 있어서 중요한 논문이기도 하고 2015년에 나왔음에도 여전히 실무에 쓰일 정도로 중요한 이론인 ResNet에 대해 요약하고 발표하기로 하였다.
따라서 이 글을 통해 ResNet이 무엇인지, 어떻게 이런 알고리즘을 생각하게 되었고 구현은 어떻게 하는지 전반적인 내용에 대해서 살펴보겠습니다.

참고

ResNet 논문 출처
CNN (Convolutional Neural Network) - WIKIPEDIA
Review : ResNet - winner of ILSVRC 2015

Introduction

컴퓨터 비전 분야에서 CNN(Convolutional Neural Network)는 여전히 중요한 위치에 존재하고 있다. 최근에 Transformer라는 혁명적인 모델이 등장하면서 컴퓨터 비전에서도 Transformer 모델을 적용한 알고리즘이 많이 사용되기는 하지만 여전히 CNN은 중요한 개념이고 자주 쓰인다.
ResNet을 들어가기 전, VGGNet이라는 모델이 등장했었는데 VGGNet이 등장하면서 이미지 분류를 위해 점점 더 깊은 모델이 생성되고 feature representation의 성능이 모델의 깊이와 비례한다는 것이 증명되어 갈수록 깊이가 더 깊어지는 모델들이 생성되었다. 그러나, 모델이 너무 깊어지게 되어 일정 깊이 이상이 될 경우 오히려 얕은 깊이일 때보다 성능이 안좋아지는 문제가 발생했는데 이를 degradation problem이라고 한다.

그렇기 때문에 연구원들은

"Is learning better networks as easy as stacking more layers?"

질문을 던지면서 degradation problem에 대한 해결책을 고민했고 이를 overfitting과 연관지어 이해해보려고 하였다. 그러나, Overfitting의 경우 training data의 성능은 높지만 test data는 성능이 안좋다는 문제인 반면 degradation problem은 training과 test 모두 성능이 좋지 못하기 때문에 overfitting과 관련이 없다고 여기게 되었고 이러한 점 때문에 더욱 더 이목을 끌게 되었다.

따라서 연구자들은 이 과정을 통해 다음과 같은 결론을 내렸다.

  • 모델의 깊이가 깊어지면서 성능이 안좋아지는 원인은 overfitting이 아니라, 최적화(optimization)가 힘들어서 생긴 문제이다.
  • Exploding / Vanishing gradient 문제가 모델 깊이가 깊어질 수록 발생할 확률이 높아지기 때문이다.


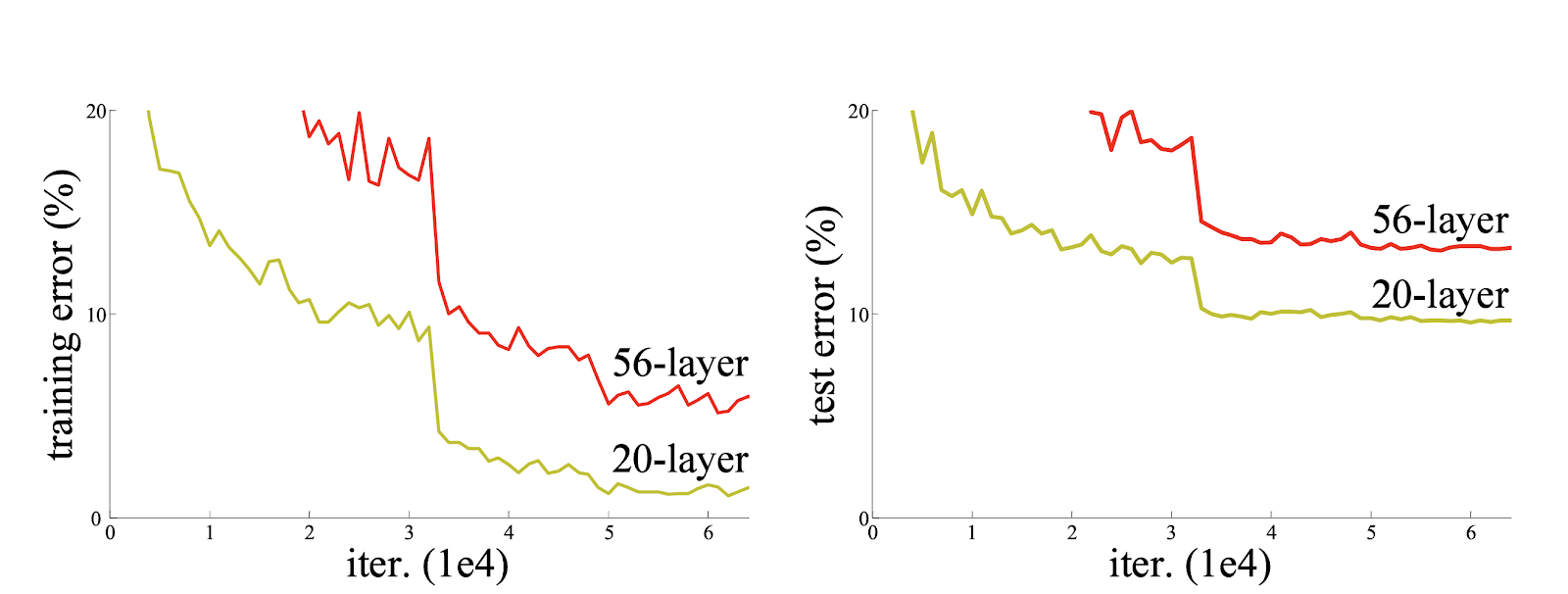
이렇게 깊이가 깊어질수록 최적화가 어려워진다는 문제를 알았기 때문에 이에 대한 해결책으로 깊은 모델을 만드는데, 이 과정에 추가되는 layer는 identity mapping으로 추가를 하고 나머지는 얕은 모델에서 훈련시킨 layer를 복사해오는 방식으로 구현을 했지만 이 역시 좋은 해결책은 되지 못하였다.
여기서 등장한 개념이 Deep Residual learning framework이다.
간단히 이 framework에 대해 설명을 하자면, 쌓여진 layer가 바로 그 다음 layer에 적재되는 것이 아니라 Residual mapping에 적합하도록 만드는 것이다.

Instead of hoping each few stacked layers directly fit a desired underlying mapping, we explicitly let these layers fit a residual mapping.


H(x)=F(x)+xH(x) = F(x) + x로 두어 Residual mapping이 최적화에 적합하다고 가정을 하였다. 왜냐하면 H(x)H(x)를 미분하게 되면 H′(x)=F′(x)+1H'(x) = F'(x) + 1이 되는데, 무조건 1을 더해주기 때문에 gradient 값이 0에 수렴하게 되어 생기는 Vanishing gradient 문제를 방지할 수 있기 때문이다.
여기서 F(x)+xF(x) + x를 Shorcut Connection이라고 한다. 여기서는 Identity mapping을 통해 하나 이상의 layer를 skip할 수 있게 해주는데 추가적인 parameter도 필요없고 계산이 복잡해지지 않는다는 점이 장점이다.

결과적으로 이 논문에서 저자가 해결하고자 하는 목표는 크게 두 가지라고 말할 수 있다.

  1. Plain Net보다 ResNet에서의 최적화가 더 쉽다는 것을 보이기
  2. Network의 깊이가 깊어져도 ResNet에서는 degradation problem 없이 성능이 좋아진다는 것을 보이는 것

여기 까지가 Introduction이고 이제 본론으로 넘어가 ResNet에 대해 자세히 다뤄보고자 한다.

Deep Residual Learning

쉽게 생각해서 Deep Learning + Residual Learning 이 둘을 합친 개념이다. 네트워크의 깊이를 점점 더 깊게 만들면서 Residual Learning을 적용해서 일정 깊이 이상의 Layer가 적재되어 있어도 최적화를 통해 성능이 안좋아지는 것을 방지할 수 있다는 것을 보이는 것이 이 논문이 말하고자 하는 바이다.

Residual Learning

Residual이라는 단어를 사전에 찾아보면,

잔여의, 잔류의, 나머지의 이러한 의미가 많다. 하지만 수학적인 의미로는 ∣y^−y∣|\hat{y}-y|라는 의미가 존재한다. 즉, 예측값-실제값의 크기를 의미한다. 어떻게 보면 당연한 의미인데, 아까 설정한 H(x)=F(x)+xH(x) = F(x) + x를 F(x)F(x)에 대해 정리하면 F(x)=H(x)−xF(x) = H(x) - x가 되는데, 이것이 곧 예측값-실제값의 형태이기 때문이다.

Identity Mapping by Shortcuts


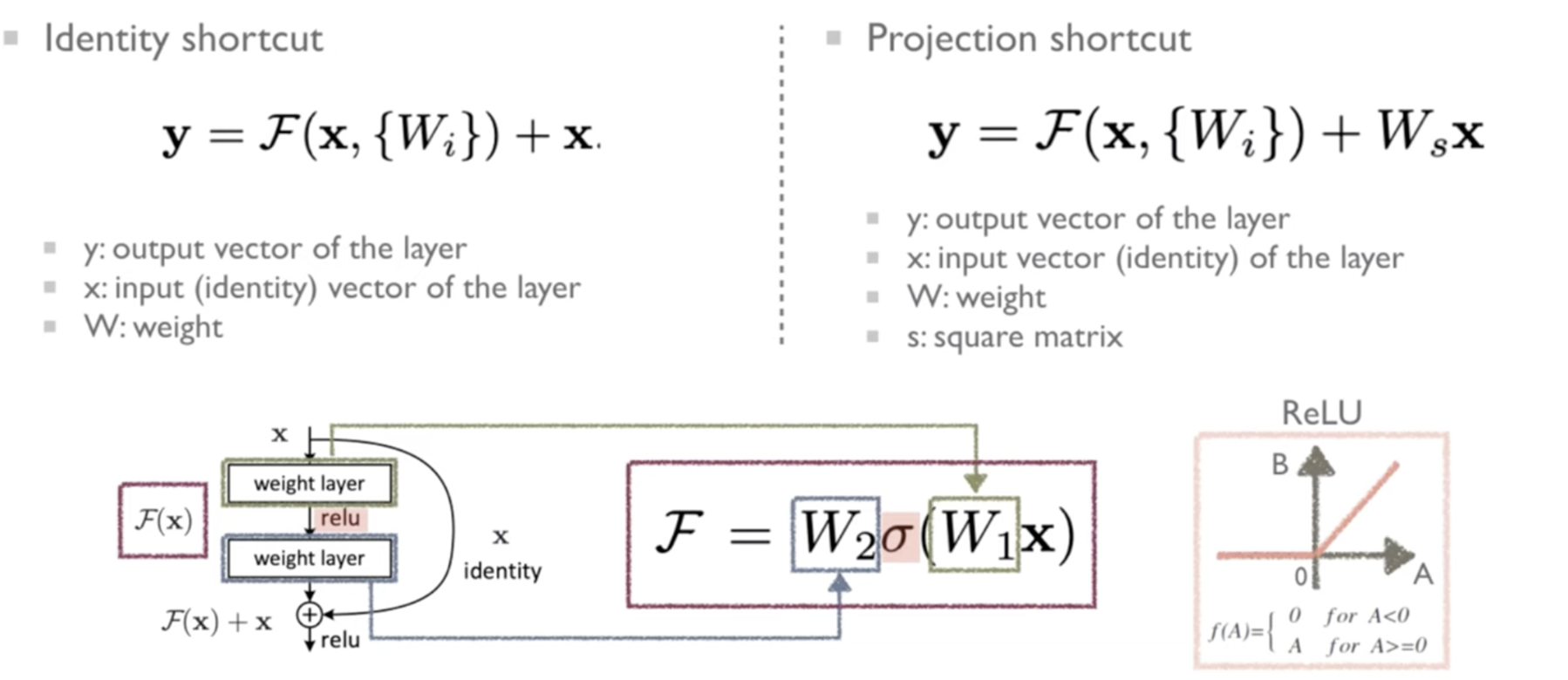
왼쪽의 Identity shortcut의 경우 밑에 있는 F=W2σ(W1x)F=W_2\sigma(W_1x)를 간소화한 모양이다. 여기서 오른쪽 Projection shortcut으로 넘어가게 되면, 뒤에 붙은 Identity mapping 항에 WsW_s가 붙은데, 이는 단순히 FF와 xx의 차원을 동일하게 맞춰서 덧셈 연산을 수행할 수 있도록 하기 위함이다.

Network Architecture


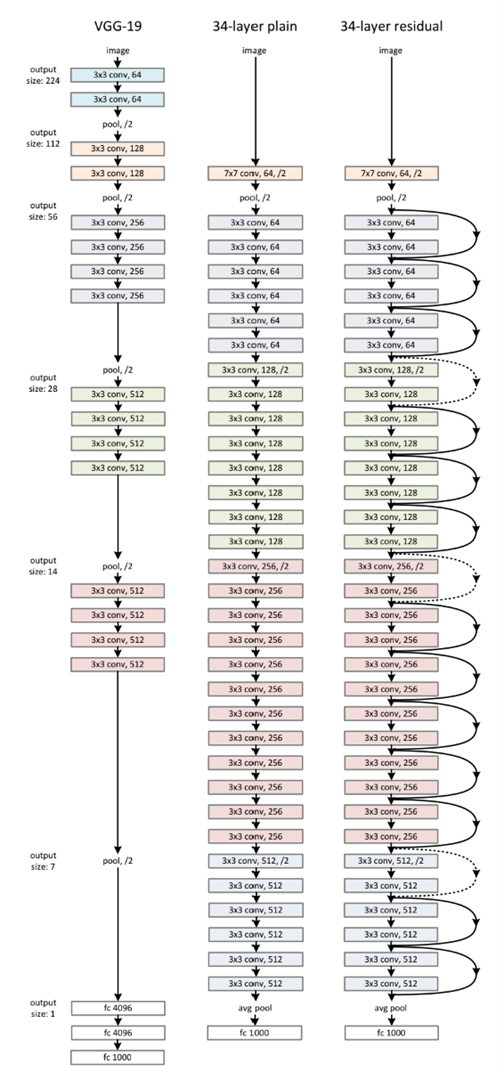
왼쪽부터 VGGNet, Plain Net, Residual Net이다.'

이 중 Plain Net과 Residual Net을 비교한 것을 표로 나타내면 다음과 같다.

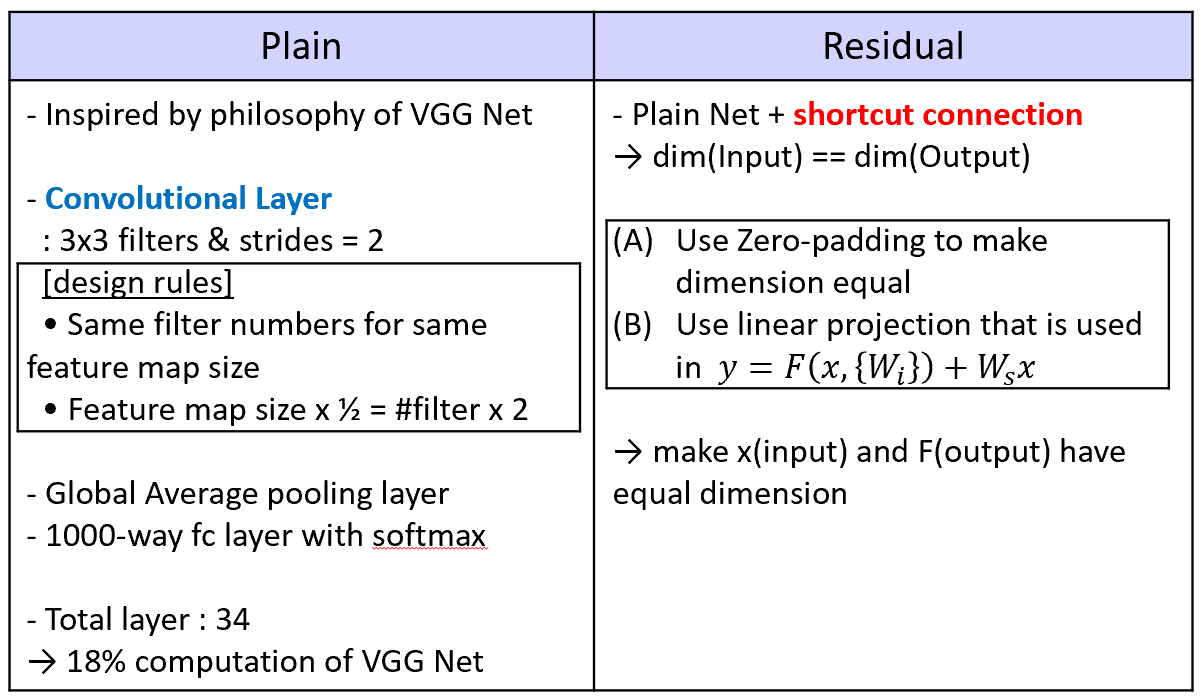
Plain Net

  1. VGG Network의 영향을 받았다.
  2. Convolution Layer
    • 3x3 filter와 stride 2
    • 같은 크기의 map에 대해서는 같은 filter 개수를 갖는다
    • feature map의 size가 절반이 되면 filter의 개수는 2배가 된다.
  3. Global Average pooling layer 사용
  4. 마지막에 softmax로 1000-way fully connected layer를 통과시킨다.
  • VGG Net보다 적은 filter의 개수와 복잡도를 갖고 연산의 18%밖에 하지 않는다.

Residual Net

  1. Plain Net에 shortcut connection을 적용한 개념이다.
  2. 차원을 동일하게 맞춰주기 위해 2가지 방법 사용
    • zero-padding
    • linear-projection (아까 xx앞에 곱해준 WsW_s)

Implementation

이 논문에서 구현한 방식도 표로 정리하면 다음과 같다.

그리고 실제로 이를 토대로 pytorch로 구현을 해보았다.
구현 내용에 대해서는 아래쪽에서 자세히 다루고 내 github 주소를 첨부할 것이다.

Experiment

1. ImageNet Classification




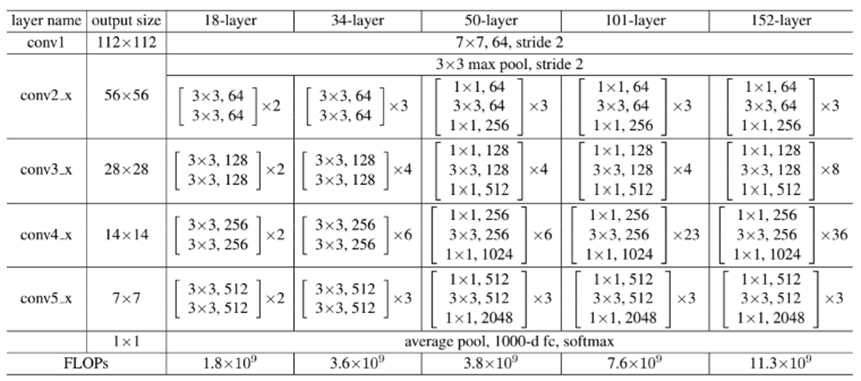
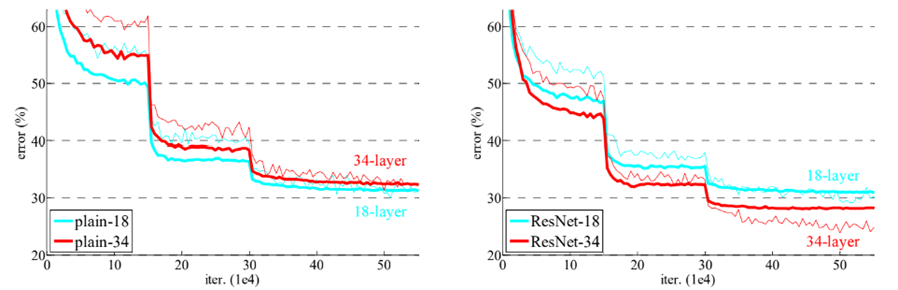
위의 표와 그래프를 보면, 18 Layer일 때는 plain net과 ResNet의 성능차이가 거의 없지만 34개로 늘리게 될 경우 확연히 차이가 커진 것을 확인할 수 있다. 이를 통해 기존에 존재했던 depth가 늘어나면서 생긴 degradation problem이 residual net을 통해 효과적으로 처리된 것을 확인할 수 있다.

This indicates that the degradation problem is well addressed in this setting and we manage to obtain accuracy gains from increased depth.

또한 그래프 오른쪽의 ResNet의 수렴속도도 더 빠르다는 것을 확인할 수 있다.

두 번째로 top-1 err와 top-5 err를 기준으로 여러개의 모델들을 비교하였다.
먼저, VGGNet과 GoogLeNet, PReLU_net을 비교하고 그 다음에는 plain과 ResNet을 A,B,C기준으로 나누어서 마지막으로는 ResNet의 Layer depth에 따라 성능 비교를 하였다.
이 논문에서는 A,B,C로 나눈것과 depth를 기준으로 나눈 것 위주로 다루었다.
(논문의 주된 목적이 degradation problem을 해결하는 것이기 때문)

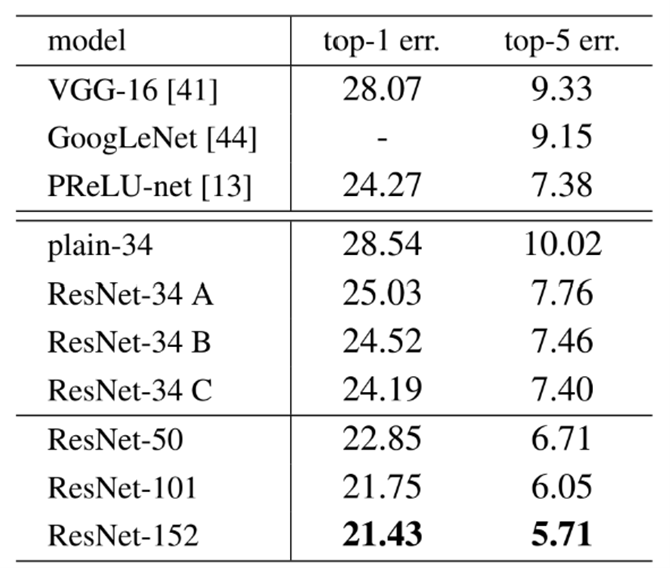
Identity vs Projection shortcuts

(A)zero-padding shortcuts
(B)projection-shortcuts (for increasing dimensions), 나머지는 identity
(C)모든 shortcut이 projection

위의 표를 보면, Plain Net<A<B<C 순으로 성능이 좋아진다는 것을 확인할 수 있다. 그러나 이것들은 degradation problem을 다루는데 필수적인 것이 아니라는 것을 나타낸다. (difference가 매우 작기 때문에)

But the small differences among A/B/C indicate that projection shortcuts are not essential for addressing the degradation problem

Deeper Bottleneck Architecture

Training time의 개선을 위해 bottleneck design으로 model의 구조를 변경하였다. 1x1 - 3x3 - 1x1 구조로 3개의 layer를 쌓는 방식을 이용하였다. Bottleneck design을 사용한 이유는 기존의 구조와 비슷한 복잡성을 가지면서 input과 output의 차원을 줄일 수 있기 때문이다.

예를 들어, 아래의 그림을 기준으로 parameter의 개수를 확인해보면

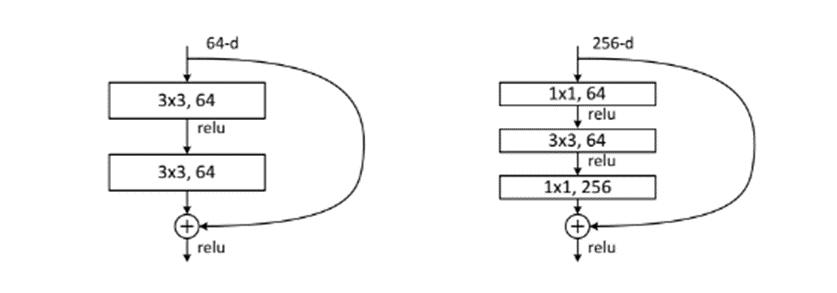
기존 모델의 경우 2∗(3∗3∗64)=11522*(3*3*64)=1152개의 parameter이지만, Bottleneck을 적용한 모델의 경우 1∗1∗64+3∗3∗64+1∗1∗256=8961*1*64+3*3*64+1*1*256=896으로 Layer의 개수가 늘어났음에도 불구하고 parameter의 개수는 오히려 줄어든 것을 확인할 수 있다.

또한 아까 표에서의 50/101/152 Layer를 비교하면 34-Layer일 때보다 정확도가 더 향상된 것을 확인할 수 있다. 이를 SOTA(State-of-the art) method와 비교해보기 위해 위에서 언급한 6가지의 모델을 앙상블 기법으로 적용해본 결과 error를 3.57%까지 줄일 수 있었고 이 모델이 ILSVRC 2015에서 우승을 한 모델이라고 한다.

2. CIFAR-10 and Analysis




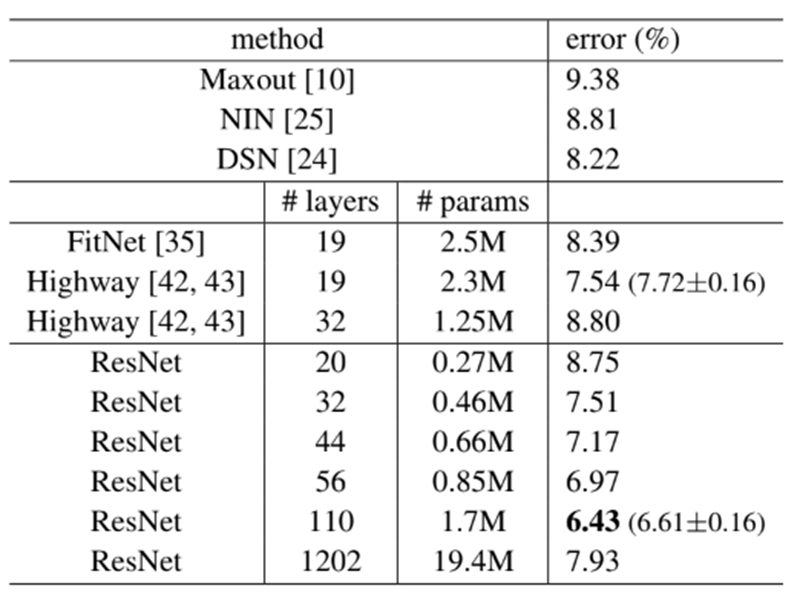
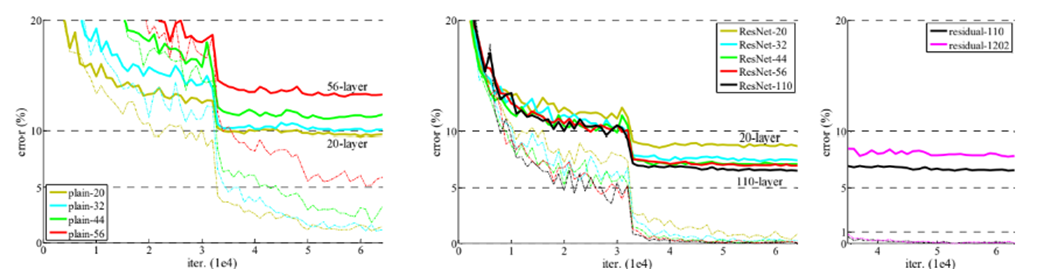
위의 표와 그래프를 해석해보면 이 논문에서 밝히고 싶던 layer의 깊이와 성능 사이의 관계가 이젠 layer가 깊어져도 성능도 높아진다는 것을 확인할 수 있다. 즉, degradation problem이 발생하지 않는다는 것을 알 수 있다. 그러나, Layer의 개수가 1000개가 넘어가게 되면 갑작스럽게 성능이 안좋아지게 되는데 이는 overfitting으로 인한 문제이다.
따라서 maxout이나 dropout 같은 strong regularization 기법들을 적용해서 최적의 결과를 얻을 수 있도록 해야한다.

3. Object Detection on PASCAL and MS COCO


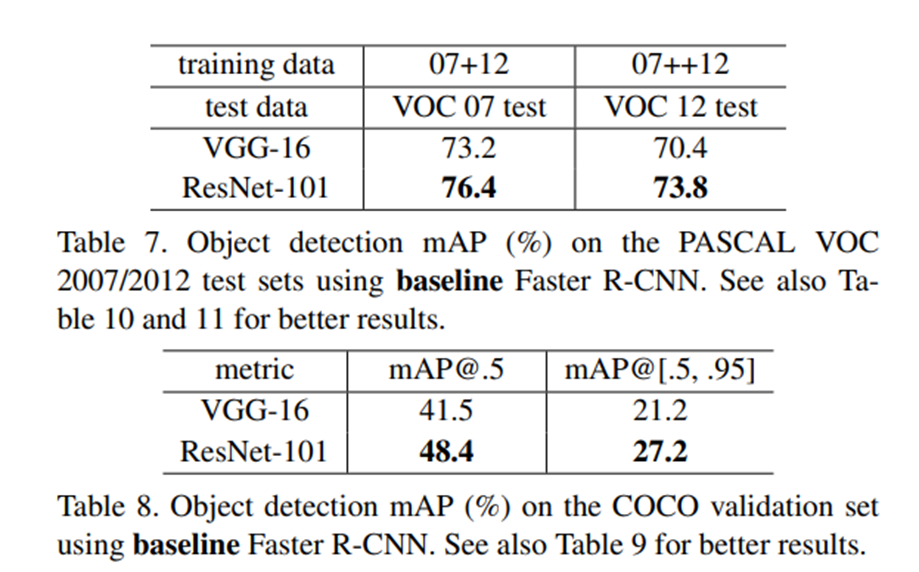
이 part에서도 성능이 좋아졌다는 주장이 주를 이룬다. 다만, 특이한 점이 있다면 detection method로 Faster R-CNN을 적용했다는 것이다.
Faster R-CNN에 대한 설명은 논문 링크를 걸어두겠다.

Faster R-CNN 논문

Pytorch 구현

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torchvision import datasets, transforms
from torch.utils.data import random_split

transform = transforms.Compose([
    transforms.ToTensor(),
    transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))
])

# CIFAR10 dataset 불러오기
dataset = datasets.CIFAR10(root='./data', train=True, download=True, transform=transform)

# 80%는 train-set, 나머지 20%는 test-set으로 분리
train_size = int(0.8 * len(dataset))
val_size = len(dataset) - train_size
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])

partition = {'train': train_dataset, 'val': val_dataset}



def conv3x3(in_planes, out_planes, stride=1):
    return nn.Conv2d(in_planes, out_planes, kernel_size=3, stride=stride, padding=1, bias=False)

class BasicBlock(nn.Module):
    def __init__(self, in_planes, out_planes, stride=1):
        super(BasicBlock, self).__init__()
        self.conv1 = conv3x3(in_planes, out_planes, stride)
        self.bn1 = nn.BatchNorm2d(out_planes)
        self.conv2 = conv3x3(out_planes, out_planes)
        self.bn2 = nn.BatchNorm2d(out_planes)

        self.shortcut = nn.Sequential()
        if stride != 1 or in_planes != out_planes:
            self.shortcut = nn.Sequential(
                nn.Conv2d(in_planes, out_planes, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(out_planes)
            )

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.bn2(self.conv2(out))
        out += self.shortcut(x)
        out = F.relu(out)
        return out

class ResNet(nn.Module):
    def __init__(self, block, num_blocks, num_classes=10):
        super(ResNet, self).__init__()
        self.in_planes = 64

        self.conv1 = conv3x3(3,64)
        self.bn1 = nn.BatchNorm2d(64)
        self.layer1 = self._make_layer(block, 64, num_blocks[0], stride=1)
        self.layer2 = self._make_layer(block, 128, num_blocks[1], stride=2)
        self.layer3 = self._make_layer(block, 256, num_blocks[2], stride=2)
        self.layer4 = self._make_layer(block, 512, num_blocks[3], stride=2)
        self.linear = nn.Linear(512, num_classes)

    def _make_layer(self, block, planes, num_blocks, stride):
        strides = [stride] + [1]*(num_blocks-1)
        layers = []
        for stride in strides:
            layers.append(block(self.in_planes, planes, stride))
            self.in_planes = planes
        return nn.Sequential(*layers)

    def forward(self, x):
        out = F.relu(self.bn1(self.conv1(x)))
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = F.avg_pool2d(out, 4)
        out = out.view(out.size(0), -1)
        out = self.linear(out)
        return out

def ResNet18():
    return ResNet(BasicBlock, [2,2,2,2])


def train(model, dataset, optimizer, criterion, batch_size):
    dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)
    model.train()
    running_loss = 0.0
    correct = 0
    total = 0

    for data in dataloader:
        inputs, labels = data
        inputs = inputs.cuda()
        labels = labels.cuda()

        optimizer.zero_grad()

        outputs = model(inputs)
        loss = criterion(outputs, labels)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        _, predicted = outputs.max(1)
        total += labels.size(0)
        correct += predicted.eq(labels).sum().item()

    train_loss = running_loss / len(dataloader)
    train_acc = 100 * correct / total

    return train_loss, train_acc

여기까지가 기본적인 모델과 train 함수까지의 구현이고, 이 다음부터는 training과 matplotlib으로 시각화한 부분이다.

import matplotlib.pyplot as plt

num_epochs = 10
learning_rate = 0.001
train_batch_size = 64

model = ResNet18()
model = model.cuda()
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.CrossEntropyLoss()

train_loss_list = []
train_accuracy_list = []

for epoch in range(num_epochs):
    train_loss, train_acc = train(model, partition['train'], optimizer, criterion, train_batch_size)

    train_loss_list.append(train_loss)
    train_accuracy_list.append(train_acc)

    print(f"Epoch {epoch + 1}/{num_epochs}, Train Loss: {train_loss:.4f}, Train Acc: {train_acc:.2f}%")

plt.figure(figsize=(12, 4))
plt.subplot(1, 2, 1)
plt.plot(train_loss_list, label='Train Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Train Loss during Training')
plt.legend()

plt.subplot(1, 2, 2)
plt.plot(train_accuracy_list, label='Train Accuracy')
plt.xlabel('Epochs')
plt.ylabel('Accuracy')
plt.title('Train Accuracy during Training')
plt.legend()

plt.tight_layout()
plt.show()
Epoch 1/10, Train Loss: 1.3489, Train Acc: 50.76%
Epoch 2/10, Train Loss: 0.8688, Train Acc: 69.28%
Epoch 3/10, Train Loss: 0.6506, Train Acc: 77.19%
Epoch 4/10, Train Loss: 0.5114, Train Acc: 82.15%
Epoch 5/10, Train Loss: 0.3995, Train Acc: 86.09%
Epoch 6/10, Train Loss: 0.3091, Train Acc: 89.25%
Epoch 7/10, Train Loss: 0.2337, Train Acc: 91.65%
Epoch 8/10, Train Loss: 0.1698, Train Acc: 94.02%
Epoch 9/10, Train Loss: 0.1192, Train Acc: 95.78%
Epoch 10/10, Train Loss: 0.0972, Train Acc: 96.62%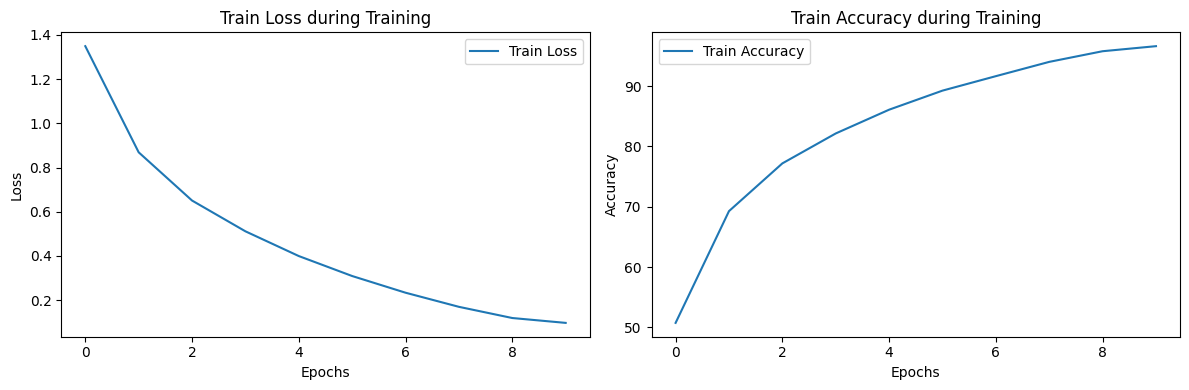


train을 할 수록 loss가 줄어들고 그만큼 accuracy가 증가하여 100%에 수렴해간다는 것을 확인할 수 있다.

profile
메르센고수
블로그 이전했습니다 (https://phj6724.tistory.com/)
다음 포스트

[논문] Attention Is All You Need

0개의 댓글