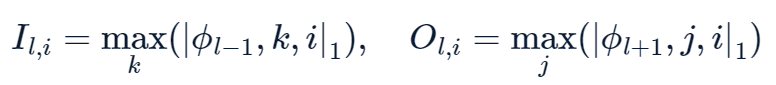KAN: Kolmogorov–Arnold Networks

1. Background

최근 연구 동향

MLP

• 딥러닝 모델의 기본이 되는 알고리즘이자, 구성 요소
• 비선형 함수를 근사하는 목적으로 사용되며, Universal Approximation Theory에 의해 표현력이 보장됨

Transformer

• 최근에 거의 모든 모델에 사용되고 있으며, FFN으로 MLP를 사용함

MLP의 한계

• 비선형 함수를 근사하지만, 해석력이 부족
• Transformer 에서 학습 파라미터는 대부분 MLP이기에, 너무 많은 파라미터를 요구함
• 고차원 함수를 근사할 때, 차원의 저주 문제가 발생할 수 있음

KAN 구조 제안

• (연산량 측면) 다변수 연속 함수를 단일 변수 함수들의 합으로 근사할 수 있음
• (해석력 측면) 노드 대신 엣지(Weight)에 학습 가능한 활성함수를 사용
• (효율성 측면) 각 Weight는 MLP에서는 Linear(선형 가중치)를 사용하였으나, 이것을 단변량 함수로 대체하며, 스플라인으로 학습 가능하게 만듬
• (차원의 저주) 단변량 함수로 대체한다는 것은, 고차원 문제를 저차원의 여러 문제들로 해결한다는 것임.

2. Method

Motivation

• Kolmogorov-Arnold 정리에 의해, 다변수 연속 함수 f(x)를 단일 변수 연속함수들과 덧셈의 유한한 조합으로 분해할 수 있음
  
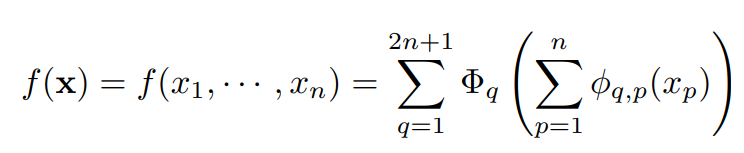
• f(x) : n개의 입력변수를 가진 입력 벡터를 다변수 연속 함수에 통과
• Φ : 단일변수 함수

예제

입력변수가 2차원의 데이터(n=2) 라고 할 때, f(x1,x2) 는 5개(2n+1)의 Φ(단일변수 함수)의 합으로 표현되며, 각 Φ(단일변수 함수)는 두개의 단일변수 함수의 합을 인수로 가짐

Architecture

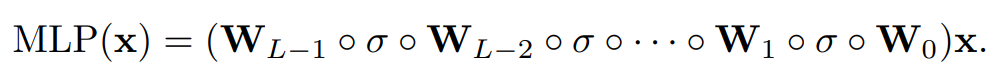
• MLP는 W로 선형변환을 수행하고, σ로 비선형성을 부여한다.
  
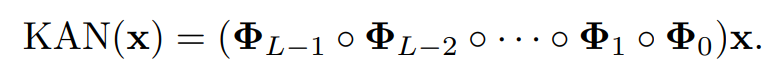
• KAN에서는 이러한 선형변환과 비선형성을 Φ에 통합한다.
• 구체적으로, 고정된 단변량함수(e.g silu)를 B-spline 곡선으로 변환함으로써, 비선형성을 부여하게 된다.

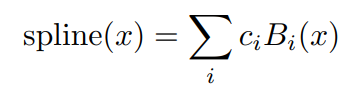
• Φ 는 활성함수 b(x) = silu 와 스플라인 함수의 합으로 구성됨
• 활성함수 b(x) = silu(x) 를 사용
• 스플라인 함수 spline(x) 는 여러 B-스플라인 기저 함수의 선형 결합으로 표현되며, 각 기저 함수는 특정 구간에서만 정의됨.
• Ws : 스플라인함수의 가중치 계수
• Wb : 활성함수의 가중치 계수
• Ci : 스플라인 기저 함수의 계수

Spline 기저 함수 vs Spline 함수

스플라인 기저 함수 : B(x)

• 각 구간에서 정의된 다항식 함수이며, 각 구간에서 미분가능함.
• B(x) 로 기록되며, C0B0(x), C1B1(x) 등으로 나타나짐.
• 즉, Ci는 각 구간에서 정의된 하나의 Spline 기저 함수의 계수 (학습 파라미터)

스플라인 함수

• 여러 스플라인 기저 함수의 선형 결합으로 이루어진 전체 함수.
• Ws(spline(x)) = Ws(C0B0(x) + C1B1(x)) 꼴
• 즉, Ws는 전체 구간에서 정의된 스플라인 함수에 붙는 가중치 계수

Training Process

• 학습 대상은 스플라인 기저 함수의 가중치(Ci), 활성함수의 가중치(Wb), 스플라인 함수의 가중치(Ws) 3가지.
• 손실 함수로는 mse사용
  

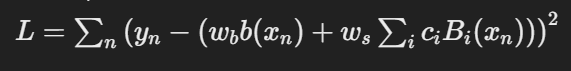
1. 스플라인 차수(k), 격자 점(=경계점) 개수(G) 정의
2. 스플라인 함수는 전체 구간에서 차수 k에 의해 재귀적으로 다항식으로 표현되며, 재귀적으로 생성된 각 다항식에 학습 가능한 파라미터 Ci를 곱하여 각 함수를 학습 가능하도록 설정함. e.g.) Ws(spline(x)) = Ws(C0B0(x) + C1B1(x)) 꼴
3. 격자 점에 의해 전체 구간에서 격자 구간으로 구분(동일한 간격)되며, 경계점을 기준으로 스플라인 함수가 smooth하게 만들어주도록 학습함
4. 학습을 진행하면서, 격자 점은 이동하면서 최적의 곡선을 그림.
   5.. ws, wb, ci를 찾도록 학습

Apporximation Ability

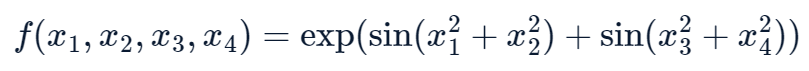
• 다변량 함수 f는 [4,2,1] 총 3개의 KAN layer 로 근사할 수 있으나, 2Layer KAN으로는 activation function을 smooth하게 구성할 수 없음.

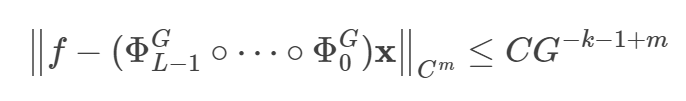
• KAN의 Approximation Boundary는 위 사진처럼 성립한다.
• Boundary를 보면, 입력 차원 N에 의존하지 않는다. 이는 곧 스플라인 함수를 잘 정의하면, 임의의 함수를 잘 근사할 수 있다는 의미이다.

Approximation Boundary

• 해당 수식은 근사 오차의 상한선이다 (Approximation Boundary)
  
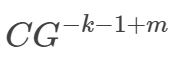
• G^-k : 스플라인 함수의 차수 k가 높을수록, 각 구간에서 높은 차원의 다항식으로 근사할 수 있다. 따라서, k가 클수록 오차가 감소하여 해당 term이 추가된다.
• G^-1 : 격자 크기 G가 커질수록 구간의 길이는 작아지며, 더욱 세밀한 근사가 가능해진다. 따라서, G가 커질수록 오차가 감소하여 해당 term이 추가된다.
• G^m : m차 미분의 연속성을 유지하는 파라미터. 스플라인 함수의 매끄러움 요구 차수라고도 볼 수 있음. 스플라인 함수를 매끄러운 함수로 만들기 위하여 m차 미분까지 고려해야한다는 의미. 따라서, m이 클수록 매끄럽게 만들기 힘들다는 의미이며, 이는 곧 오차가 커진다는 것을 의미하여, 해당 term이 추가됨.

Scaling law

• KAN에서는 매개변수 N이 증가할 때, test loss l은 다음과 같은 규칙으로 감소함.
  
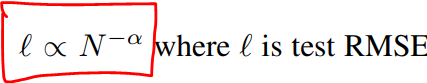
• 알파는 scaling factor
• KAN은 알파값이 커서 더 큰 모델 크기로 성능이 더 빠르게 향상됨

MLP vs. KAN

• MLP
  • UAT에 기반하여 고차원 함수를 근사하지만, data가 sparse해지는 차원의 저주(COD) 문제가 발생할 수 있음
  • 알파값이 낮아 모델 크기가 커질 때 성능 향상이 느림
• KAN
  • COD 문제 극복, 효율적으로 고차원 함수 근사 가능
  • 알파값이 커 모델 크기가 커질 때 성능 향상이 큼

3. Advancement

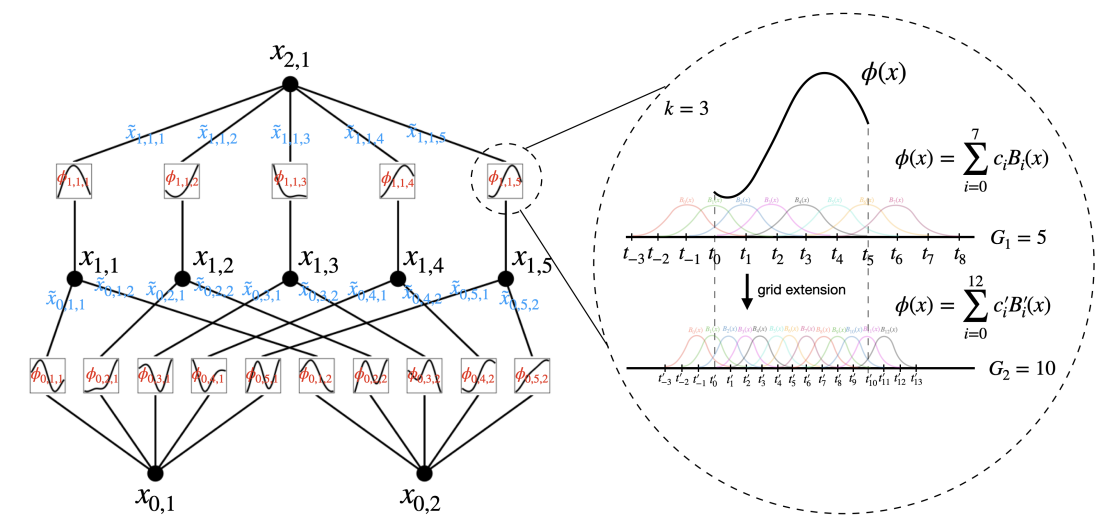
Grid Extension

• 스플라인 기저 함수의 정확도를 높이기 위해 격자 점의 개수를 증가시킴
• 격자 점의 개수를 추가하여 스플라인 기저 함수가 보다 세밀하게 데이터를 근사함

  1. 초기에 지정한 격자 점(G)에서 학습을 진행하면서 격자 점을 추가해나감
  2. 새로운 격자 점을 추가하고, 스플라인 기저 함수의 계수(Ci)를 Update
  3. 똑같이 RMSE를 Loss function으로 사용
     

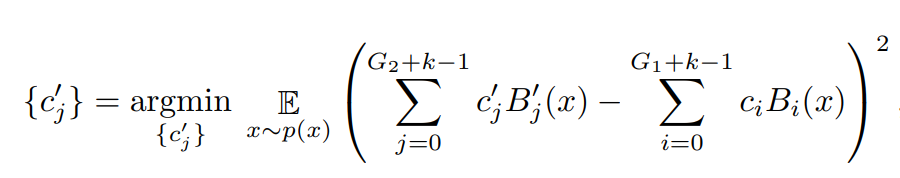
Compressing

• 모델의 밀도를 낮춰 계산 효율성을 높이고, 해석력을 증가시킴

  1. 큰 KAN 모델 정의
  2. Regularization term 을 부여하여 모델을 학습
  3. 중요도 값이 특정 수치 이하인 노드와 엣지를 Pruning
  4. Pruning된 모델을 다시 원래 KAN 꼴로 복원

Regularization

• Define L1 Norm
  
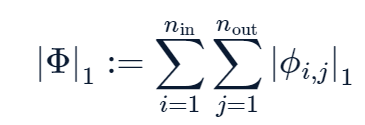
• Define Entropy
  
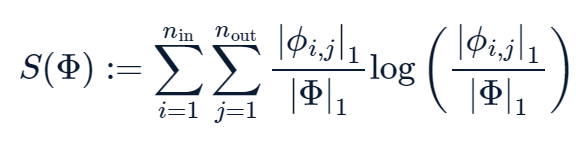
• Loss function에 regularization term을 부여하여 학습
  

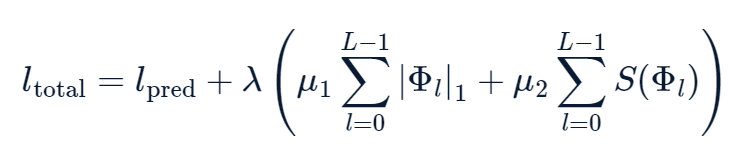
Pruning

• Regularization 이후, 모델을 학습한 뒤, 각 Φ 의 norm을 계산하여 이를 다음과 같은 incoming / outgoing score으로 중요도 측정
• 중요도가 특정 수치 이하라면, 제거