[논문리뷰] Compositional Embeddings Using Complementary Partitions for Memory-Efficient Recommendation Systems 설명
추천시스템
facebook(meta)에서 작성한 논문. KDD 2020 게재
매우 큰 임베딩 테이블을 저장해야할 때, 단순 해싱과 다르게 unique한 임베딩을 보존하면서 크기는 줄이는 방법을 제안
0. Abstract
- 딥러닝 기반의 추천 모델은 여러 범주형(categorical) 변수를 사용하며, 각 범주형 변수는 수백만개의 범주를 가지고 있는 경우가 많다. 일반적으로 각 카테고리(범주)는 하나의 임베딩에 대응시켜 사용한다.
- 범주형 변수도 많고, 각 변수가 수백만 개의 범주를 가지고 있기 때문에 학습/서빙 시점에 메모리의 병목이 되는 경우가 많다.
- 이 논문은 범주형 변수를 보완적인 집합(complementary partition)으로 나눠서 임베딩 테이블의 사이즈를 줄이면서 여전히 각 카테고리별로 unique embedding을 보존할 수 있도록 하는 방법을 제안한다.
- 여러개의 작은 임베딩 테이블을 사용하여 메모리 크기는 줄이면서 범주별로 unique embedding은 유지할 수 있게 된다.
- 기존에 많이 사용되는 해싱처럼 파라미터 갯수는 줄이는 동시에 해싱 대비 높은 성능을 보임을 확인한다.
1. Introduction

- 딥러닝 기반의 추천 모델들은 매우 많은 수의 범주형 변수를 다룬다.
- 예를 들어 사용자, 게시물, 페이지 등의 각각이 범주형 변수가 되며 해당 변수는 수천개의 범주를 가지는 경우가 많다.
- 이러한 범주형 변수는 일반적으로 임베딩 공간으로 매핑되어 dense feature 형태로 사용된다.
- 카테고리의 집합을 , 그 갯수가 라 할 때, 임베딩 테이블 는 와 같다
- 일반적으로 임베딩 테이블은 모델과 함께 학습된다.
- 범주형 변수는 수백만, 수천만개의 매우 큰 범주를 가지게 되는 경우가 있다. 이 경우 임베딩 테이블의 사이즈는 매우 커지며 해당 테이블만으로 수십 GB가 필요한 경우가 발생한다. → 메모리 병목의 원인
- 이러한 사이즈를 줄이기 위해 일반적을 hash function을 사용한다. 이 경우 카테고리의 갯수는 크게 줄일 수 있으나, collision으로 인해 서로 다른 특성을 가지는 변수가 같은 임베딩을 가지게 되어 모델 성능이 급감할 수 있다.
- 극단적인 경우는 취향이 정반대인 사용자가 동일한 임베딩으로 매핑될 수도 있다.
- 가장 이상적인 상황은 임베딩 테이블의 크기는 줄이면서 각 카테고리가 unique 임베딩을 가질 수 있는 것이다.
- 이 논문은 보완적인 집합(complementary partition)으로 범주를 나눠서 compositional embedding을 만든다. 이를 통해 여러 개의 작은 임베딩들을 사용하여 최종 임베딩을 만든다.
- 범주형 변수 그 자체의 특성을 이용할 수도 있지만, 이 논문은 직접적으로 특성을 이용하지 않고도 이를 가능하도록 한다.
- DLRM, DCN(deep cross net)에 적용하여 본다.
- 여기서 제안되는 방법은 적용하기 매우 간단하며, 추가적인 전처리/후처리를 요구하지 않는다. 그러면서도 hashing보다 좋은 성능을 보인다.
1.1 Main Contributions
quotient-remainder trick을 제안한다.. 이는 임베딩 테이블의 사이즈를 줄이면서 여전히 각 카테고리별로 unique embedding을 보존할 수 있도록 한다.- 몫/나머지를 활용하여 서로 다른 두 개의 임베딩 테이블을 만들고 이 둘을 결합하여 최종 임베딩(compositional embedding)을 만든다.
- →로 파라미터 갯수를 줄일 수 있다.
quotient-remainder를 일반화한compositional embedding을 제안한다. 이는 complementary partitions로 카테고리 집합을 분류하는 방식으로 동작한다. 각 카테고리는 적어도 하나 이상의 부분집합에서 서로 겹치지 않도록 각 부분집합으로 분류된다.- 이 경우 파라미터 갯수는 로 줄어든다
- 해싱처럼 collision이 없기 때문에 실험적으로 해싱 대비 높은 성능을 보였다.
- 최종적인
compositional embedding을 만드는 연산 방식은 여러개가 있을 수 있지만, element-wise multiplication이 일반적으로 가장 효과적이었다.- 해당 embedding을 그대로 feature로 사용할 수도 있긴 하다. sparse feature라고 하는 걸 보니 one hot 형태로 변환해서 사용하는 걸 의미하는 것 같다.
- 최종적인
2. QUOTIENT-REMAINDER TRICK(몫-나머지)
-
일반적으로 각 카테고리는 아래처럼 임베딩으로 매핑된다.
- 카테고리를 인덱스로 매핑하는 함수 이
- 임베딩 행렬
- i번째 카테고리를 로 매핑하여 임베딩 값 를 얻는다.
- 혹은 단순 embedding lookup으로 볼 수도 있다.
-
위 과정에서 에 해당하는 메모리 복잡도가 발생하며 카테고리가 많을 수록 그 정도는 커진다.
-
기존에는 임베딩 테이블 크기를 줄이기 위해 hashing을 사용했으며 나누기의 나머지를 이용하는 경우가 많았다.

- embed해야하는 카테고리의 총 갯수
|S|가 있을 때, 해당 카테고리의 인덱스를 해싱 테이블의 크기 m으로 나눠준 나머지가 해당 카테고리의 해싱 테이블에서의 위치이다. - 이때 embedding matrix size는→로 줄어든다.
- 쉽고 좋은 방법이지만, 여러 카테고리를 무지성으로 동일한 임베딩 벡터를 사용하게 만든다는 단점이 있다.
- 카테고리와 임베딩이 일대일 대응이 되지 않는 것이 문제이다.
- embed해야하는 카테고리의 총 갯수
-
나머지만으로는 원래 값과 일대일 대응이 안되지만, (몫,나머지)는 일대일 대응이 가능하다. → 임베딩 테이블을 만들 때 몫도 사용하자!

- 나머지에 해당하는 임베딩 테이블, 몫에 해당하는 임베딩 테이블 두 개에서 각각 임베딩을 뽑은 뒤, 이를 성분곱(element-wise multiplication)하면 카테고리별로 unique embedding을 얻을 수 있다.
- 성분곱이 아닌 다른 pooling 방법을 써도 된다. 더해도 되고 concat도 되고, uniqueness만 보장되는 방식이면 가능하다.
- 수식으로는 아래 형태로 쓸 수 있다.
- 임베딩 행렬 크기는 가 되어 hashing보단 약간 크지만, 대신 unique embedding을 얻을 수 있다.
- 나머지에 해당하는 임베딩 테이블, 몫에 해당하는 임베딩 테이블 두 개에서 각각 임베딩을 뽑은 뒤, 이를 성분곱(element-wise multiplication)하면 카테고리별로 unique embedding을 얻을 수 있다.
3. COMPLEMENTARY PARTITIONS
-
quotient-ramainder는 complementary partition의 한 예일 뿐이다. 이 방법은 전체 category의 특정 부분집합(bucket)을 원소로 가지는 partition 여러 개를 결합하는 방식이다.
-
같은 부분집합(bucket)에 속한 카테고리들은 해당 집합에 대응되는 embedding matrix에서 같은 vector를 갖는다. 즉, 해싱은 이러한 partition 하나로 카테고리들을 분류하는 것이라 볼 수 있다.
-
이 partition 여러개를 결합했을 때, 모든 partition에서 같은 부분집합(bucket)에 속하는 카테고리가 없다면 이는 complementary partition이다.
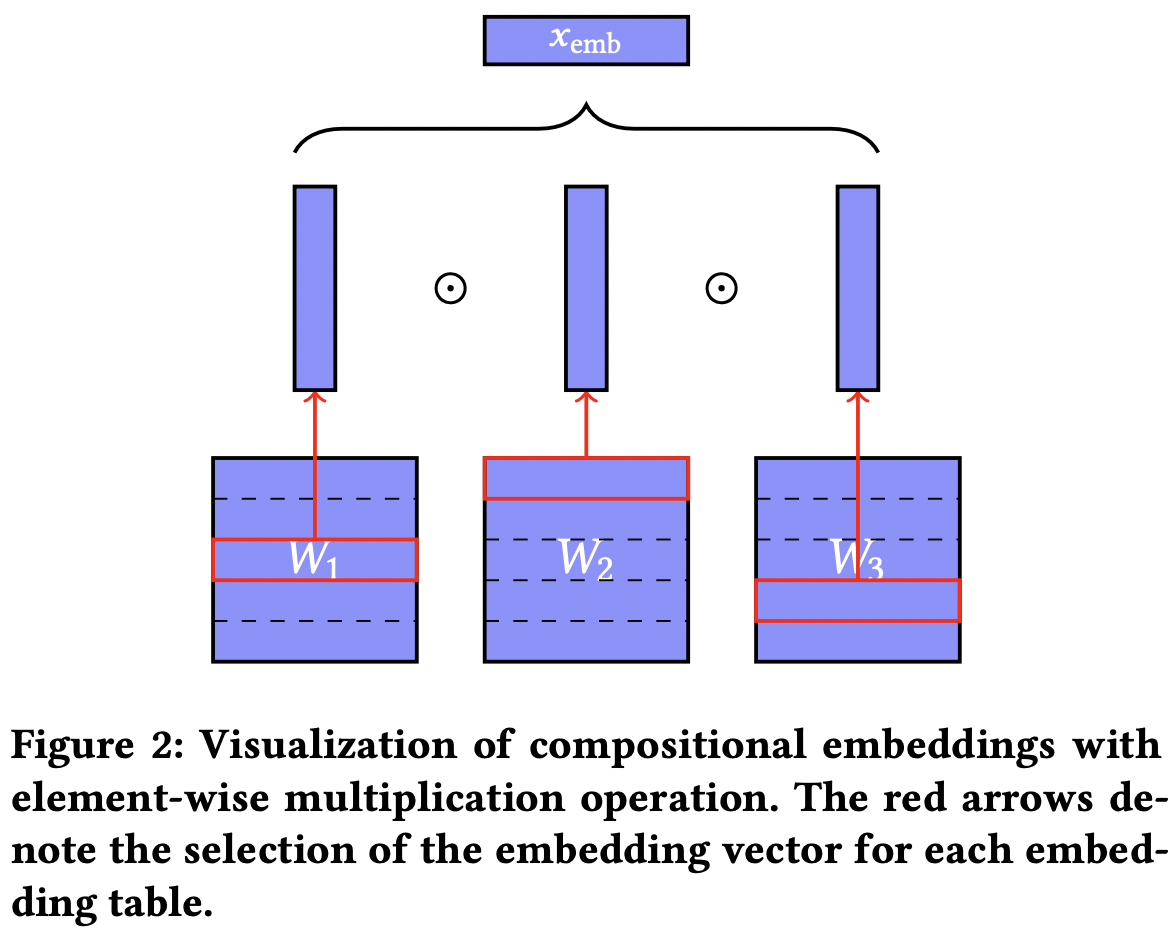
- 📖 Definition 1. Given set partitions of set S, the set partitions are complementary if for all such that , there exists an i such that
- e.g. 에 대해 아래 세 개의 partition은 complemantary하다.
-
각 partition은 하나의 임베딩 행렬에 대응되고, bucket은 해당 행렬의 벡터 하나에 대응된다.
-
3-1. Examples of Complementary Partitions
위에 나온 quotient-remainder trick보다 일반화된 형태로도 구성할 수 있다.
(1) Naive Complementary partition
- 그냥 기존의 임베딩 행렬도 partition 하나짜리인 complementary partition으로 볼 수 있다.
(2) Quotient-Remainder Complementary Partitions
- 위에 언급한 몫-나머지 쌍을 활용하는 방법

(3) Generalized Quotient-Remainder Complementary Partitions
- 에 대하여 를 만족할 때 아래처럼 complementary partition을 정의할 수 있다.
-
- 즉, 몫에 대해서 다시 나머지를 구하는 과정을 반복한다. 단순 몫-나머지 쌍을 좀더 일반화한 형태이다.
- 잘 조절하면 단순 quotient-remainder보다 파라미터 수를 줄일 수도 있다.
(4) Chinese Remainder Partitions
- 이 부분은 사실 잘 이해가 되지 않았다. 하지만 어차피 원리는 비슷하기 때문에 이보단 앞의 것들을 쓰는 게 좋아보인다.

(번외) meta 정보를 활용할 수도 있다. 예를 들면 자동차의 경우, 제조사/제조년/제조지 등등을 결합하면 complementary partition을 만들 수도 있을 것이다.
4. COMPOSITIONAL EMBEDDINGS USING COMPLEMENTARY PARTITIONS
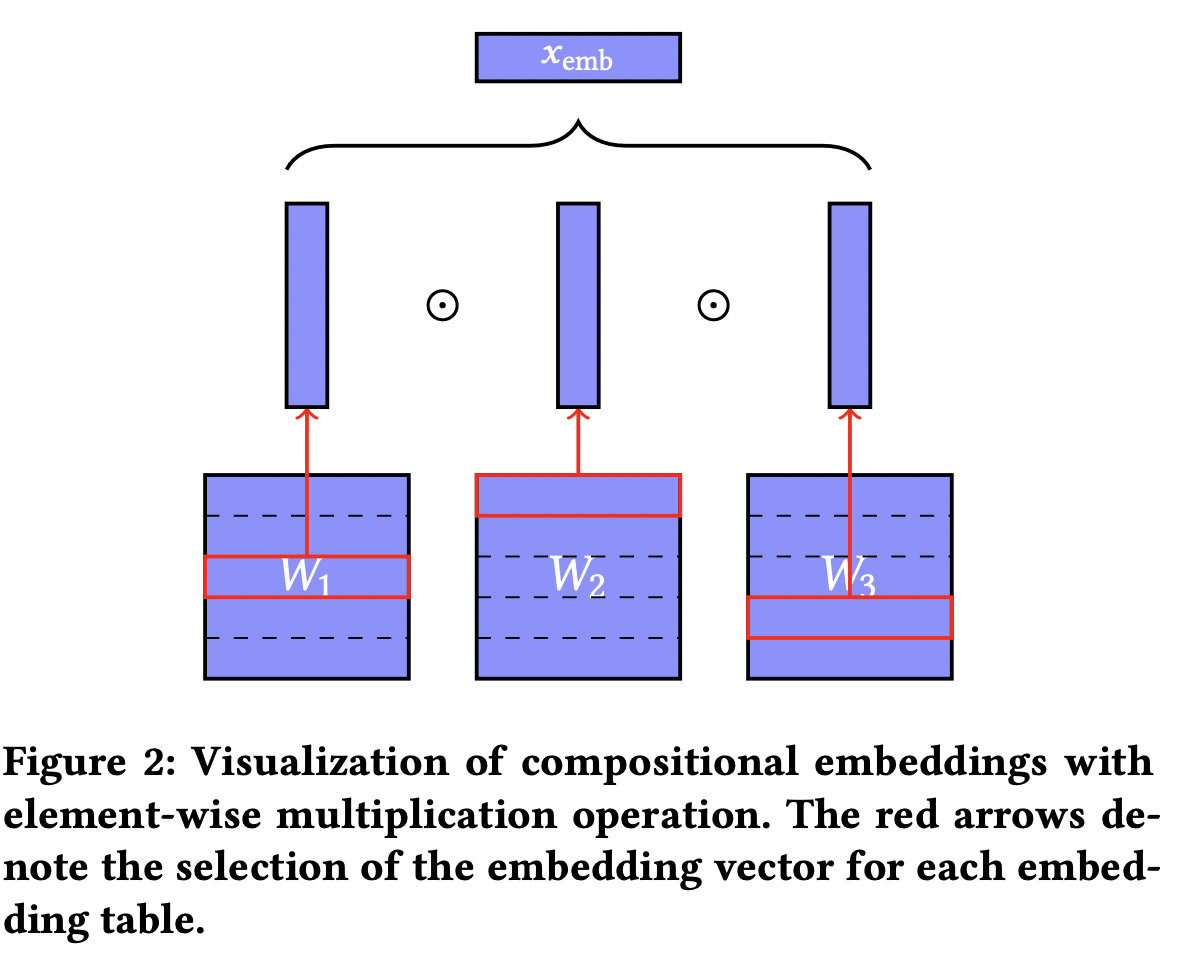
- 위의
complementary partition들은 각각 임베딩 행렬에 대응된다. 여기서 얻은 임베딩 백터들을 특정 연산(e.g. 성분곱)으로 합칠 수 있다.- 특정 카테고리가 각 partition에서 해당하는 bucket을 정수 형태의 index()로 나타내면 아래처럼
operation-based compositional embedding을 만들 수 있다. - 위에서 w는 백터들에 대한 연산을 나타내며, 대표적으로 아래 방법들을 사용할 수 있다.
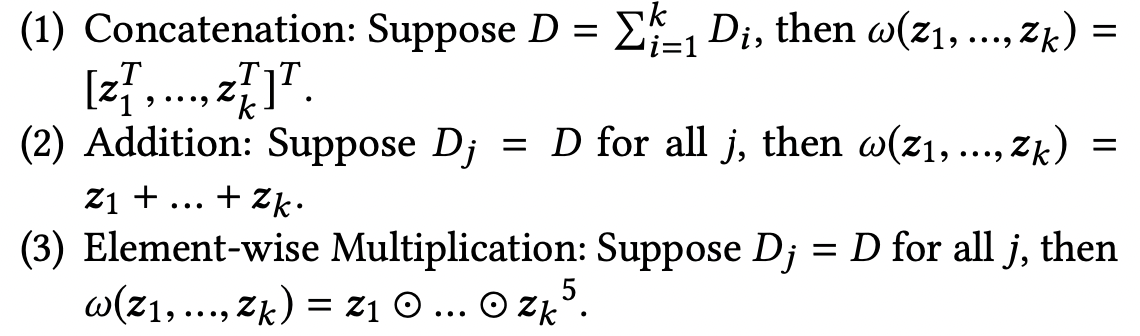
- 특정 카테고리가 각 partition에서 해당하는 bucket을 정수 형태의 index()로 나타내면 아래처럼
- 위 방법을 사용하면 특정 가정하에서 모든 카테고리가 unique embedding을 가짐을 보일 수 있다. 증명도 있으나, 굳이 증명까지 볼 필요 없이 직관적으로 이해되는 부분.

- 이처럼 complementary partition을 활용하여 compositional embedding을 만들 경우, 아래처럼 embedding matrix의 메모리 복잡도를 줄일 수 있다.
- 이고, 를 임의로 고를 수 있다면 memory 복잡도는 로 최적화할 수도 있다.
4-1. Path-Based Compositional Embeddings

- 위의 complementary partition을 활용한 compositional embedding 은 initial embedding을 함수의 composition으로 변환하는 것으로 생각할 수 있다.
- 즉, 2번 이후의 partition embedding에 대한 element-wise multiplication을 일종의 함수라고 생각할 수 있다.
- 그렇다면, 다른 함수도 사용해도 될 것이다.
- 모든 partition에서 embedding을 정의하지 말고, 첫 번째 partition에서만 embedding을 정의한 뒤 나머지 partition은 각각에 대응되는 함수를 정의한다. 첫 번째 embedding이 이를 연쇄적으로 통과한 결과, unique한 embedding이 만들어진다. ⇒ 이를
path-based compositional embedding이라 한다.- 첫 번째 partition에 대응되는 정의.
- 2번째 이후 partition에 대응되는 함수의 집합 정의
- 각 partition에 대한 bucket 매핑
- 최종 임베딩 생성
- 즉, 각 complementary set의 부분집합에 대응되는 함수가 있으며 이를 composition of function으로 엮을 수 있다. 이를
path-based compositional embeddings라 한다. 이때 각 함수에 해당하는 parameter 역시 학습되어야 하며 아래와 같은 방법들을 사용할 수 있다.
- 이제 2번 이후의 partition에 대해 embedding matrix가 존재하지 않아도 되기 때문에, composition할 함수를 어떻게 설정할지에 따라 parameter 사용 갯수가 크게 줄 수도, 혹은 오히려 증가할 수도 있다.
- MLP를 사용하며 크기를 잘 조절하면 의 메모리 복잡도를 얻을 수 있다.
5. Experiments
- quotient-remainder trick이 파라미터 갯수를 해싱만큼 줄이면서 기존 모델의 정확도를 달성할 수 있음을 보인다.
- DCN과 페이스북의 DLRM을 활용한다.
5-1.Model specification
- DCN 세팅
- [512, 256, 64] 3개의 hidden layer 가진 deep network
- 5개의 layer로 구성된 cross network
- 16차원의 범주형 변수 임베딩
- DLRM 세팅
- [512, 256, 64] 3개의 hidden layer 가진 bottom MLP
- [512, 256] 2개의 hidden layer 가진 top MLP
- 16차원의 범주형 변수 임베딩
- baseline(full embedding) 모델의 경우 범주의 갯수만큼 크기를 갖는 임베딩 테이블을 사용함
5-2. Experimental Setup and Data Pre-processing
- Criteo의 kaggle 데이터를 활용함
- 13 dense feature, 26 categorical feature 가짐
- 7일간의 4500만건의 데이터
- 6일로 학습 7일차는 validation과 test set으로 활용
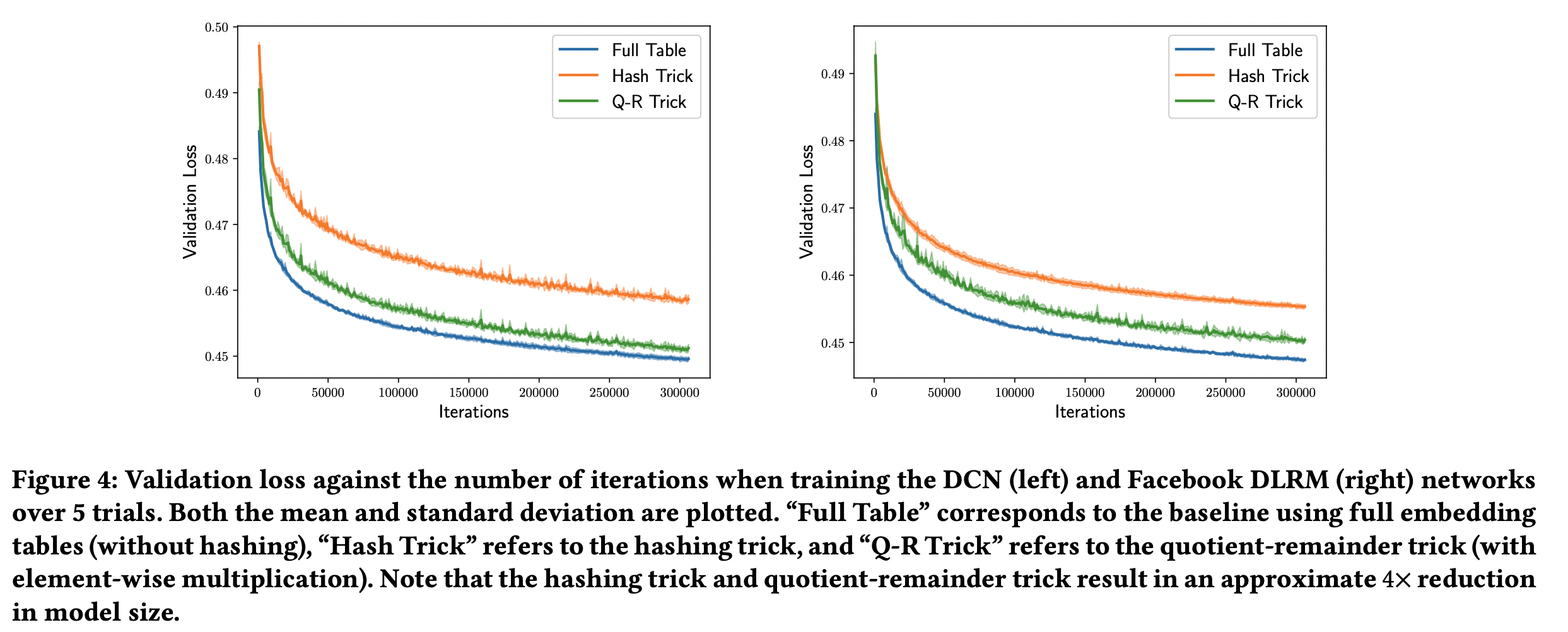
- full model / hashing model / quotient-remainder with element-wise multiplication 비교
- hashing model과 quotient-remainder의 경우 모델 사이즈가 full 모델 대비 1/4이 되도록 조절함
- 즉, hashing의 경우 4개의 hash collision이 발생하도록 했음
- 5번의 실행에 대한 평균/표준편차를 시각화 함
- quotient-remainder가 hashing trick의 경량화와 full model의 성능 사이에서 적절한 균형을 찾음을 위의 fig-4에서 확인할 수 있었다.
5-3. Compositional Embeddings
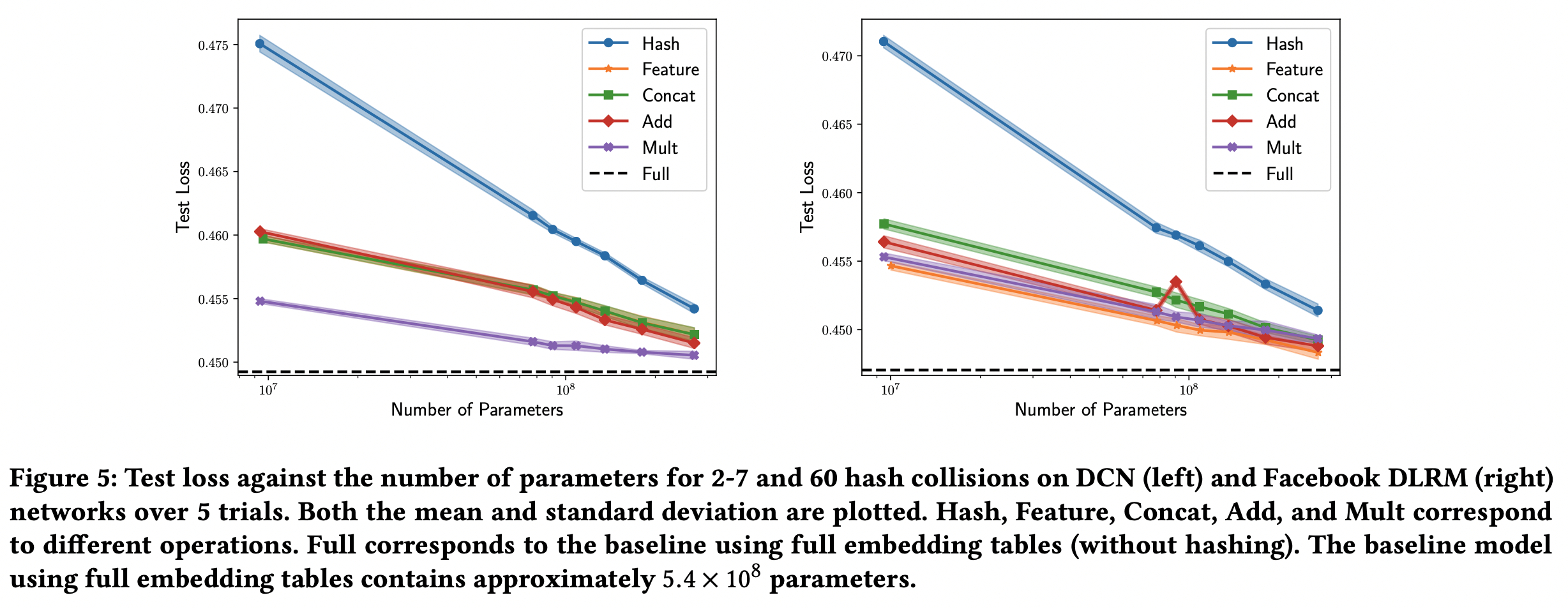
-
hash collision의 크기와 test loss 간의 관계를 그려보았다. embedding table의 파라미터가 전체 모델 파라미터의 대부분을 차지하기 때문에 모델 크기와의 관계라 볼 수도 있다.
- 마찬가지로 QR embedding도 파라미터 갯수를 비슷하게 맞췄다
-
QR의 경우 곱하기 연산이 DCN에서는 가장 좋았고, DLRM에서도 두 번째로 좋았다. 즉 여러모로 제일 낫다.
- 참고로, multiplication의 경우 Adagrad보다 AMSGrad를 사용할 때 훨씬 크게 성능이 향상되었다.
-
4개의 hash collision으로 얻은 성능이 60개의 hash collision 만큼 parameter 감소시킨 QR embedding에서 달성 가능했다. 즉 매우 작은 모델로도 hashing을 이겼다.
-
각 범주형 변수 중 카테고리의 갯수가 특정 임계값 이상인 경우에만 hashing/QRembedding을 사용하는 경우도 생각해볼 수 있다.
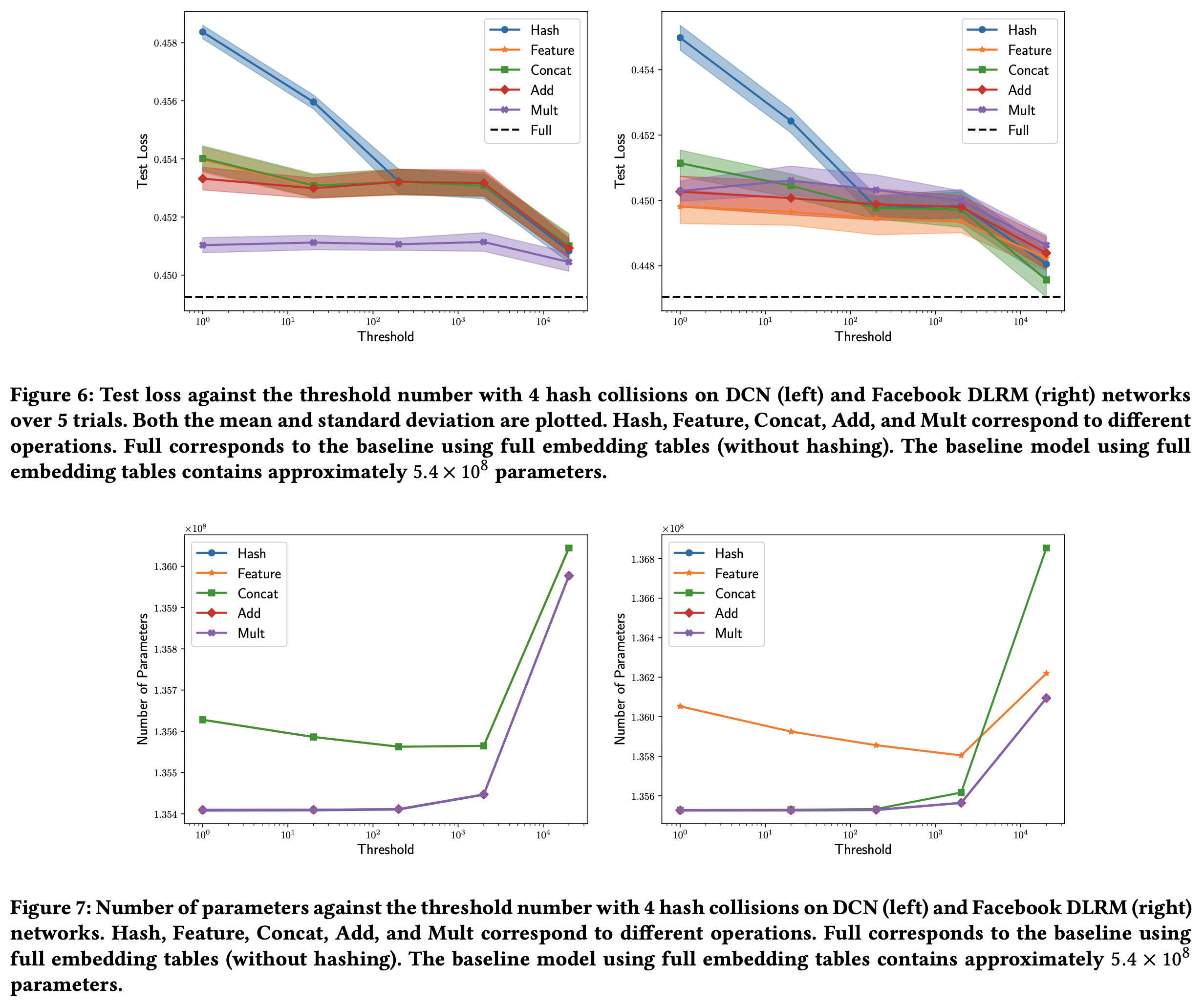
- 4개의 hash collision으로 제한한 상태에서 임계값을 {1, 20, 200, 2000, 20000}로 각각 그려보았다.
- 이 경우 DCN에선 성분곱이 제일 좋았고, DLRM에선 concat이 제일 좋았다.
- 모델들 간의 차이가 좀더 줄어들었다.
- 4개의 hash collision으로 제한한 상태에서 임계값을 {1, 20, 200, 2000, 20000}로 각각 그려보았다.
5-4. Path-Based Compositional Embeddings
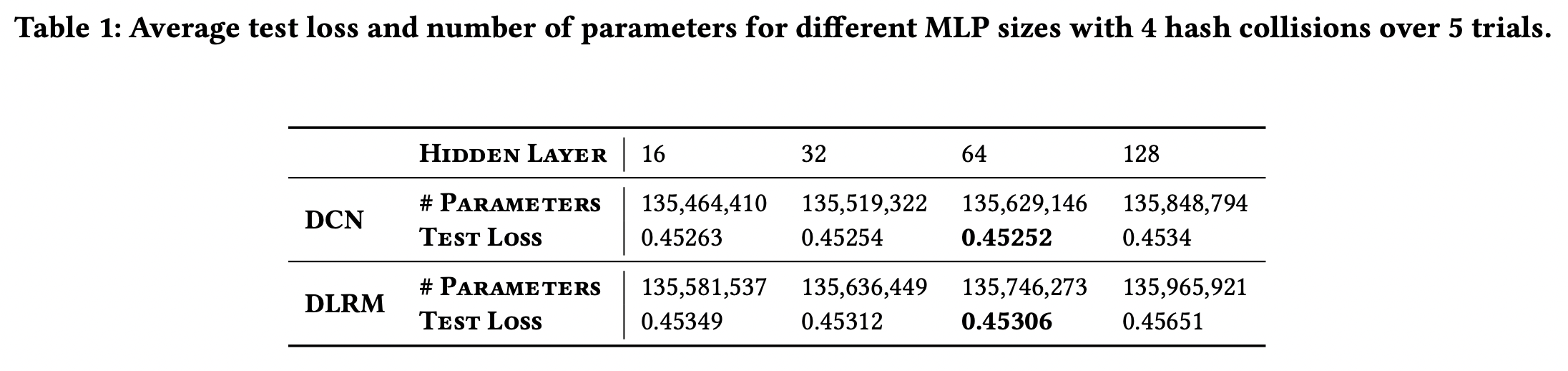
- MLP를 활용한 path-based compositional embedding으로 평가해보았다.
- 4개의 hash collision으로 고정하고, 16, 32, 64,128 사이즈의 single hidden layer MLP로 평가했다.
- 결과
- 64 차원이 가장 성능이 좋았다. 작으면 충분한 transform이 되지 못하고, 너무 크면 파라미터 갯수가 충분히 줄어들지 못했다.
- 위까진 DLRM이 무조건 성능이 더 좋았는데 MLP를 사용하니 DCN이 성능이 더 좋아졌다.
5-5. Discussion of Tradeoffs
- 모델 크기를 줄이면 메모리 이점은 있으나 성능이 줄고, 반대의 경우 역전된다.
- 모델의 성능은 partition이 실제 해당 카테고리의 특성을 얼마나 잘 반영하는가에 의존성이 있다. 따라서 해당 특성을 잘 반영하도록 partition을 만들면 더 좋을 것이다.
- 적어도 hashing처럼 무지성 collision은 아니고 unique embedding은 보장되니 아주 약간의 추가적인 메모리 사용으로 성능은 크게 늘릴 수 있다.
- operation-based compositional embedding은 path-based에 비해 상대적으로 단순하다고 생각되기 때문에 좀더 어렵고 꼬인 문제에선 path-based가 좋을 것이라 생각되었다.
- 하지만 이번 실험에선 operation-based가 더 좋았으나, 추후 path-based가 더 좋게 활용되는 사례들이 등장될 거라 생각된다.