계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.
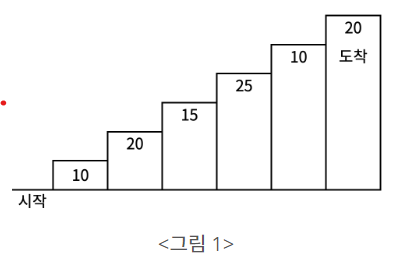
예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.
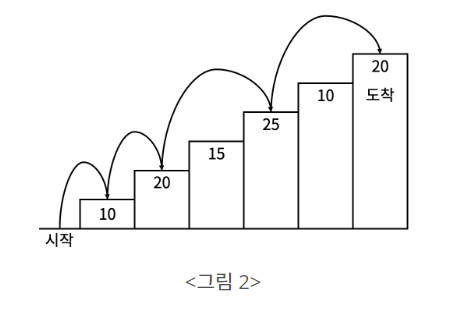
계단 오르는 데는 다음과 같은 규칙이 있다.
계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
DFS로 잘못 푼 코드
import sys
sys.stdin = open("input.text", "rt")
sys.setrecursionlimit(10**6)
#한 계단 or 두 계단
#연속된 세 개의 계단을 밟을 순 없다
#도착 계단은 밟아야 한다.
n = int(input()) #계단의 개수
data = []
for _ in range(n):
data.append(int(input()))
res = 0
def DFS(L, check, sum):
global res
if L ==n: #종료조건
if res < sum:
res = sum
else: # 계속 선택 한 계단 or 두 계단
if check != 2: #아직 2연속 아니야
DFS(L+1, check + 1, sum + data[L])
if L+2 <= n: #두 계단 점프 가능
DFS(L+2, 0, sum + data[L])
else: #check == 2 라면 3연속 안됨
if L+2 <= n:
DFS(L+2, 0, sum + data[L])
DFS(0,0,0)
print(res)dp로 제대로 푼 코드
import sys
sys.stdin = open("input.text", "rt")
sys.setrecursionlimit(10**6)
#한 계단 or 두 계단
#연속된 세 개의 계단을 밟을 순 없다
#도착 계단은 밟아야 한다.
n = int(input())
data =[-1] #1번 인덱스부터 사용하기 위해.
for _ in range(n):
data.append(int(input()))
if n == 1:
print(data[1])
exit(0)
dp = [0] * (301) #dp 테이블은 그래도 좀 많이 만들어놓고 풀자
dp[1] = data[1]
dp[2] = data[1] + data[2] #자명한 사실.
for i in range(3,n+1):
caseA = dp[i-3] + data[i-1] + data[i]
caseB = dp[i-2] + data[i]
dp[i] = max(caseA, caseB)
print(dp[n])⚽ 코멘트
처음에 조건이 연속 3계단이 안된다고 해서, dp로 풀기에는 조건을 어떻게 해야할지 몰라서 DFS로 푸는게 낫다고 생각했다.
- 근데 시간초과... 일단 코드는 맞는 것 같은데 사실 코드가 맞는지도 모르겠다.
어쩃든 dp로는 어떻게 풀어야할지 몰라서 다른 사람들의 답을 보았다. (아직 dp 어떻게 풀어야할 지 감을 못잡음...)
- dp 테이블은 일단 초반에 좀 크게 만들어 놓자.. (그래야 혹시 모를 예외를 풀 수 있음)
dp[1]에는 당연히 첫번째 점수가 들어간다. (자명한 값은 미리 초기화하자)
이제 dp의 생각의 시작. 즉 작은 문제를 점진적으로 확장해 나가보자.
- 첫번째 계단까지는 당연히 첫번째 계단만 밟는게 최대.
- 두번째 계단까지는 첫번째 + 두번째 계단의 합이 최대.
- 세번째 계단부터가 이제 핵심인데, 세번째 계단으로 올 수 있는 경우는 -1 지점에서 오는 것, -2지점에서 오는 것 두가지이다.
⚽ 도착지점을 end라고 할 때 end-1을 밟을 경우 end-2계단은 밟으면 안된다.
⚽ end-2를 밟을 경우 이전 계단 신경 안써도 된다.
이걸 이제 점화식으로 표현하면, dp[i]는 i번째 계단까지의 최댓값인데
- i-2번째 계단까지의 최대 가중치 합 + 현재 계단 가중치
- i-3번째 계단까지의 가중치합 + i-1번째 계단의 가중치 + 현재 계단의 가중치
이 두개의 값 중 큰 것을 저장할 수 있다 !!!
👻 이 점화식을 문제풀 때 생각할 수 있었어야 했는데... dp문제 많이 연습하자.
- 이 문제는 다시 풀어보기
👻 백준 dp 문제를 풀다보면 런타임에러가 자주 나온다. 그 이유를 생각해보면 미리 dp테이블을 만들어 놓고 해당 값을 저장하는데,
- 위 문제처럼 dp[1] = data[1], dp[2] = data[1] + data[2]
- 이런 식으로 저장을 하는데, 만약 n == 1인 경우 인덱스 에러가 뜬다.
- 그렇기에 이런 n이 작을 때의 런타임 에러를 생각해서 초반에 예외처리 해주자 !!! + dp 테이블은 기본적으로 어느정도 크게 잡는게 좋은듯