Single-layer Perceptron(단층 퍼셉트론)

1. What is perceptron🙄❔

퍼셉트론은 1957년 Cornell Aeronautical Lab의 Frank Rosenblatt에 의해 고안된 인공신경망이다. 로젠블라트에 의해 제안된 것은 가장 간단한 형태의 단층 퍼셉트론(single-layer perceptron)으로 입력 벡터를 두 부류로 구분하는 선형분류기이다.
이는 신경망(딥러닝)에 기원이 되는 알고리즘이다. 퍼셉트론은 다수의 신호(흐름이 있는)를 입력으로 받아 하나의 신호를 출력한다. 퍼셉트론은 이 신호를 입력으로 받아 '흐른다/안 흐른다'(1 또는 0)이라는 정보를 앞으로 전달한다.

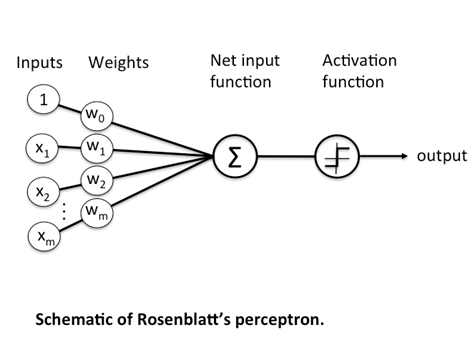
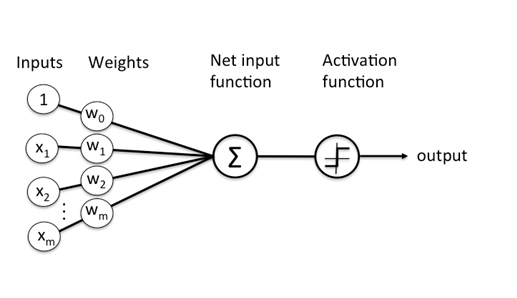
위의 그림에서,
◾$x_1$과 $x_2$는 입력 신호, $y$는 출력 신호, $w_1$과 $w_2$는 가중치(weight)를 의미한다.
◾원을 뉴런 또는 노드라고 부른다.
◾입력 신호가 뉴런에 보내질 때는 각각 고유한 가중치가 곱해진다($x_1w_1,x_2w_2$).
◾뉴런에서 전달 받은 신호의 총합이 임계값 $\theta$를 넘을 때만 1을 출력한다.

2. 용어 정의

용 어	정 의
임계치(threshold)	어떠한 값이 활성화되기 위한 최소값을 임계치라고 한다
가중치(weight)	퍼셉트론의 학습 목표는 학습 벡터를 두 부류로 선형 분류하기 위한 선형 경계를 찾는 것이다. 가중치는 이러한 선형 경계의 방향성 또는 형태를 나타내는 값이다.
편향(bias)	선형 경계의 절편을 나타내는 값으로써, 직선의 경우는 y절편을 나타낸다.
net값	입력값과 가중치의 곱을 모두 합한 값으로써, 기하학적으로 해석하면 선형 경계의 방정식과 같다.
활성함수(activation function)	뉴런에서 계산된 net값이 임계치보다 크면 1을 출력하고, 임계치보다 작은 경우에는 0을 출력하는 함수이다. 이 정의는 단층 퍼셉트론에서만 유효하며, 다층 퍼셉트론에서는 다른 형태의 활성함수를 이용한다.
뉴런(neuron)	인공신경망을 구성하는 가장 작은 요소로써, net값이 임계치보다 크면 활성화되면서 1을 출력하고, 반대의 경우에는 비활성화되면서 0을 출력한다. node라고도 한다

3. 단순한 논리회로

AND 게이트

입력이 둘이고 출력이 하나인 대표적인 퍼셉트론으로 나타낼 수 있는 예시는 AND 게이트이다. 아래의 표는 AND 게이트의 진리표이며 이 AND게이트를 퍼셉트론으로 표현해보자. 이를 위해서는 $w_1,w_2,\theta$의 값을 적절하게 정해야 한다.

AND

$x_1$	$x_2$	$y$
0	0	0
0	1	0
1	0	0
1	1	1

단층 퍼셉트론은 값을 보내는 단계과 값을 받아서 출력하는 두 단계로만 이루어졌다. 즉 입력층과 결과층으로만 이뤄진다. 층이 하나라 선형 영역에 대해서만 분류가 가능하다.
AND 게이트를 진리표에 따라 분류하는 선을 그어보면 다음과 같다.

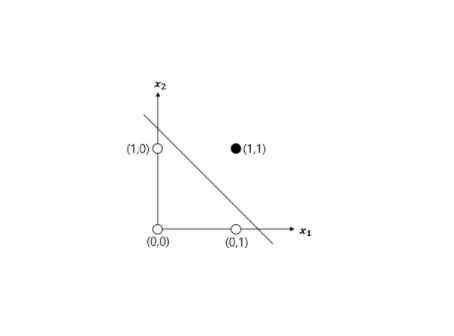
이제 ($w_1,w_2,\theta$) 이 ($0.5, 0.5, 0.7$) 인 경우를 생각해보자.

$(0*0.5) + (0*0.5) = 0.0 < 0.7$ -> $0$

$(0*0.5) + (1*0.5) = 0.5 < 0.7$ -> $0$

$(0*0.5) + (0*0.5) = 0.5 < 0.7$ -> $0$

$(1*0.5) + (1*0.5) = 1.0 > 0.7$ -> $1$

이렇게 AND 게이트의 값을 만족한다.
이러한 ($w_1,w_2,\theta$) 경우의 수는 무수히 많다.

bias(편향)의 도입

일단 $\theta$를 $-b$로 치환하면 퍼셉트론의 동작이 아래와 같은 식으로 만들어진다.

여기서 $b$는 편향(Bias) 이라고 일컫는다.
퍼셉트론은 입력신호에 가중치를 곱한 값과 편향을 합하여, 그 값이 0을 넘으면 1을 출력하고 그렇지 않으면 0을 출력한다.

이를 통해 Python으로 AND 게이트를 구현보면 다음과 같다

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]

for x1, x2 in inputs:
    y = AND(x1, x2)
    print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))

(0, 0) -> 0
(1, 0) -> 0
(0, 1) -> 0
(1, 1) -> 1

지금은 $w$와 $b$의 값을 지정해줬지만, Deep learning에서는 이 값들을 스스로 찾게하는 학습을 하게 된다.

NAND 게이트

NAND 게이트는 AND에 NOT 연산을 한 것이다. (AND 결과에서 0을 1로, 1을 0으로) 즉, AND 게이트의 출력을 뒤집은 것이다. 진리표는 아래와 같다. NAND 게이트도 마찬가지로 진리표의 값들을 만족하는 ($w_1,w_2,\theta$) 순서쌍이 존재한다. 예를 들면 (-0.5, -0.5, -0.7) 이다.

NAND

$x_1$	$x_2$	$y$
0	0	1
0	1	1
1	0	1
1	1	0

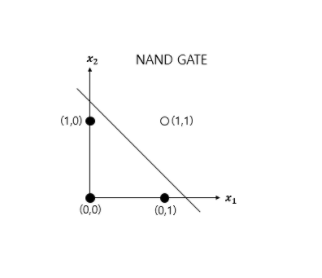
Python으로 NAND 게이트를 구현보면 다음과 같다.

def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]

print('NAND :')
for x1, x2 in inputs:
    y = NAND(x1, x2)
    print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))

NAND :
(0, 0) -> 1
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

OR 게이트

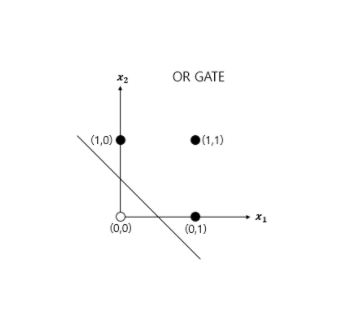
OR 게이트는 입력 신호 중 하나 이상이 1이면 출력이 1이 되는 논리 회로다. 진리표를 짜보면 아래와 같다.

OR

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	1

Python으로 OR 게이트를 구현보면 다음과 같다.

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

inputs = [(0, 0), (1, 0), (0, 1), (1, 1)]

print('OR :')
for x1, x2 in inputs:
    y = OR(x1, x2)
    print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))

OR :
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 1

4. 단층 퍼셉트론의 한계

XOR의 등장

XOR 게이트는 베타적 논리합이라는 논리 회로로 진리표는 아래와 같다.

XOR

$x_1$	$x_2$	$y$
0	0	0
1	0	1
0	1	1
1	1	0

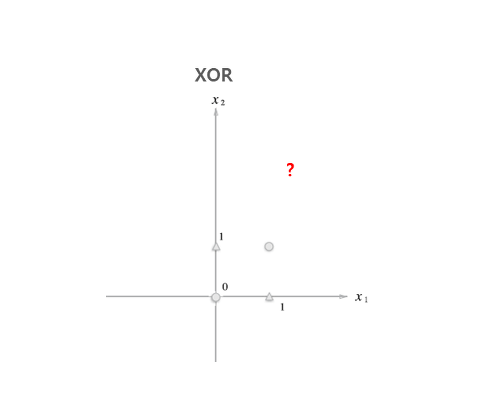
단층 퍼셉트론으로 AND, NAND, OR 게이트는 구현 가능하지만, XOR 게이트는 구현할 수 없다. 퍼셉트론은 앞서 위에서 본 것 같이 직선으로 나뉜 두 영역을 만든다. 하지만 XOR은 직선으로 두 영역을 나눌 수 없다. XOR 게이트로 인해 그 이후로 ‘인공 신경망’과 관련된 연구는 오랜 기간 침체기를 겪었고, 제대로 된 발전을 이루지 못했다.

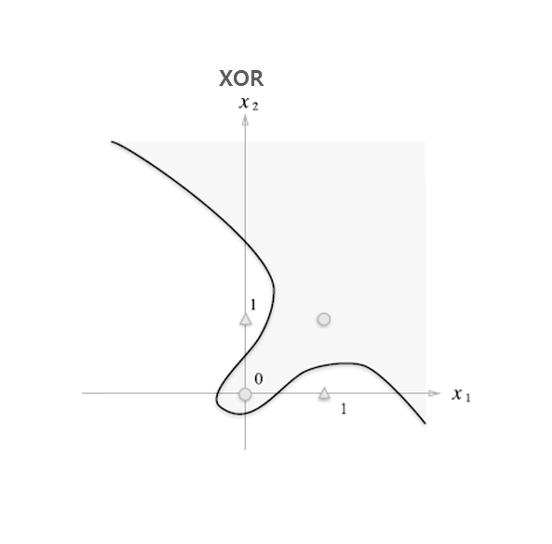
하지만 직선 즉, 선형이라는 제약을 없앤 비선형 이라면 아래와 같이 영역을 나눌 수 있다.

5. 다층 퍼셉트론

단층 퍼셉트론으로는 XOR을 구현할 수 없지만, multi-layer perceptron(다층 퍼셉트론)으로 XOR 게이트를 구현할 수 있다.

먼저, 아래의 그림처럼 입력값 $x_1,x_2$를 각각 NAND 게이트와 OR 게이트에 보낸다음, 그 결과 값들을 AND 게이트에 보내면 XOR 게이트를 구현할 수 있다.


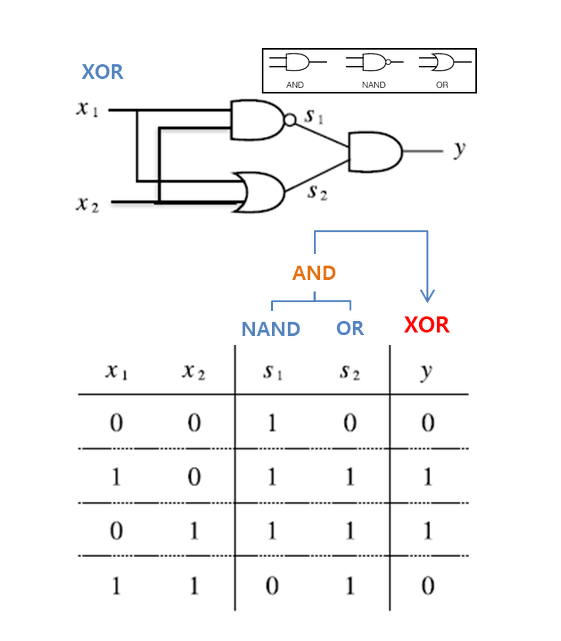
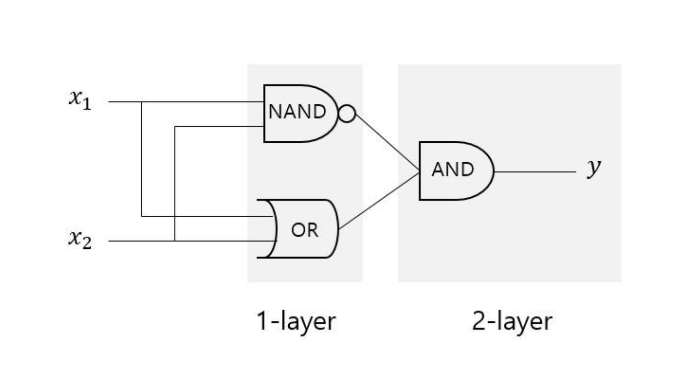
이로써 우리는 XOR 게이트가 두 개의 층으로 구성된 다층 퍼셉트론인 것을 알 수 있다.

마지막으로 Python으로 XOR 게이트를 구현보면 다음과 같다.

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

print('XOR :')
for x1, x2 in inputs:
    y = XOR(x1, x2)
    print('({x1}, {x2}) -> {y}'.format(x1=x1, x2=x2, y=y))

XOR :
(0, 0) -> 0
(1, 0) -> 1
(0, 1) -> 1
(1, 1) -> 0

6.Reference

https://untitledtblog.tistory.com/27
https://eehoeskrap.tistory.com/137
https://excelsior-cjh.tistory.com/169