[algorithm] Building Heap

Building Heap_ bottom-up

• Heap은 bottom-up의 방법으로 하위배열에서 Heapify() 함수를 실행함으로써 만족시킬 수 있습니다.
• 자식이 없는 leaf node는 자동적으로 힙의 속성을 만족하므로, leaf node를 제외 한 나머지 노드들에 대해 순차적으로 Heapify를 수행하면 됩니다.
• 크기가 n인 배열에서 자식의 index범위는 $⌊𝑛/2⌋+1..𝑛]$ 입니다. 따라서, 배열을 거꾸로 거슬러 올라가 $⌊𝑛/2⌋..1]$ 까지 각각의 노드에서Heapify를 수행하면 됩니다.

Pesudo Code

BUILD-HEAP(A,n)

• BUILD-HEAP(A,n) 의 알고리즘은 다음과 같이 동작합니다.

1. $i$ 를 $⌊𝑛/2⌋$ 에서 $1$ 까지 감소시키며 반복합니다
2. 각 반복에서 $HEAPIFY(A,i,n)$ 를 호출하며 부분힙을 최대힙으로 만듭니다.

루프불변성

• 루프불변성이란 루프의 각 반복전에 항상 참인 조건을 의미합니다. 이를 통해 루프가 끝난 후에도 특정조건이 유지됨을 보장할 수 있습니다.

• 루프불면성을 증명하기 위해서 다음의 세가지 단계를 고려해야합니다.

• 1. 초기화 (Initialization): 루프의 첫 번째 반복 전에 불변식이 성립해야 합니다.

• 2. 유지 (Maintenance): 루프의 각 반복 동안 불변식이 계속해서 참이여야 합니다.

• 3. 종료 (Termination): 루프가 종료된 후 불변식이 최종 목표를 만족함을 보이는 단계입니다. 즉, 루프가 끝났을 때 불변식이 문제 해결의 올바른 결과를 보장해야 합니다.

루프불변성_ BUILD - HEAP

• BUILD-HEAP관점에서 루프불변성은 각 반복전에 모든 노드 $i+1, i+2, ... n$ 은 최대힙의 루트이다.

• 초기화 (Initialization)
  루프가 시작되기 전, $i=⌊n/2⌋$ 입니다. 이 시점에서 모든 노드
  $⌊n/2⌋+1,⌊n/2⌋+2,…,n$ 은 리프 노드입니다. 리프 노드는 최대 힙의 속성을 만족합니다. 따라서, 루프가 시작되기 전에 불변식이 성립합니다.

• 유지 (Maintenance)
  루프의 각 반복 동안, $HEAPIFY(A, i, n)$을 호출합니다. 이 함수는 다음과 같은 과정을 통해 노드$i$를 루트로 하는 부분트리가 최대합이 되게 합니다.

• HEAPYFY는 노드 i의 자식노드들이 이미 최대힙의 루트임을 가정합니다

• 노드 i와 그 자식노드들 사이의 최대힙 속성을 위반하는 부분을 수정하여 노드 i를 최대힙의 루트로 만듭니다.

이 과정을 통해, 한번의 HEAPIFY 의 호출이 끝나면, 노드 i와 그 자식노드들은 모두 최대힙의 루트가 됩니다. i를 감소시키고, 다음 반복을 수행하면, 새로운 i와 그 자식노드들도 최대힙의 루트가 됩니다.
따라서, 루프의 각 반복 후에도 불변식이 유지됩니다.

• 종료 (Termination)
  루프가 종료되는 시점은 $i=0$일 때입니다. 이 시점에서 불변식에 의해 모든 노드 $1,2,…,n$ 은 최대 힙의 루트가 됩니다. 특히, 노드 1이 최대 힙의 루트가 되므로 전체 배열 A는 최대 힙으로 정렬됩니다.

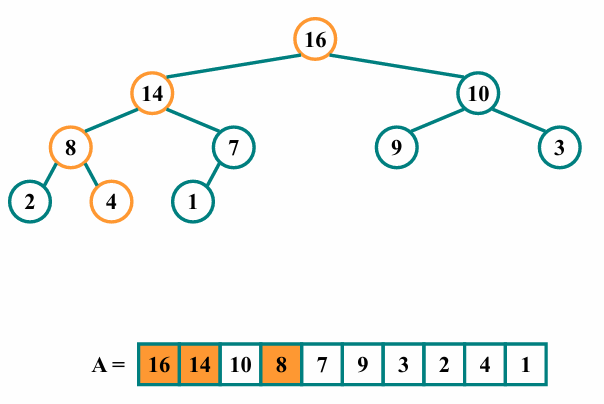
이제 예시를 들어 Building Heap의 과정을 살펴봅시다.

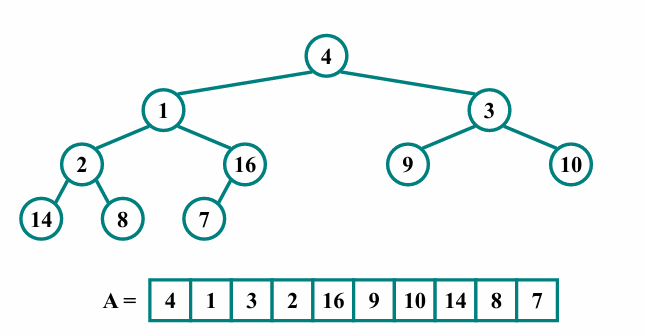
위와 같은 배열이 있습니다.
그림에서 leaf node들은 이미 max heap의 성질을 만족합니다.

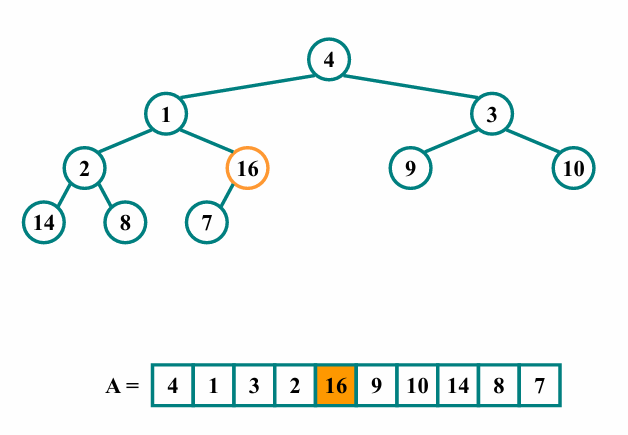
idx = 4 인 노드를 살펴봅시다.

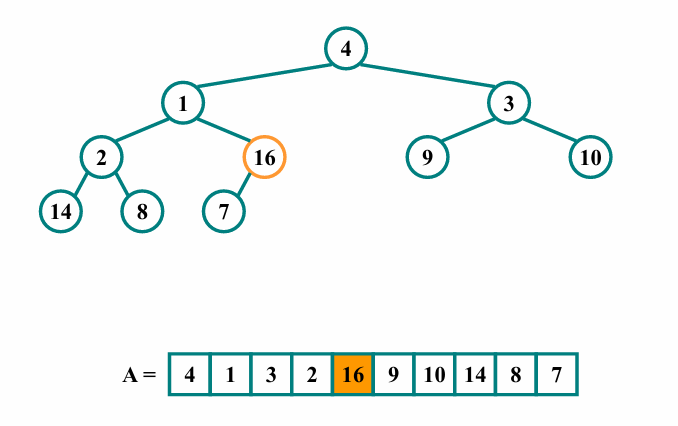
다음의 노드는 최대힙의 성질을 만족합니다.
i값을 하나줄여 idx=3인 노드를 살펴봅시다.

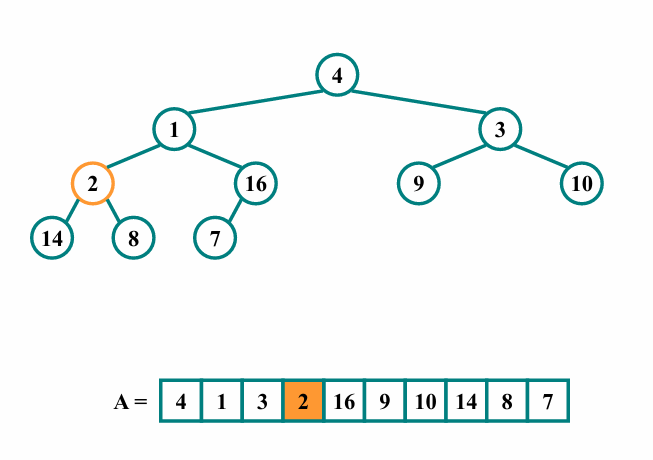
최대힙의 속성을 만족시키기 위해 heapify를 호출합니다.
그 결과 2를 root으로 하는 서브트리가 다음과 같이 만들어집니다.

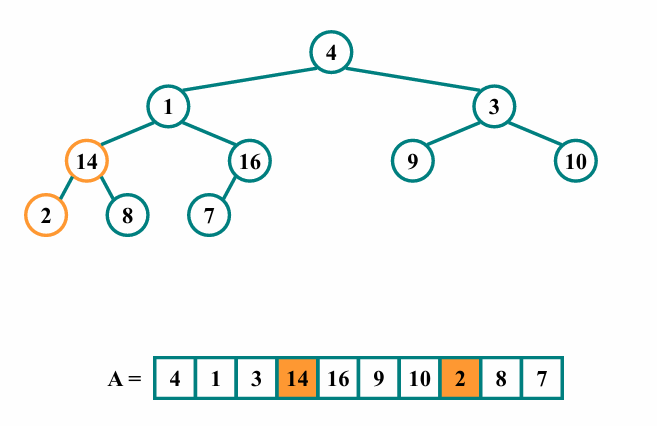
i값을 하나 줄여 idx=2인 노드를 살펴봅시다.
최대힙의 속성을 만족시키기 위해 heapify를 호출합니다.

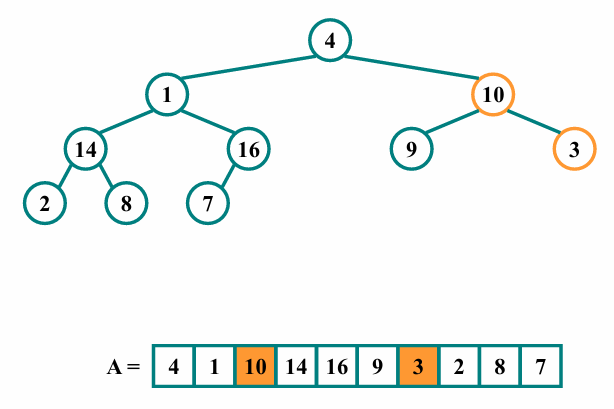
그 결과 i=2인 노드를 root으로 하는 서브트리는 최대힙의 속성을 만족합니다.
i를 하나 줄여 idx=1인 노드를 살펴봅시다.
최대힙의 속성을 만족시키기 위해 heapify를 호출합니다.



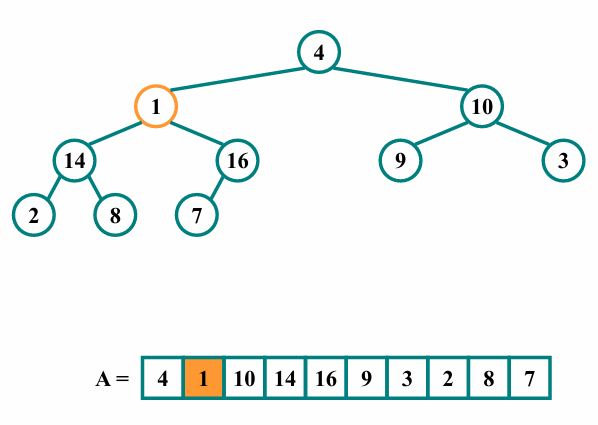
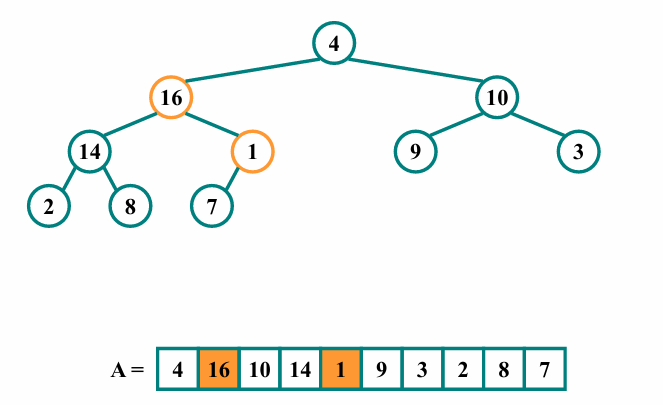
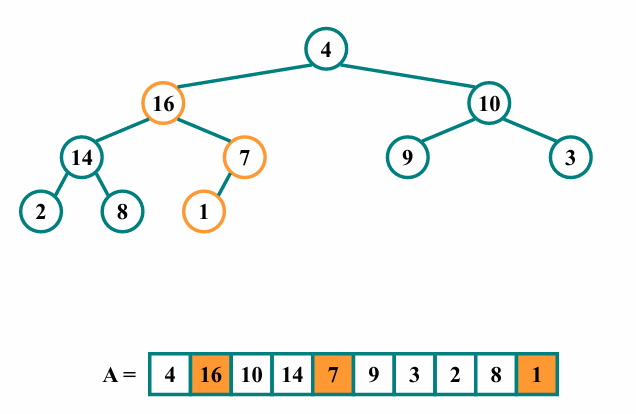
자식을 순회하며 float 하여 크기비교 후 위치를 재조정합니다.
마지막으로, i값을 하나 줄여 idx=0인 노드를 살펴봅시다.

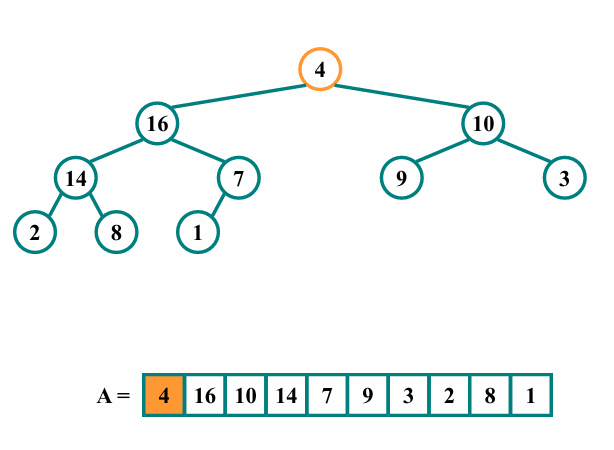
이 경우에도 마찬가지로 힙의 속성을 만족시키기 위해 heapify를 호출합니다.



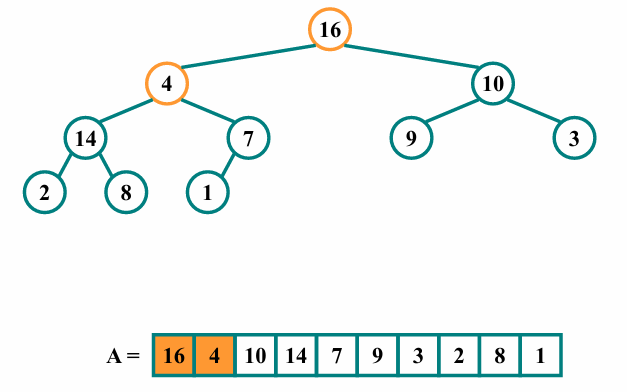
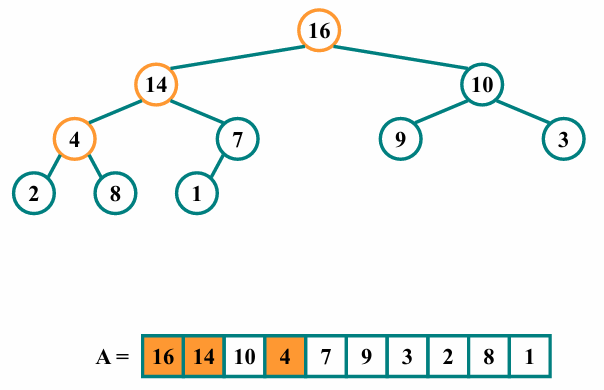
다음과 같이 자식을 순회하며 크기비교 후 위치를 재조정합니다.
루프가 종료되는 시점은 $i=0$ 이므로, 이 시점에서 불변식에 의해 모든 노드 $1,2,…,n$ 은 최대 힙의 루트가 됩니다.

Analysis of BuildHeap

대략적 점근적 상한 $O(n lg n)$

• 각각의 $Heapify()$ 함수호출은 $O(lg n)$ 의 시간복잡도를 가집니다.
• leaf node를 제외한 $⌊𝑛/2⌋$ 개의 node에서 heapify를 수행해야 하므로, $O(⌊𝑛/2⌋) = O(𝑛)$ 번의 heapify함수 호출이 있을 것 입니다.
• 따라서, 전체 시간복잡도는 $O(n lg n)$ 이 됩니다.

그러나 이는 대략적인 점근적 상한입니다. 그 이유는, $O(⌊𝑛/2⌋) = O(𝑛)$ 과정에서 생기는 오차때문입니다.

• 첫번째로, $⌊𝑛/2⌋$ 개의 모든 노드에서 HEAPIFY를 수행하는것이 아닙니다.
  추가 설명을 해보자면, 이진트리의 특성 상, $⌊𝑛/2⌋$의 노드는 트리의 하단부분에 위치하게 됩니다. 트리의 하단부 노드들은 깊이가 얕아서 Heapify 호출 시, 재귀깊이가 낮습니다. 즉 리프에 가까울수록 자식노드가 적기때문에 heapify호출이 더 빠르게 완료됩니다. 그러므로, 트리의 하단부에서 heapify를 호출하면, 상단부 노드에 비해 $O(log n)$보다 적은 시간이 걸립니다.

정확한 O(n) 분석

• 트리의 높이에 따라 레벨별로 노드의 수가 다르기 때문에, 이를 고려한 시간복잡도를 계산해봅시다.
• 트리의 레벨 h에 있는 노드들은 heapify를 호출할 때 최대h의 재귀깊이를 가집니다.
• 따라서, 특정레벨의 모든 노드들은 heapify 호출 시 최대 O(h)시간만큼 걸립니다.
• 각 높이에서 노드의 수는 $2^h$ 입니다.
• $2^h * O(h)$의 값을 0부터 n까지 더하면, 최종적으로 O(n) 시간 복잡도로 수렴합니다.