[algorithm] HeapSort Algorithm

HeapSort Algorithm

• HeapSort Algorithm은 배열을 정렬하는 알고리즘 중 하나입니다. 졍렬되지 않은 최대힙을 이용하여 정렬합니다.
  그 과정은 다음과 같습니다.

  1. $A[1…n]$ 의 주어진 배열을 $BUILD-HEAP(A, n)$ 함수를 호출하여 max Heap으로 변환합니다.
  2. 최대힙의 루트노드$A[1]$에 배열의 원소 중 최대값이 저장됩니다.
     해당 값을 배열의 마지막 위치 $A[n]$으로 옮깁니다.
  3. 힙에서 마지막 노드를 제거합니다.
  4. 이 경우, 오직, 루트노드와 자식노드의 위치만 바뀌었으므로, $A[1]$를 제외한 모든 노드들은 최대힙의 속성을 만족시킵니다.
  • 새로운 루트노드가 힙속성을 위반할 수 있으므로, heapify를 호출하여 최대힙을 복구합니다.
    5.마지막 요소는 이미 정렬됐으므로, 힙의 크기를 1 줄입니다.
    $n←n−1$
  6. n=2가 될 때까지, 위의 2~4 단계를 반복합니다.

HeapSort_ PesudoCode

HEAPSORT(A, n)
BUILD-HEAP(A, n)
for i ← n downto 2 do
    exchange A[1] ↔ A[i]
    HEAPIFY(A, 1, i - 1)
    

예시를 통해 알아봅시다.

• 다음과 같이 정렬되지 않은 배열 A가 존재합니다.

  

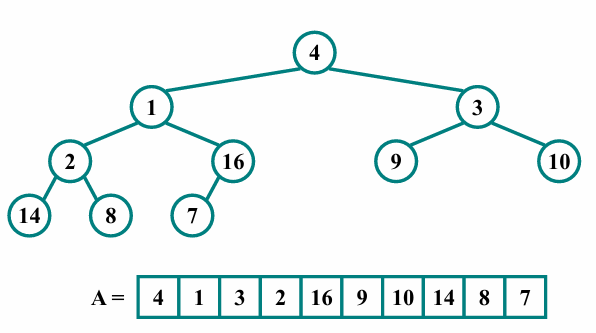
• $A[1…n]$ 의 주어진 배열을 $BUILD-HEAP(A, n)$ 함수를 호출하여 max Heap으로 변환합니다.

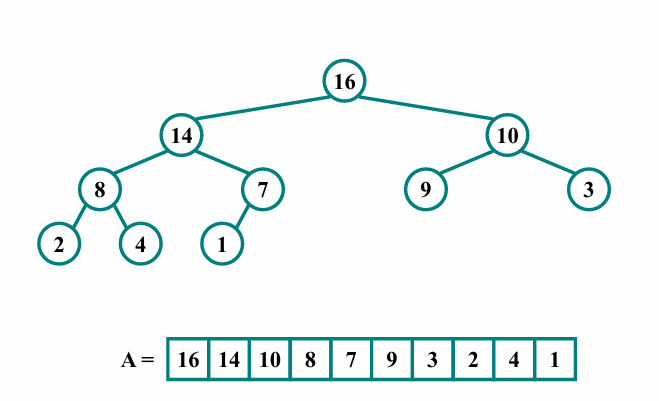
• 루트노드와 마지막 원소의 값을 교환합니다.
  
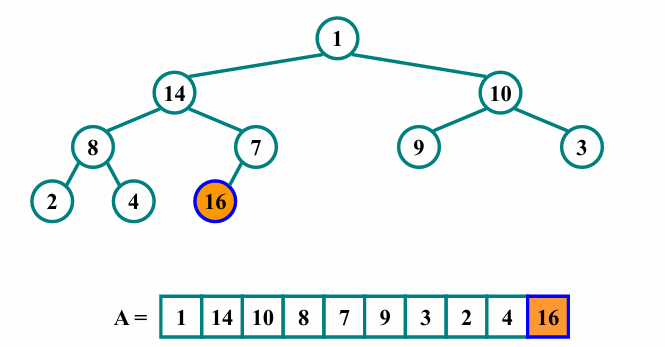
• 마지막노드는 leaf node이므로 정렬됐지만, 마지막 노드를 제외한 root노드를 트리로 하는 배열은 아래와 같이 최대힙의 속성을 위배합니다.
  
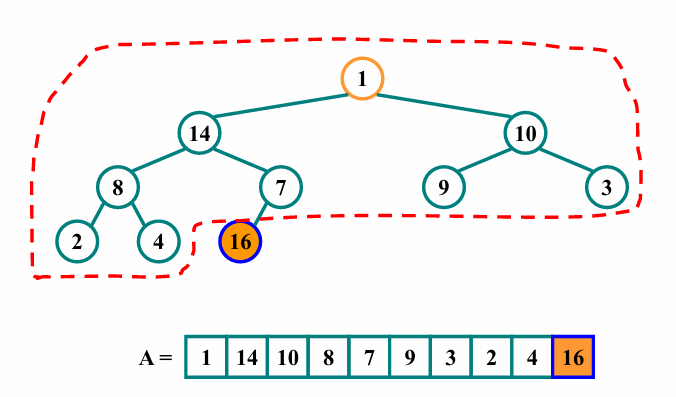
• 나머지 요소들을 정렬하기 위해, 마지막 노드를 제외한 나머지 원소에 대해 Heapify를 진행합니다.
  
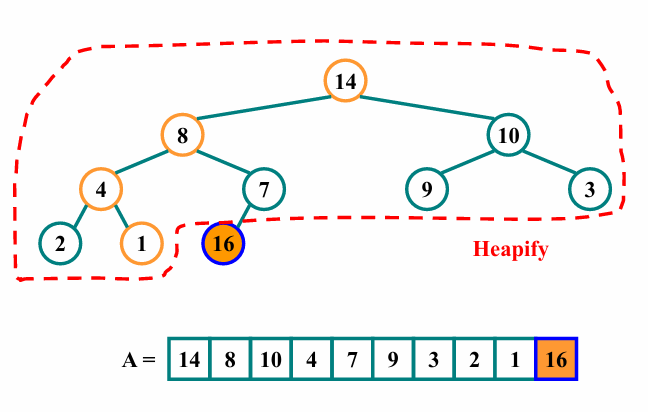
  그 다음 i를 1줄인 이후, 다음노드에 대해 아래와 같이 위의 과정을 반복합니다.
  
  
  
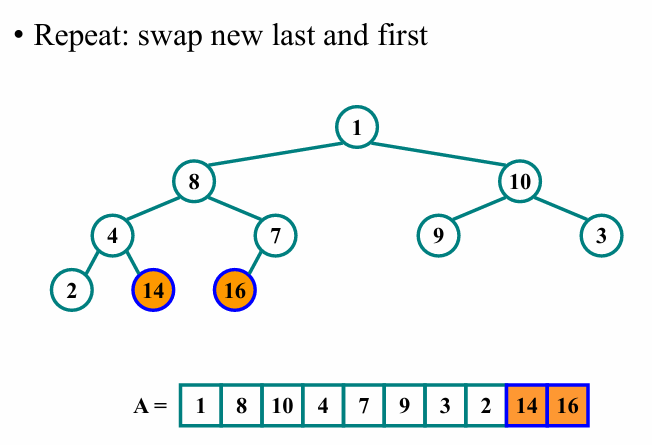
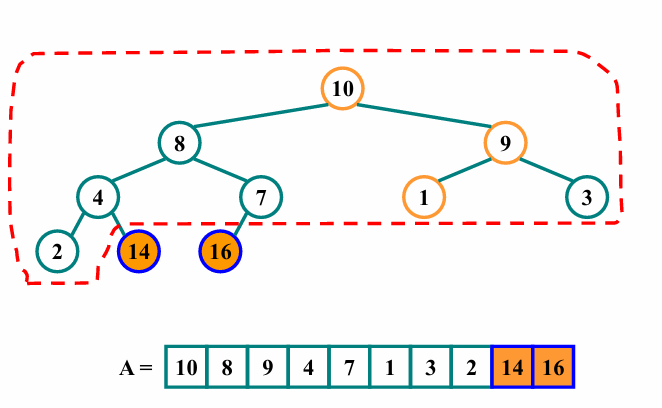
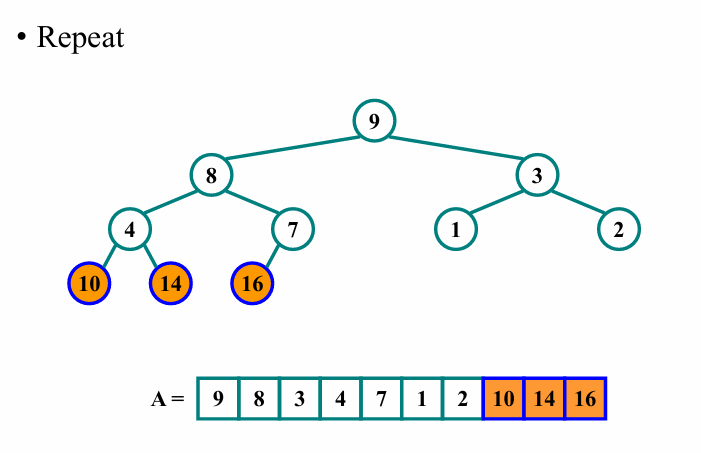
  이렇게 반복하다보면 최종적으로 아래와 같이 배열의 모든 요소가 크기순서대로 정렬된 것을 확인할 수 있습니다.
  

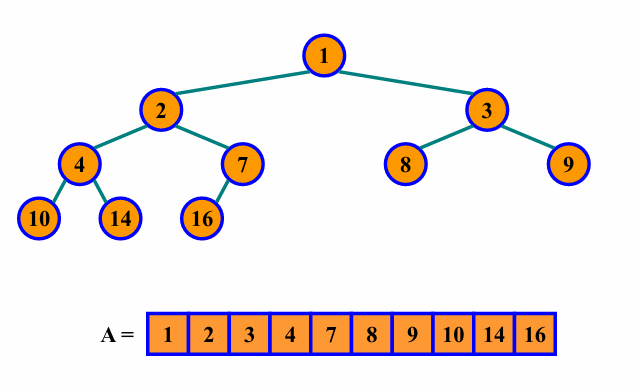
HeapSort Run Time Analysis

• $BuildHeap()$ 함수는 $O(n)$의 시간복잡도가 걸립니다.

• $Heapify()$함수는 n-1번 호출되므로, $O(log n)$의 시간복잡도가 수행됩니다.

• 따라서, $HeapSort()$함수의 총 시간복잡도는 다음과 같습니다.

  $O(n) + (n- 1) O(lg n)$
  $= O(n) + O(n lg n)$
  $= O(n lg n)$

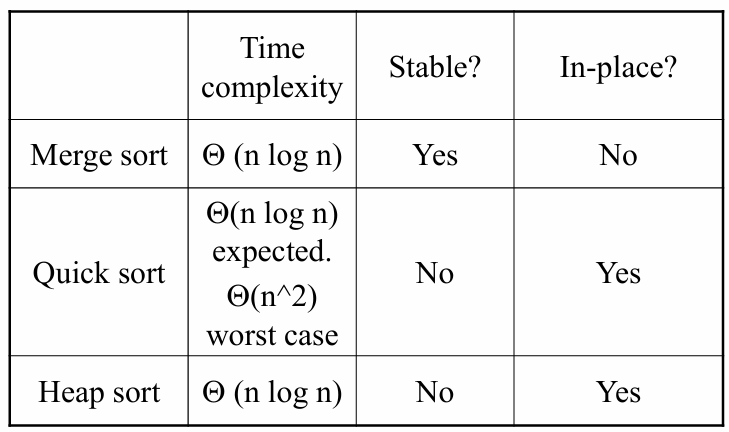
Time Complexity Comparsion