본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1
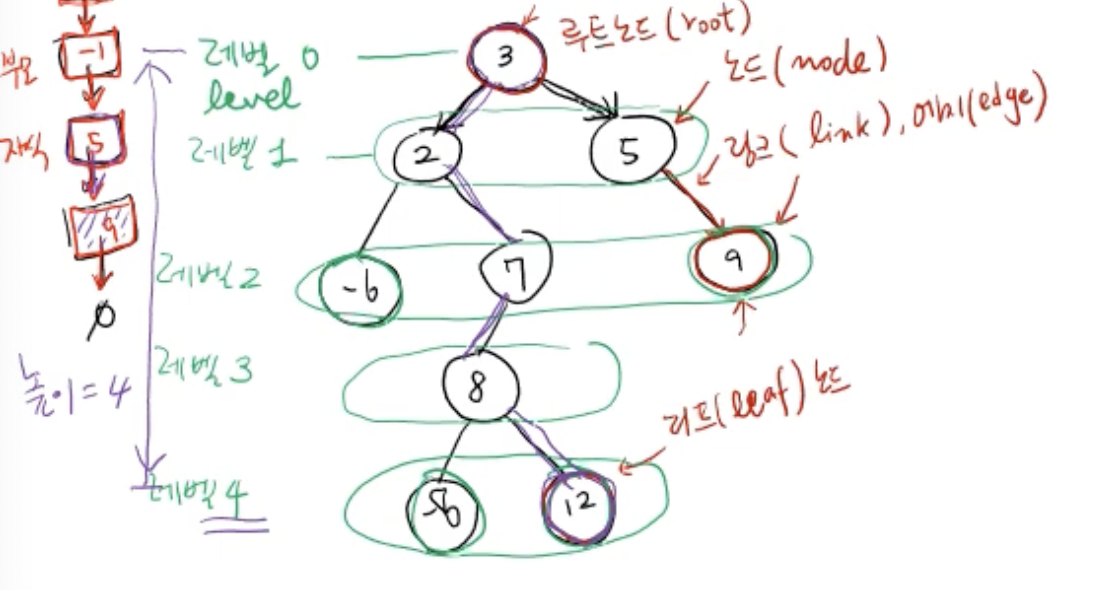
- 순차적 자료구조: 순서에 따라 저장되어 있고, 인덱스를 알면 그 위치에 저장된 값을 알 수 있다
- 배열: 인덱스 i=0, 1, ...
- 연결리스트: 링크 (next, prev)를 따라 다음 노드에 저장된 값 알 수 있음 (저장되어있는 순서가 있는 거지)
- 연결리스트를 head node를 맨 위에, tail 노드를 가장 아래에 위치시키면, root-부모-자식(부모)-자식.. 의 관계로 정의 ➡️ Tree
- 연결리스트는 자식 노드가 없거나 최대 1개인 Tree의 특별한 케이스라고 볼 수 있음
트리 (Tree)
-
일반적인 트리 구조는 여러 개의 자식 노드를 가질 수 있다
-
이진 트리 (Binary Tree): 자식 노드가 최대 2개, 가장 많이 쓰이는 트리, 3개 이상은 안돼
-
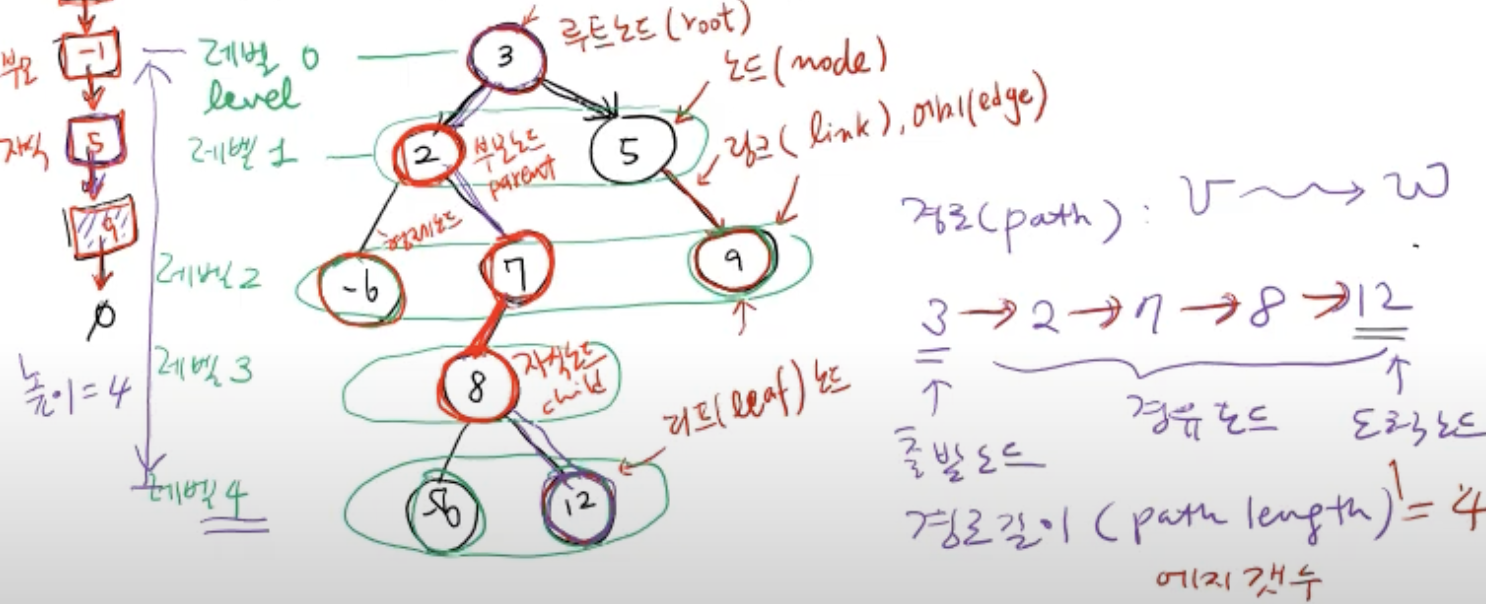
루트노드(root), 노드(node), 링크(link, edge)
-
자식이 없는 노드: 리프 (leaf) 노드
-
자식노드(child), 부모노드(parent), 형제노드
-
레벨(루트 노드 0부터~), 높이 (트리의 높이 = 레벨)
-
경로(path): 노드 v -> 노드 w
-
경로 길이(path length): 출발 노드에서 목적지 노드까지의 길이 = edge 개수
-
트리의 Code 구현
-
표현법 1 : 리스트, level 0부터 차례대로 level 1,.., level n까지
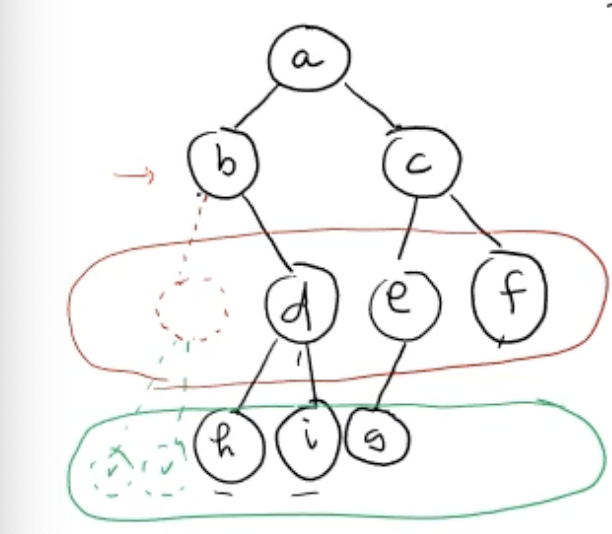
- 이때 왼쪽 -> 오른쪽 순서, 비어 있는 노드는 NaN 등으로 비워둠
- A = [a, b, c, Nan, d, e, f, Nan, Nan, h, i, g]
-
표현법 2: 재귀적 리스트
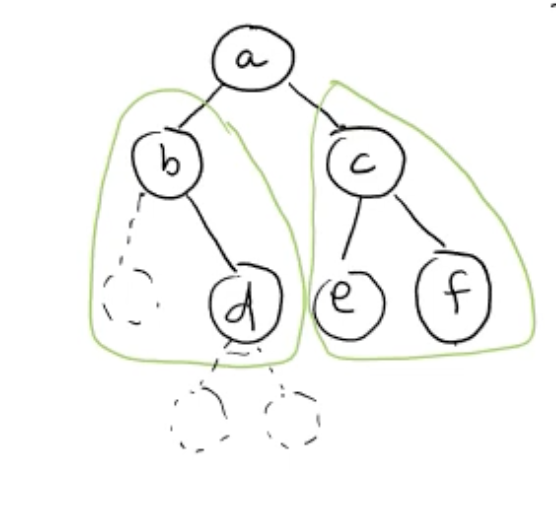
- [a, [a의 왼쪽 subtree], [a의 오른쪽 subtree]]
- [a의 왼쪽 subtree] = [b, [], [d, [], []]]
- [a의 오른쪽 subtree] = [c, [e, [], []], [f, [], []]]
-
표현법 3: 노드 class 정의
- key, child 2개의 link(left, right), 부모 노드를 가리킬 parent link의 총 4개 요소 필요
