7. 힙(Heap)

Yeonghyeon·2022년 9월 20일

자료구조 및 알고리즘

목록 보기

7/12

본 포스팅은 아래의 출처를 참고하여 정리한 것입니다.
https://www.youtube.com/watch?v=PIidtIBCjEg&list=PLsMufJgu5933ZkBCHS7bQTx0bncjwi4PK&index=1

힙(Heap):

힙 성질(heap property) 만족하는 이진트리
- 이진트리: 자식 노드를 최대 2개까지 가질 수 있는 트리
- 리스트로 표현하는 이진트리
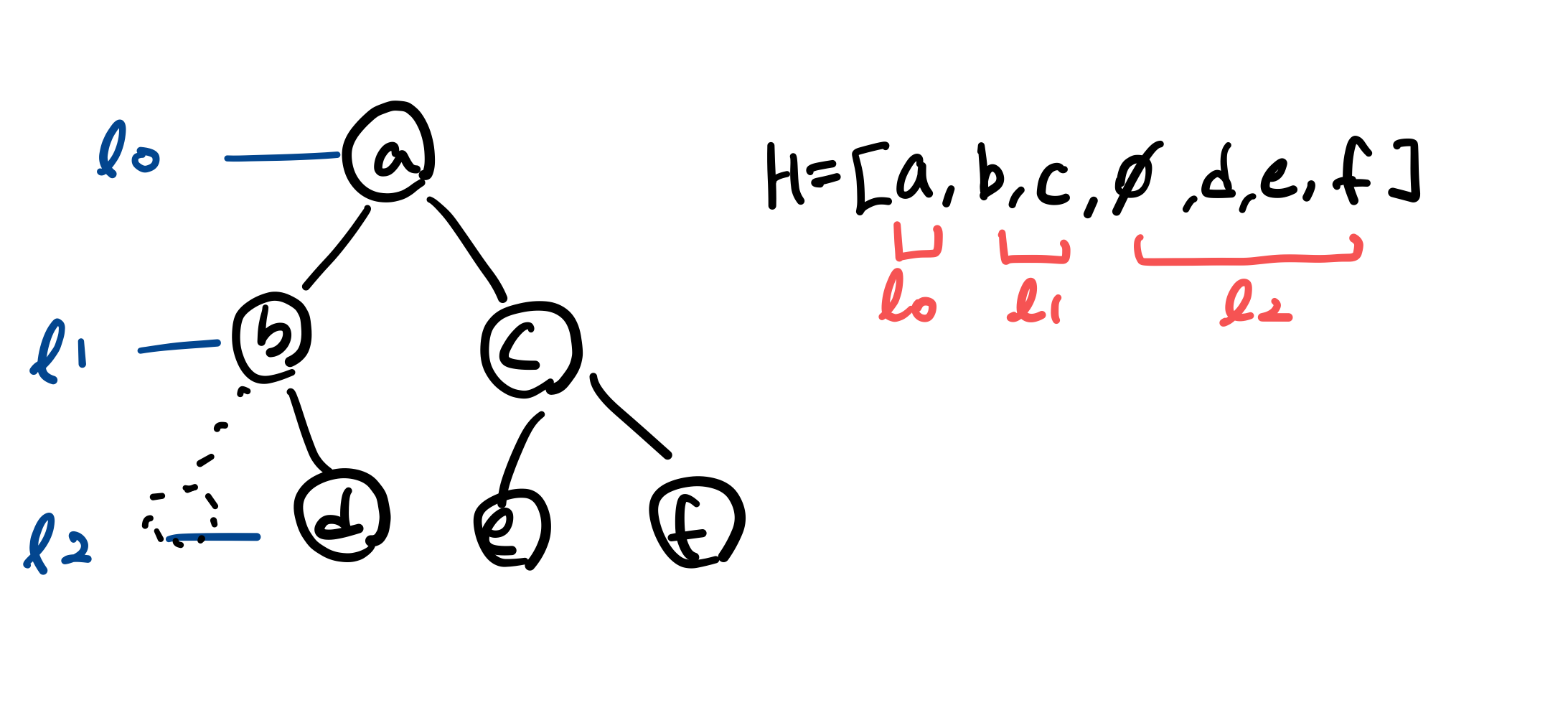
  - 장점이 무엇일까
    - H[0]의 왼쪽 자식 노드=H[1], 오른쪽 자식 노드=H[2]
    - H[2]의 왼쪽 자식 노드=H[2*2+1]=H[5]=e, 오른쪽 자식 노드=H[2*2+2]=H[6]=f
      - 각 레벨마다 그 레벨의 자식노드는 다음 레벨에 있는데, 각 레벨마다 모두 차있다고 처리(비어있으면 공집합으로 표기)하기때문에 각 레벨에 있는 모든 노드들이 리스트에 자리를 차지함, 즉 각 노드마다 자식노드 2개의 자리를 리스트에 차지한다. ➡️ 매 레벨마다 2배씩 자리를 차지
    - 일반화: H[k]의 왼쪽 자식노드=H[k*2+1], 오른쪽 자식노드=H[k*2+2]
    - 반대로 H[k]의 부모노드=H[(k-2)//2]
    - 장점: 상수 시간 $O(1)$ 의 연산으로 자식노드와 부모노드의 키값을 알 수 있다!
    - 단점: 비어있는 자리에 대한 불필요한 메모리 공간 낭비
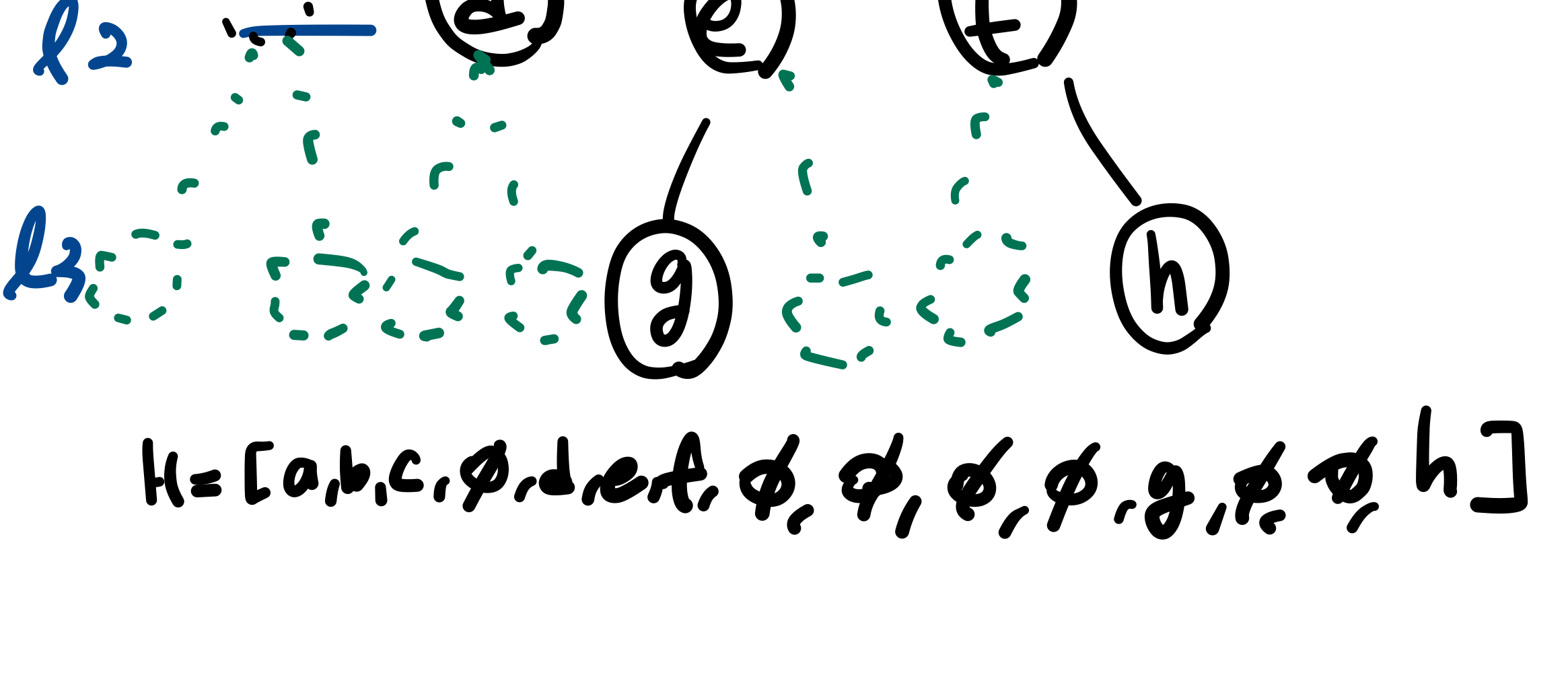
    - 자리를 낭비하지 않으려면 레벨마다 꽉꽉 차있는 형태의 예쁜 모양(마지막 레벨 제외) ➡️ Heap(힙)

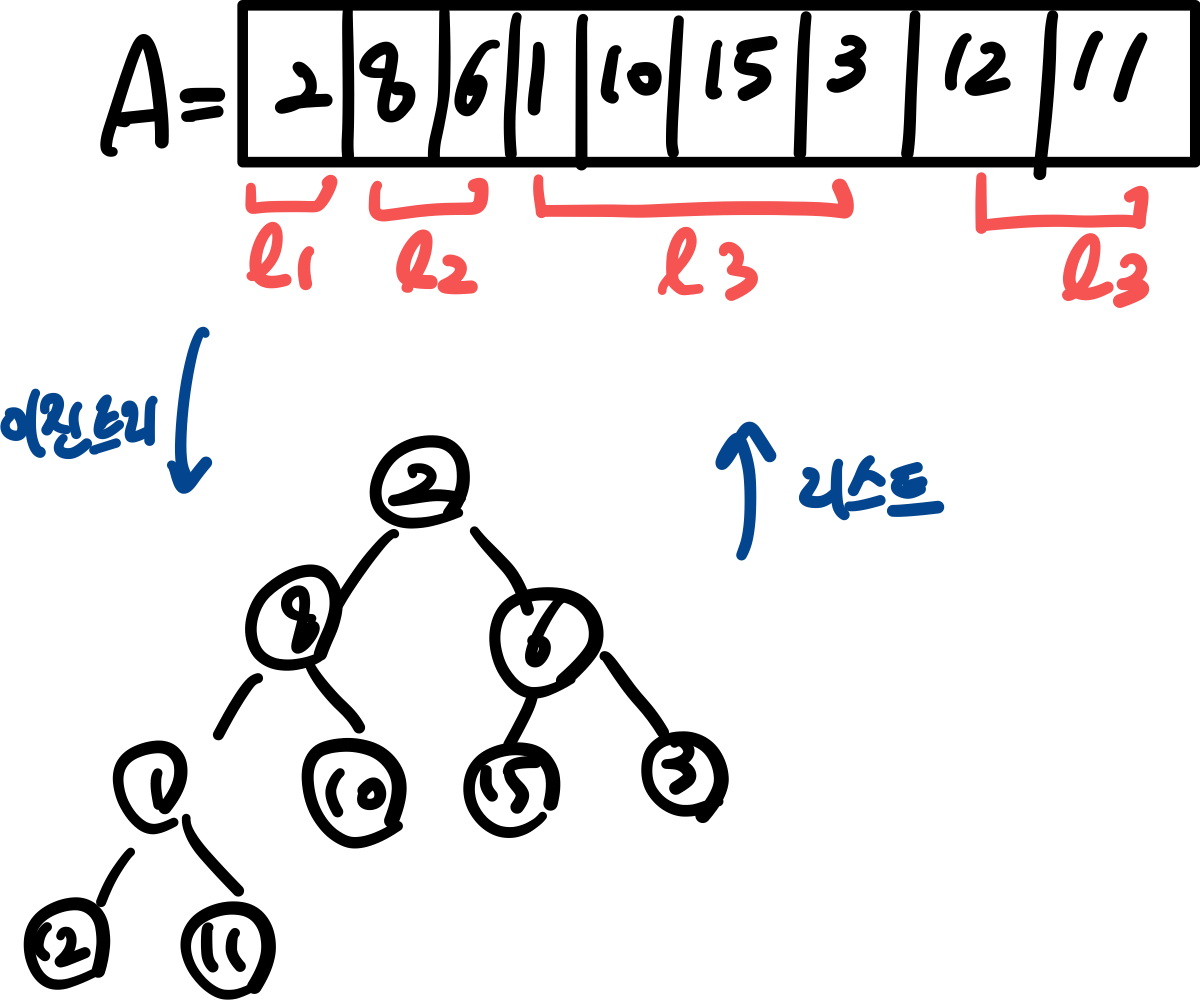
🌟 힙 성질

모든 부모노드의 key 값은 자식 노드의 key 값보다 작지 않다
위 예시 트리에서는 힙 성질을 만족하지 않음
즉, 다음을 만족하는 이진트리를 Heap이라고 부름
1. 모양 성질: 모든 레벨에 노드가 꽉 차있고 마지막 레벨만 왼쪽부터 채워져있는 형태
2. 힙 성질: 힙 성질 만족하지 않으면 자리를 바꿔 만족하도록 변경함

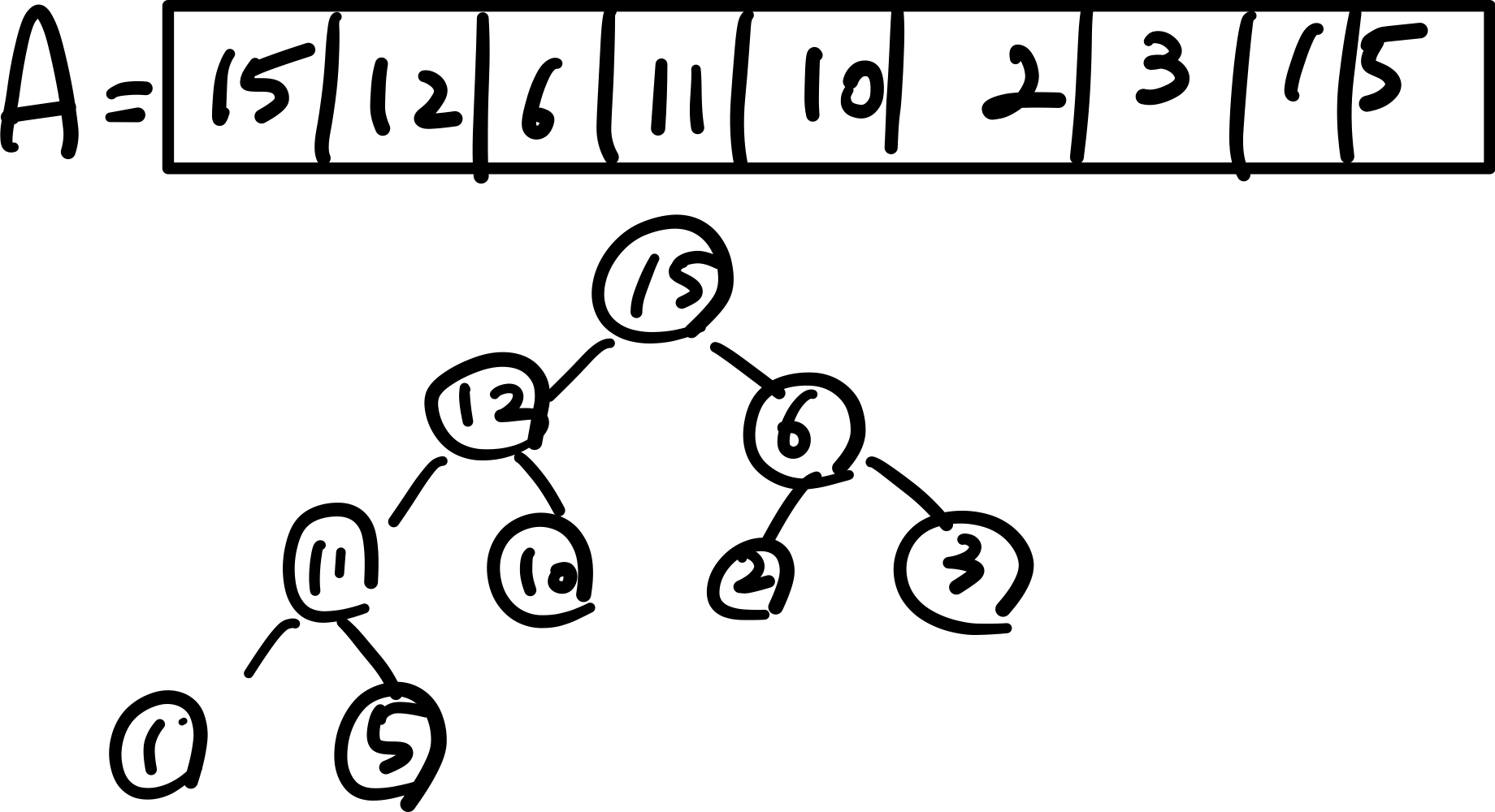
다음 예제 트리는 힙 성질을 만족함 ➡️ 힙
힙의 루트 노드: 가장 큰 값
힙의 제공 연산
- insert: 삽입 (힙 성질 만족하도록) ➡️ $O(logn)$
- find_max: return A[0] (루트노드) ➡️ $O(1)$
- delete_max: maximum을 삭제 ➡️ $O(logn)$
  - 지우고 남은 n-1 개의 노드들도 힙을 유지해야 됨
- 이때 모든 연산은 초기에 make_heap이 필요함: 주어진 값들을 힙 성질에 맞게 재배치하는 작업

make_heap 연산

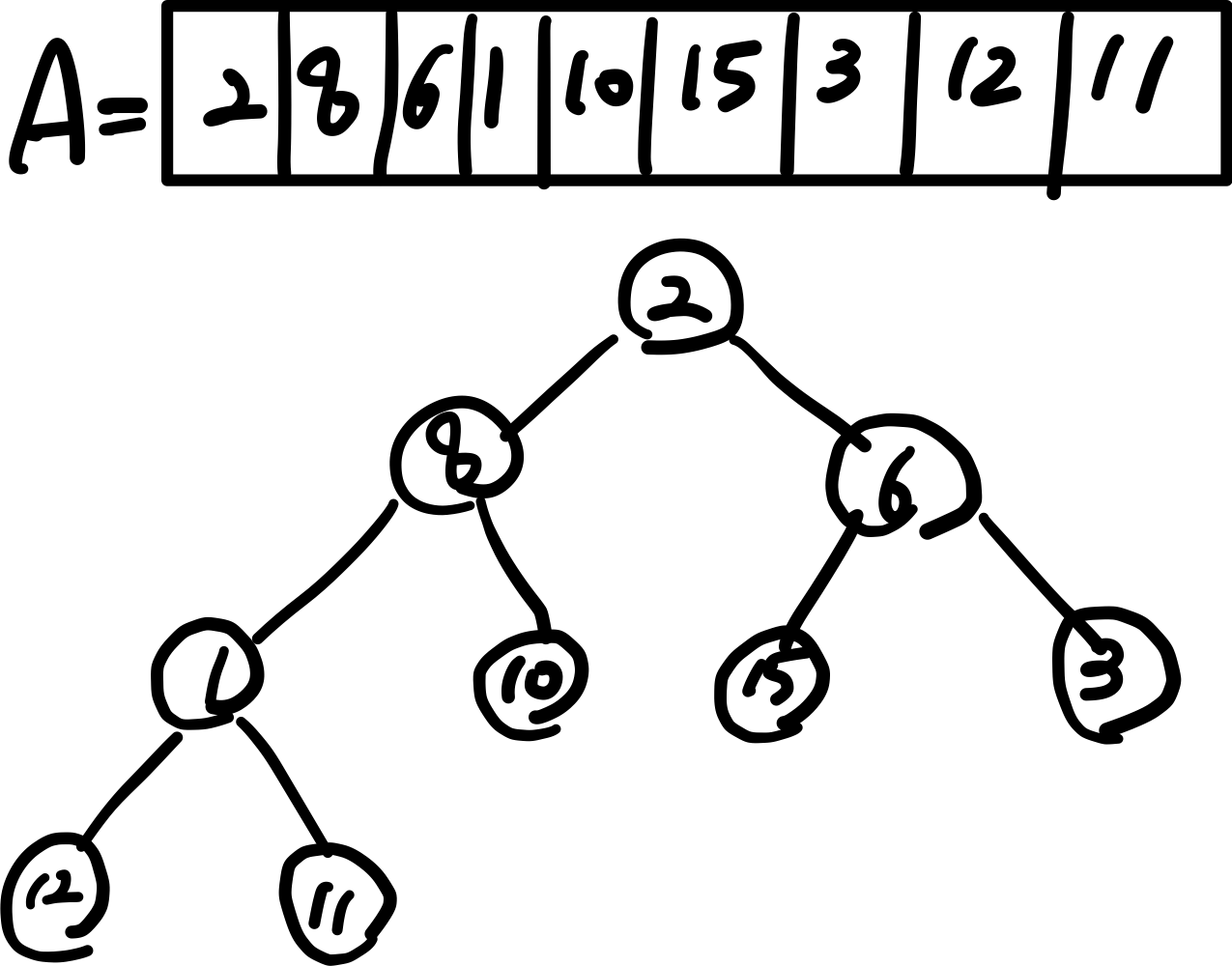
힙 성질을 만족하지 않은 트리를 자리 재배치하여 만족하도록 변경
make_heap: heapify_down 연산을 반복
- 가장 마지막 원소부터 루트까지 차례대로 살펴보면서 밑으로 내려가면서 자리를 찾아가는 것
- ex) 11,12,3,15,10은 리프노드로 자식노드가 없기때문에 그자체로 힙 성질 만족
- 그 다음 1은 1의 왼쪽 자식, 오른쪽 자식을 살펴봄 ➡️ 상수 시간의 키값을 읽는 장점 활용! ➡️ H[k*2+1], H[k*2+2]
  - A[3], A[3*2+1], A[3*2+2]: 자식 노드가 부모 노드보다 키 값이 크므로 키 값을 교체함 ➡️ 둘 중 더 큰 값으로 교체

즉, heapify_down은 어떤 노드에서 그 노드의 자식 노드 방향으로 내려가면서 힙 성질을 만족하도록 자리를 재배치

수도 코드

def make_heap(A):
	n = len(A):
    for k in range(n-1, -1, -1):
    	# A[k] -> heap 성질 만족하도록 내려보내
        heapify_down(k, n) # A의 k 위치를 밑으로 내려보내고, n은 힙의 원소 개수

def heapify_down(k, n):
	# A{k], n 값
    while A[k] != leaf_node:
    	L, R = 2*k+1, 2*k+2
        m = max_index(A[k], A[L], A[R])
        if k != m: # 부모노드 키 값 < 자식노드 키 값
        	A[k] <-> A[m]
            k = m
        else: # 힙 성질 만족
        	break

heapify_down을 k에 대해 n번 호출 ➡️ heapify_down의 시간을 t라 할 때 $O(n*t)$ 의 시간
- heapify_down: 최악의 경우 k 번째 원소가 리프노드까지 도달할 수 있음 ➡️ 가장 오랜 시간이 걸리는 경우는 루트노드에서 가장 밑의 레벨까지 도달하는 경우 ➡️ while문 안에서 max_index 찾고 키 값 변경하는 것은 $O(1)$ ➡️ 최악의 경우 힙의 높이(h) 만큼 내려갈 수 있으므로 $O(1*h) = O(h)$
- 따라서 $O(n*t)$ = $O(n*h)$
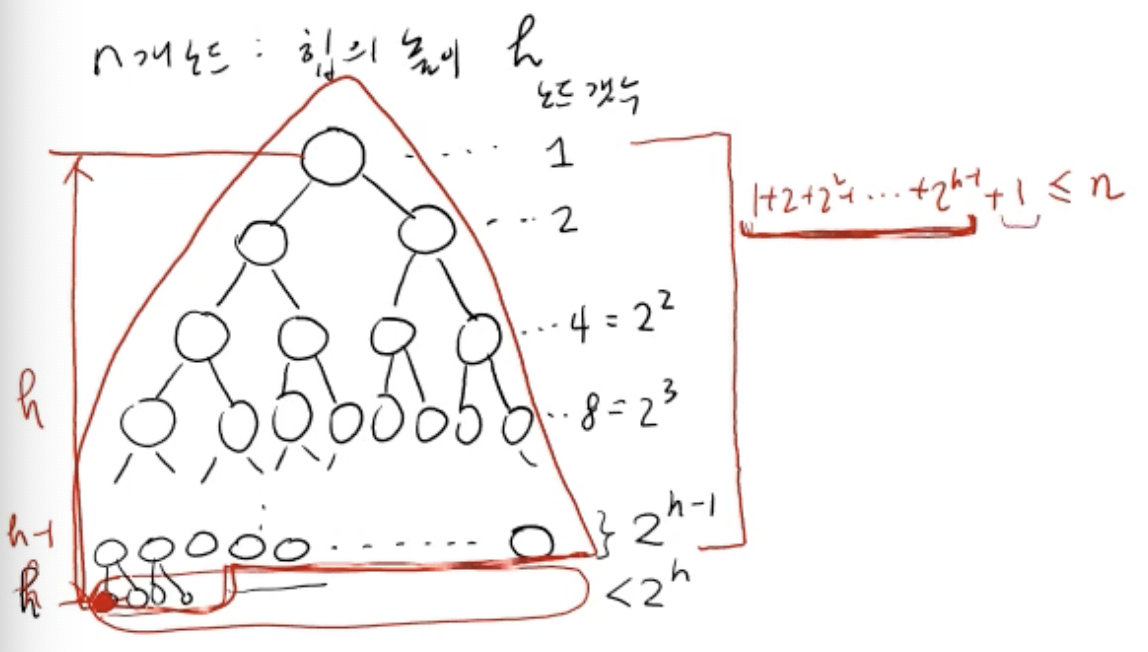
- n개의 노드를 가진 힙의 높이 h는 각 레벨마다 1, 2, 4, 8, ... $2^h$ 노드가 존재
  - 마지막 h 레벨의 노드는 꽉 차있지 않을 수도 있으니 $< 2^h$ 이다.
  - $1+2+2^2+...+2^{h-1}+1 \le n$ (맨 마지막 h 레벨의 노드는 최소 1개 있다고 가정하면)
  - $= \frac{2^h-1}{2-1}+1=2^h \le n$
  - $= h \le log_2^n$ (양변에 log 취함)
  - ➡️ 즉, n개의 노드를 가진 heap의 높이 h는 아무리 커봤자 logn을 넘지 않는다
heapify_down: $O(h)=O(logn)$
make_heap: $O(nh)=O(nlogn)$
근데 사실 루트노드가 아닌 다른 레벨에 있는 노드에서 heapify_down하면 시간이 덜 걸리지 ➡️ 어떤 레벨에 있냐에 따라 heapify_down은 실제로 $O(n)$ 까지 가능

Insert와 delete_max 연산

insert

insert(14): A.append(14): 맨 마지막에 키 값 집어넣고 heapify_up 실행
14가 들어옴으로써 힙 성질 만족하지 않으므로 자리 재배치 필요
- 14를 위로 올려보내면서 자기 자리 찾도록 ➡️ 자신의 부모노드의 값이랑 비교
- 부모노드보다 자신의 키 값이 더 크므로 자리를 교체
- A.heapify_up(k): A[k]를 루트노드 방향으로 이동하면서 힙 성질을 만족하도록 heapify 하는 것

수도코드

def heapify(k): # A[k]를 heapify
	while k > 0 and A[(k-1)//2] < A[k]: # root 노드 인덱스에 도달하지 않았고, 부모노드의 키 값이 자식노드의 키 값보다 작으면
		A[k], A[(k-1)//2] = A[(k-1)//2], A[k]
        k = (k-1) // 2

heapify 함수가 $O(logn)$ 시간이 걸리므로 insert도 $O(logn)$ 시간

find_max:

가장 큰 값이 루트노드에 저장됨
return A[0]
- 힙의 변경 없이 그냥 값만 리턴해주면 됨
$O(1)$

delete_max:

루트노드를 삭제 후 루트노드에 어떤 값으로 다시 채워야 됨 ➡️ 힙 성질 유지하도록
맨 마지막 레벨의 마지막 노드가 루트노드로 들어가면서 다시 heapify
루트노드에서 내려가면서 힙 성질 유지하도록 자식노드와 자리 swap ➡️ heapify_down
heapify_down(0, n)

수도코드

def delete_max:
	if len(A) == 0: # 비어있는 트리
    	return None
    key = A[0]
    A[0], A[len(A)-1] = A[len(A)-1], A[0] # 가장 마지막 리프노드와 swap
    A.pop() # 리스트의 가장 마지막 원소 제거
    heapify_down(0, len(A))
    return key

$O(logn)$

연산 비교

make_heap: $O(n), O(nlogn)$
insert: $O(logn)$
find_max: $O(1)$
delete_max: $O(logn)$
heapify_down: $O(h)=O(logn)$
heapify_up: $O(h)=O(logn)$
주의할 점은 search 함수가 없음!
- 배열, 리스트, 연결리스트, 해시테이블과 다르게 일일이 하나씩 다 비교하는 방법말고 새롭게 빠르게 찾을 수 있는 방법이 없기 때문
즉, 힙은 search를 효율적으로 할 수 있는 자료구조는 아니고, insert, find_max, delete_max를 $O(1), O(logn)$ 시간 내에 할 수 있는 특화된 자료구조
- 서치를 많이 하기보단, insert해서 가장 큰 값을 찾거나 가장 큰 값을 지우는 연산이 많이 필요한 어플리케이션에 힙을 쓰자
find_min과 delete_min이 필요할 시 그것을 만족하는 힙을 만들면 됨
- 우리가 방금 만든 힙은 max-heap이라고 함
- min-heap: 부모노드는 자식노드보다 항상 값이 작도록 만족하는 힙
- 부등호 방향을 반대로 해주면 똑같이 만들 수 있음
또한 힙 정렬 heap_sort()도 가능
- n개의 숫자를 입력으로 받고 make_heap으로 힙 구성: $O(nlogn)$
- n 번을 반복하면서 delete_max를 호출하면 됨
  - 근데 값이 지워지므로 A.pop() 하지말고 그대로 놔두고 다시 heapify해서 적당한 자리로 배치해줌