본 포스팅은 Fastcampus 강의를 수강하며 일부 내용을 정리한 글임을 밝힙니다. 보다 자세한 내용은 아래 강의를 통해 확인해주세요.
참고 : Fastcampus 딥러닝을 활용한 추천시스템 구현 올인원 패키지 Online

---

Ch 06. Model-based Collaborative Filtering

---

Latent Factor Model

- Latent: 잠재된

- Factor: 요소, 특징

➡️ 잠재된 특징들을 가지고 온 모델(기존의 데이터에서 잠재 의미를 가져온다)

• 사용자/아이템 특성을 벡터로 간략화(요약)하는 모델링
• 사용자/아이템 특성 간 복잡한 관계 학습
  • 기존에는 복잡/심플 신경 안썼는데, 모델한테 스스로 잠재적 요인 찾아서 간략화하는 작업이 이 모델의 특징
• 사용자/아이템 행렬에서 사용자와 아이템을 factor로 나타내는 방법
• 사용자와 아이템이 같은 벡터 공간에 표현 ➡️ 같은 공간에서 어떤 사용자와 어떤 아이템이 비슷하구나 체크 가능
• 사용자와 아이템을 모르는 차원에 표현 (몇 개의 차원인지 모름)
• 같은 벡터 공간에서 사용자와 아이템이 가까우면 유사, 멀리 떨어져 있으면 유사 X
  • latent factor들로 모델이 학습한 것을 바탕으로 이들이 유사한지 판단 가능

Singular Value Decomposition(SVD)

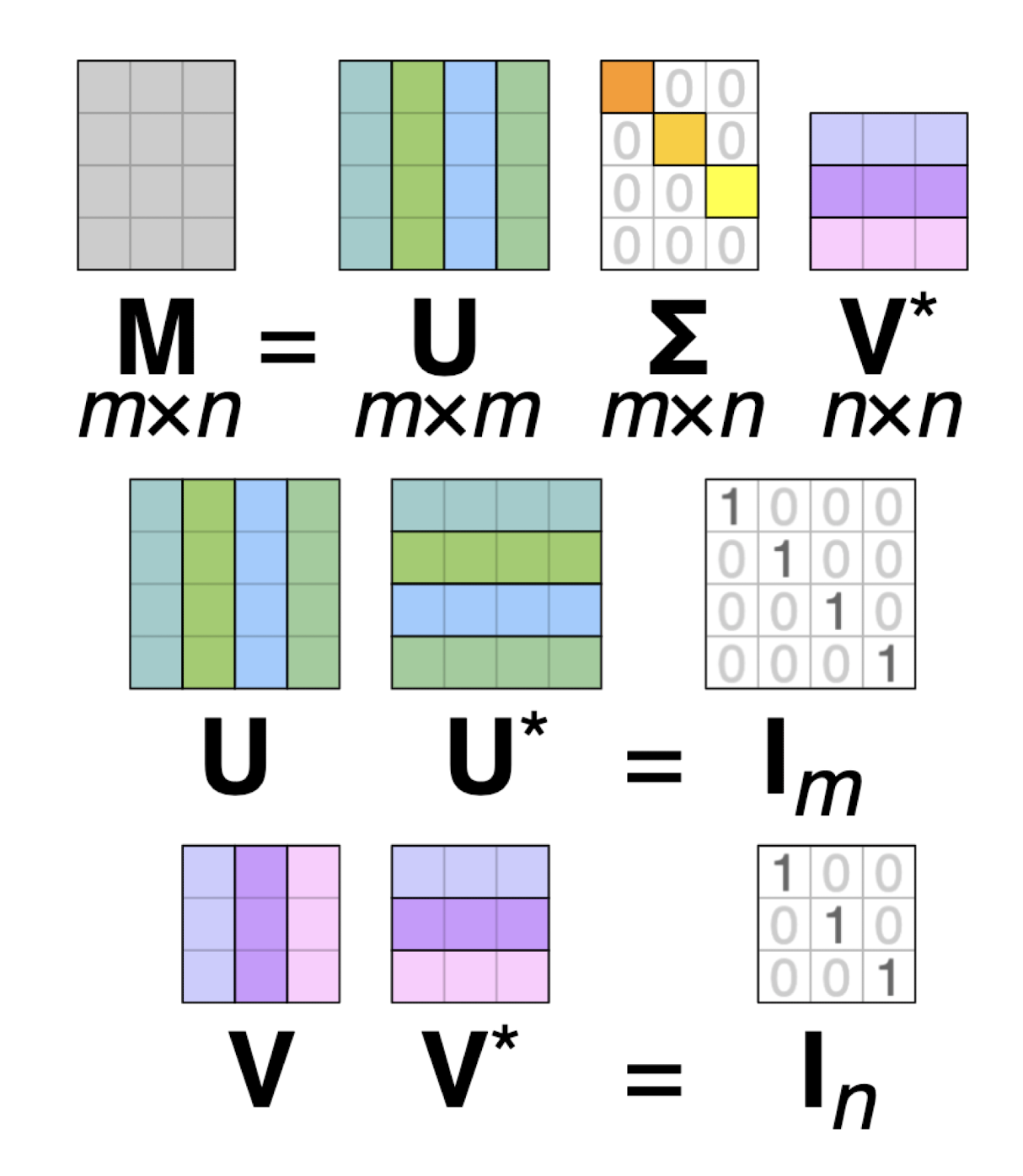
우리가 가진 행렬(user-item rating matrix)을 분해 ➡️ 분해함으로써 얻을 수 있는 벡터값들이 Latent Factor

$A=UΣV^T$

• $U$: 고유값 분해로 얻은 mxm 직교 행렬
  • $AA^T=U(ΣΣ^T)U^T$
  • $U$의 역벨터: $A$의 left singular vector
• $V$: 고유값 분해로 얻은 nxn 직교 행렬
  • $A^A=V(Σ^TΣ)V^T$
  • $V$의 열벡터: $A$의 right singular vector
• $Σ$: mxn 대각 행렬
  • 고유값 분해해서 나온 eigenvalue(고윳값)의 제곱근의 대각 원소
  • 대각 원소 = $A$의 특이값

• 차원 축소 기법 중 하나

  • 참고: PCA(Principal Component Analysis)

• 사용자와 아이템 간 데이터를 행렬 R로 나타냄

• 형렬 U: 사용자와 latent factor

• 행렬 V: 아이템과 latent factor

  • 행렬 U는 사용자에 대한 특징, 행렬 V는 아이템의 특징
  • 두 행렬이 Latent Factor라는 것으로 인해 함께 만날 수 있는 것!
  • 결국 추천시스템에서의 SVD 해석은 Latent Factor는 행렬 U와 V의 관계를 나타내는 factor라고 생각해볼 수 있다!

• 행렬 U와 V의 모든 열벡터는 특이벡터(singular vector) ➡️ 모든 특이벡터는 서로 직교
  $U^TU=I,V^V=I$

• 행렬 Σ의 대각성분은 M의 특이값

• 사용자와 아이템의 관계를 2차원 직교좌표계로 표현

  • 사용자와 아이템의 고유값 계산 ➡️ 고유값으로 기존 평점 데이터 다시 계산

• Latent Factor들을 좋은 값으로 갖고있어야 원본 행렬에 최소의 근사치로 복원 가능

SVD 적용 이유

• 데이터 차원 축소
  • 노이즈 제거, Sparse matrix 형태로 큰 데이터 축소 (많이 sparse한 데이터들을 더 작은 공간으로 매핑하게끔)
• 행렬 U: user와 latent factor 간의 관계
• 행렬 V: item과 latent factor 간의 관계
• 행렬 Σ: 대각행렬, latent factor의 중요도
• Latent factor: user와 item이 공통으로 갖는 특징
• 단, latent factor의 뜻을 이해하기 어렵기 때문에 추천에 대한 구체적 설명이 어려움

Matrix Factorization

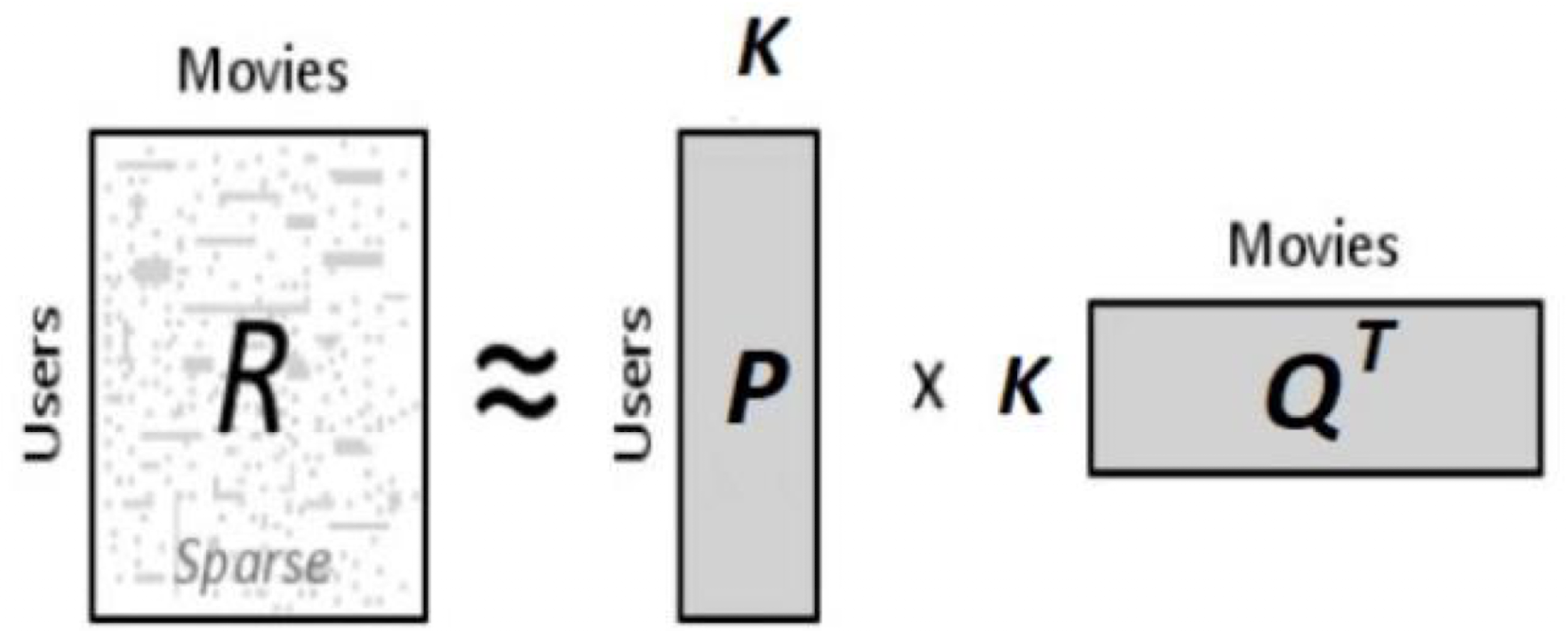
• Latent Factor Model을 구현하는 방법
• Rating Matrix를 분해하는 과정임
  • ex) SVD를 통해 matrix factorization 가능 (추후 실습)
• $|U|\times|I|$: user-item rating matrix ($rank$ $k < n$)
  • $k$: 우리가 지정하는 숫자
• $P→|U|\times k$: matrix of user factors
• $Q→|I|\times k$: matrix of item factors

➡️ 최종적으로 sparse한 matrix $R$을 k값의 조정에 따라 $P$와 $Q$로 근사해나가는 과정(예측(e.g. 평점))
➡️ 달리 말해 매트릭스의 비어있는 부분의 값을 예측하는 문제로 바꿔서 생각

그림으로 다시 이해

• 분해한 행렬 $X$와 $Y$를 곱하여 평점을 예측
• 임의의 차원 수 f는 직접 정함
• $r_{ui}$(예측된 rating)$=X^T_u\times y_i$
• $R$(원래 rating matrix)과 $R^;$(예측 matrix)이 서로 유사하도록 학습하는 과정
  • 관측된 data만 사용

More on Matrix Factorization

• Matrix Completion 문제
  • 비어있는 matrix를 완성시키는 문제
  • 즉, 이러한 문제 풀기 위해 SVD(행렬분해)를 통해 행렬의 특이값들을 뽑아내고 특이값들을 바탕으로 user-latent factor 혹은 item-latent factor의 관계를 나타냄
• Other SVD
  • SVD++, thin SVD, compact SVD, truncated SVD, etc..
• Loss Function
  • Latent factor(feature) 학습
• Optimization
  • (Stochastic) Gradient Descent(SGD), Alternating Least Squares(ALS)

---

Recap

• Matrix Factorization은 Matrix Completion 문제
• Matrix Completion 문제 풀기 위해선, 결론적으로 user-item matrix를 분해해서 user와 item을 k라는 latent factor의 관계로 표현
• 표현된 k라는 latent factor들을 얼마나 잘 만드느냐에 따라 원래 가지고 있던 original rating과 예측 rating의 차이가 줄어든다(loss)
• 이 loss를 줄이는 과정이 latent factor를 학습하는 과정
• 학습을 최적화하기 위해 SGD, ALS 등이 필요하다

---

이후 강의에서 SGD, ALS를 바탕으로 matrix factorization이 어떻게 학습하고 최적화하는지 좀 더 살펴보자