Variational AutoEncoders

아래 사이트에서 일부를 정리한 글입니다.
https://www.jeremyjordan.me/variational-autoencoders/

AutoEncoder

• input data는 각 차원이 데이터에 대한 학습된 속성을 나타내는 encoding vector로 변환된다
• 이때 encoder network는 각 encoding 차원에 대해 single value를 출력한다
• 그후 decoder network가 이 single value들을 가져와 original input을 재생성하려고 한다
  

A variational autoencoder (VAE)

• latent space에서 observation을 설명하기 위한 확률론적 방법을 제공한다
• 각각의 latent state 속성을 설명하기 위해 single value를 출력하는 encoder를 만들기보단, 각 latent 속성에 대한 확률분포를 설명하는 encoder를 만든다

---

Intuition

• 예시로, 6 dim의 encoding을 가진 face dataset에 대한 autoencoder model을 훈련한다고 가정
• 이상적인 autoencoder는 관찰을 압축된 표현으로 묘사하기 위해 피부색, 안경 착용 유무 등에 대한 얼굴의 설명적인 속성을 배울 것이다
  
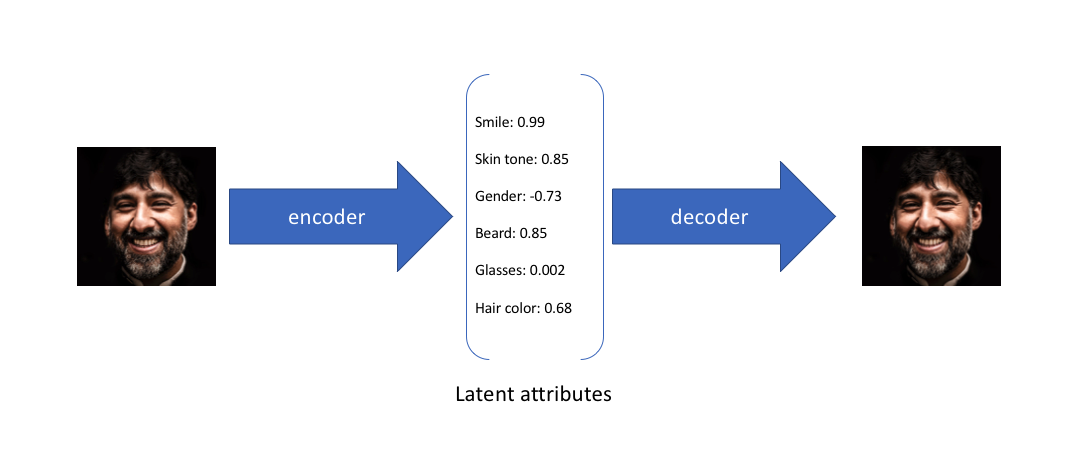
• 위 예시처럼 입력 이미지를 각 속성을 설명하기 위해 single value를 사용하여 latent 속성 관점에서 설명했다
• 그러나 우리는 가능한 값의 범위로 각 잠재 속성을 표현하는 것을 선호할 수 있다
  • 예를 들어, 모나리자 사진을 입력했을 때 smile 속성에 어떤 single value가 할당될 수 있을까?

➡️ Variational autoencoder를 사용하여 latent 속성을 확률론적 term으로 설명 가능하다

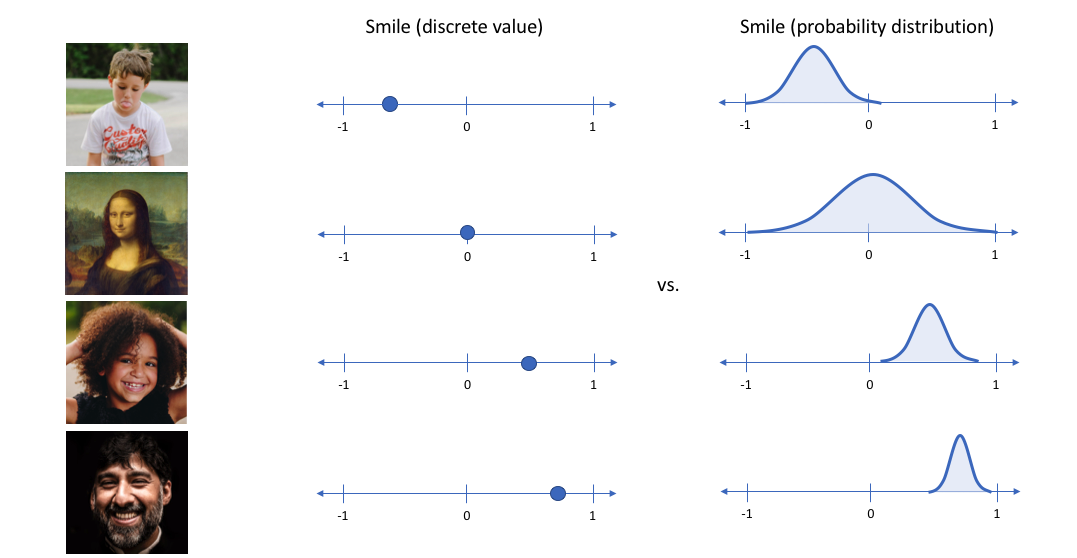
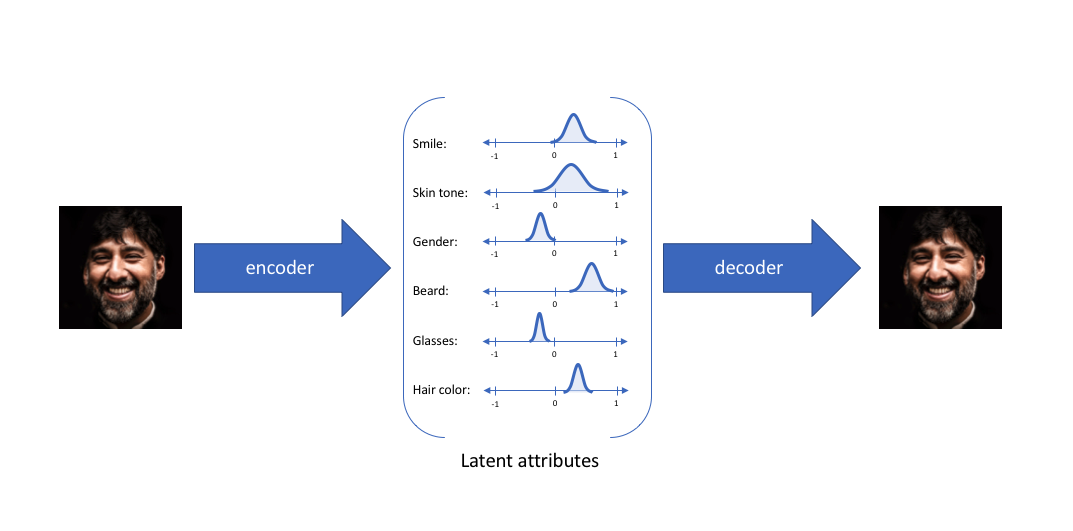
• 이러한 접근으로, 주어진 input에 대해 각 latent attribute를 확률 분포로 표현할 것이다
• latent state로부터 decoding할 때, 각 latent state 분포를 랜덤으로 표본을 추출하여 decoder 모델에 대한 input으로 벡터를 생성할 것이다

• decoder 모델에 입력하기 위해 랜덤으로 샘플링할 수 있는 가능한 값의 범위(통계 분포)를 출력하도록 encoder 모델을 구성함으로써, 근본적으로 지속적이고 매끄러운(continous, smooth) latent space 표현을 시행한다
• decoder 모델이 input을 정확히 재구성할 수 있는 것을 기대하기에, latent space에서 서로 가까운 값을 매우 유사한 재구성과 일치해야 한다

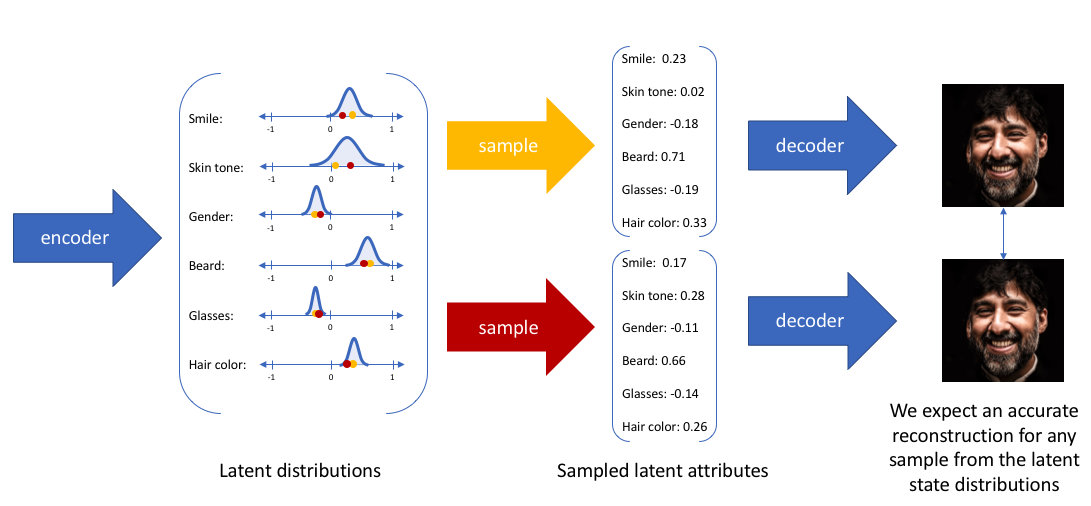
Statisical motivation

• hidden variable $z$ which generates an observation $x$

• $p(z|x)=\frac {p(x|z)p(z)}{p(x)}$

  • but, $p(x)$를 계산하는 것은 꽤 어려움 ➡️ variational inference를 적용하여 풀 수 있다

• 다루기 쉬운(tractable) 분포를 가지는 다른 분포 $q(z|x)$에 의해 $p(z|x)$를 근사한다고 가정해보자

• $q(z|x)$의 파라미터를 $p(z|x)$와 아주 유사하게 정의할 수 있다면, 그것을 다루기 힘든 분포(intractable)에 대한 대략적인 추론을 수행하는 데 사용 가능하다

• KL divergence: 두 확률 분포의 차이를 측정

  • $q(z|x)$가 $p(z|x)$와 유사하다는 것을 확실히 하고자 한다면, 두 분포 사이의 KL divergence를 최소화할 수 있다
  • $\text{min}~\text{KL}(q(z|x)||p(z|x))$ = $\text{max}~E_{q(z|x)}logp(x|z)-KL(q(z|x)||p(z))$
  • $E_{q(z|x)}logp(x|z)$: reconstruction likelihood를 표현
  • $KL(q(z|x)||p(z))$: 학습된 분포 $q$가 실제 prior 분포 $p$와 유사하다는 것을 보장

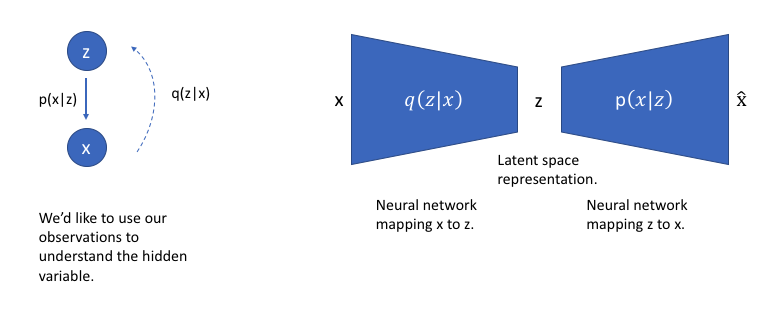
• an observation을 생성하기 위해 사용되는 가능한 hidden variables(ie. latent state)를 추론하기 위해 $q$를 사용할 수 있다

• 이러한 모델을 $x$에서 $z$로의 mapping을 학습하는 encoder 모델과 $z$부터 다시 $x$로의 mapping을 학습하는 decoder 모델을 가진 neural network architecture로 구성할 수 있다

• network 대한 손실 함수 두 개의 항으로 구성된다

  • 하나는 reconstruction error(앞서 논의한 것처럼 reconstruction 가능성을 최대화할 수 있다고 생각할 수 있음)에 패널티를 주는 것

  • 다른 하나는 학습된 분포 $q(z|x)$가 실제 prior 분포 $p(z)$와 유사하도록 장려

    • $p(z)$: latent space의 각 차원 $j$에 대한 Gaussian 분포

    • $L(x, \hat{x}) + \sum_jKL(q_j(z|x)||p(z))$