Kalman Filter

hizikang01·2025년 4월 5일

machine learning

칼만 필터는 루돌프 E. 칼만 (Rudolf E. Kalman) 이라는 수학자/전산학자가 1960년에 제안한 알고리즘임

상태 예측

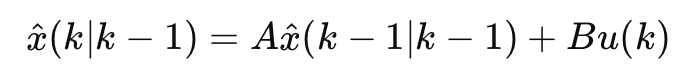
이전 상태에서 시스템이 어떻게 바뀌는지 반영해서 다음 상태를 예측하는 식
ex. 속도가 10이고 1초가 지났으니까, 위치는 10만큼 이동했을거야
오차 공분산 예측

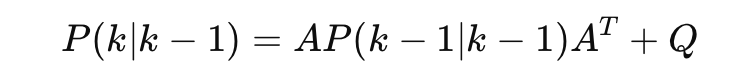
예측된 상태의 불확실성(P)도 같이 예측, 시스템 모델 자체가 부정확 할 수 있으니까 잡음(Q)도 더해줌

2단계: 업데이트 (Update)

칼만 이득 계산

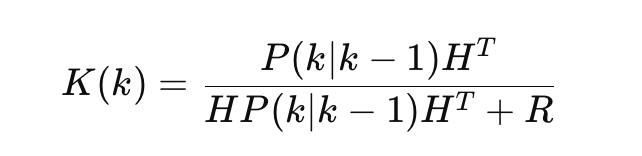
예측값과 관측값 중 누굴 더 믿을지 결정하는 비율
예측이 정확하면 K는 작고, 관측값을 많이 믿음
관측이 정확하면 K는 커지고, 예측을 더 무시함
상태 보정

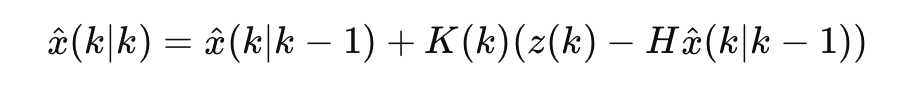
예측값에다가 오차(측정값-예측값)을 더해줌
얼마나 더할지는 K가 결정
오차 공분산 예측

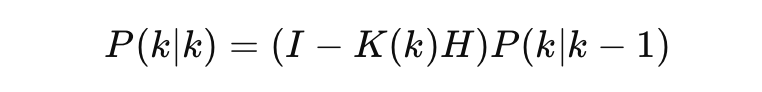
업데이트 후의 불확실성도 갱신, 보정을 잘 했으니까 오차 범위도 줄여줌

과정을 요약하면
예측 : 이쯤있겠지
관측 : 센서는 여기라고 말해
보정 : 둘 사이의 차이를 반영해서 더 정확하게

내가 계산한 값(예측) + 센서가 알려주는 값(관측) = 둘을 잘 섞어서 더 믿을 만한 결과를 만드는 알고리즘

3. 칼만 필터 적용 사례

분야	적용 예시
자율주행차	GPS + IMU 융합, 차 위치 추적
로봇	로봇의 위치와 속도 추정
스마트폰	센서 융합으로 방향, 위치 추정
항공우주	항공기의 고도/속도/위치 추적
금융	주가 예측, 시계열 필터링
게임/AR	카메라, 센서 위치 안정화

4. 칼만 필터 예제 코드 (1D 위치 추정)

import numpy as np
import matplotlib.pyplot as plt

# 초기 상태
x = 0
P = 1
Q = 0.01
R = 1

# 시뮬레이션 데이터
np.random.seed(0)
true_positions = np.linspace(0, 50, 100)
measurements = true_positions + np.random.normal(0, np.sqrt(R), size=100)

estimates = []

for z in measurements:
    # 1. 예측
    x_pred = x
    P_pred = P + Q

    # 2. 업데이트
    K = P_pred / (P_pred + R)
    x = x_pred + K * (z - x_pred)
    P = (1 - K) * P_pred

    estimates.append(x)

# 시각화
plt.plot(true_positions, label='True Position')
plt.plot(measurements, label='Measurements', alpha=0.5)
plt.plot(estimates, label='Kalman Estimate', linewidth=2)
plt.legend()
plt.title("Kalman Filter 1D Position Tracking")
plt.xlabel("Time")
plt.ylabel("Position")
plt.grid(True)
plt.show()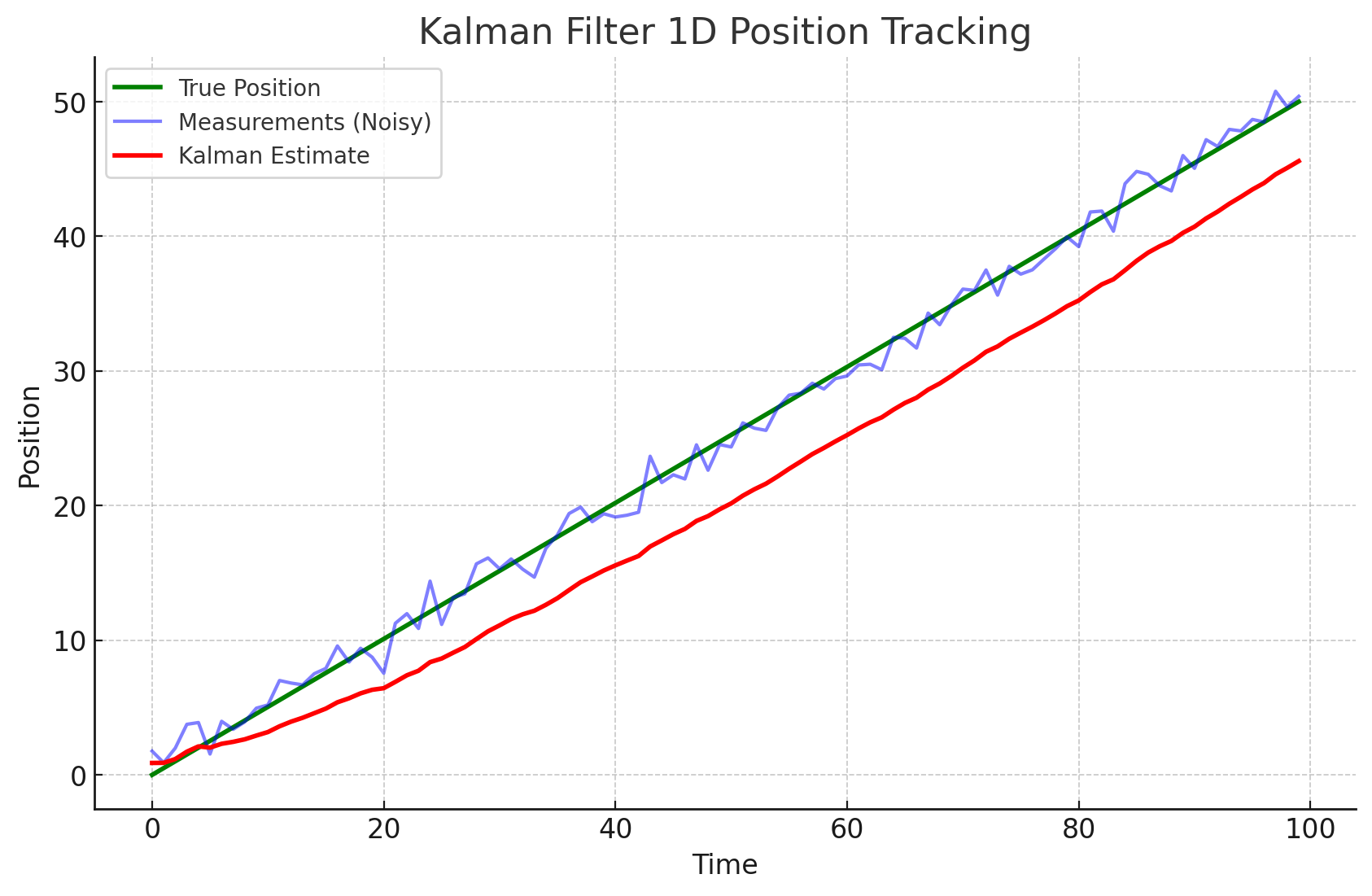

그래프 구성

색상	의미	설명
🟢 초록색 선	`True Position`	실제 위치 (정답값, 기준선)
🔵 파란색 선	`Measurements (Noisy)`	센서로 측정한 값 (잡음 포함)
🔴 빨간색 선	`Kalman Estimate`	칼만 필터가 추정한 위치 (예측 + 보정 결과)

주요 포인트 요약

센서 값(파란 선) 은 들쭉날쭉합니다 → 현실에서 흔한 센서 잡음 상황
칼만 필터 추정값(빨간 선) 은 처음엔 차이가 크지만, 점점 실제 위치(초록 선) 에 가까워집니다
필터가 반복적으로 보정되면서, 보다 부드럽고 정확한 위치 추정이 가능해지는 것을 볼 수 있습니다

칼만 필터는 단순히 센서 값만 믿지 않고,
예측한 값과 센서 값을 적절히 조합해서 오차를 줄이는 방법입니다.
위 그래프는 칼만 필터가 센서보다 얼마나 더 신뢰할 수 있는 추정치를 만들어주는지를 보여줍니다.

5. 추가로 알아두면 좋은 내용 (EKF/UKF 등)

현실 시스템은 대부분 비선형이기 때문에,
기본 칼만 필터로는 정확한 추정이 어려움
그래서 확장 버전이 필요함

EKF (Extended Kalman Filter)

시스템이 선형이 아닐 경우, 테일러 전개를 이용해 선형 근사
미분 가능한 모델에 적합 (야코비안 필요)

UKF (Unscented Kalman Filter)

시그마 포인트 샘플링을 이용해 비선형 시스템을 더 정확히 처리
미분이 필요 없고 예측 성능이 더 뛰어남

비교 요약

필터	특징	비선형 처리 방식	복잡도
KF	선형만 가능	없음	⭐
EKF	근사 가능	미분 (야코비안)	⭐⭐
UKF	정밀	샘플링 기반	⭐⭐⭐

라이브러리 추천

filterpy → KalmanFilter, ExtendedKalmanFilter, UnscentedKalmanFilter 제공
pykalman → 간단한 시계열 예측에 사용 가능

hizikang01

이전 포스트

동기(Synchronous) vs 비동기(Asynchronous)

다음 포스트

Kalman Filter

목차

1. 칼만 필터 개념

🚌 예시: 눈 감고 버스 타기

2. 칼만 필터 작동 원리와 수식

1단계: 예측 (Prediction)