Random Variable
확률에 의해 정해지는 결괏값들
ex) 주사위 던지기
- discrete : ex) 죽냐/사냐
- continuous : ex) 혈압
기댓값

Variance/standard deviation
평균으로부터 떨어진 거리

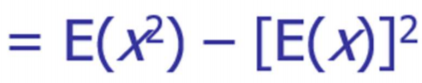
Gaussian
= 정규분포 (종모양)
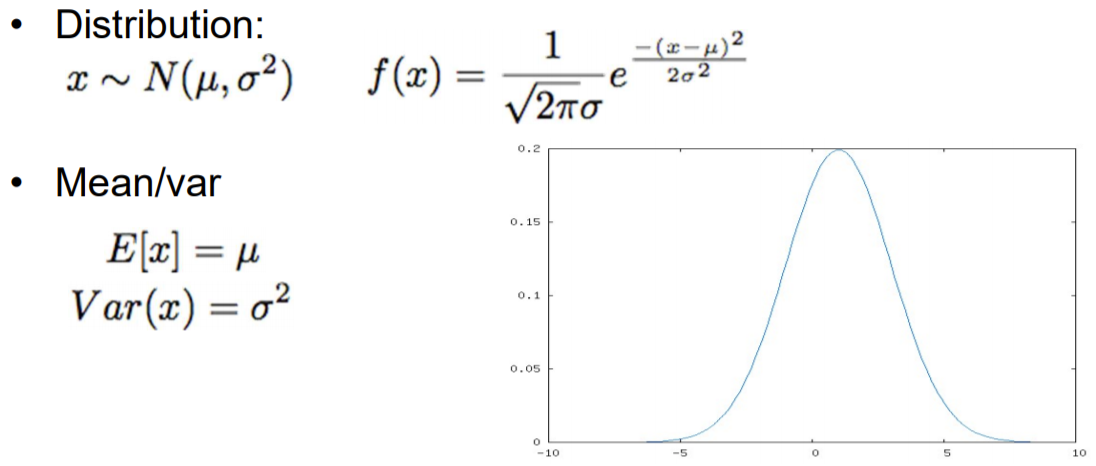
ex) 동전 100번 던질 때 앞면 나오는 확률의 분포
Covariance
두 변수의 선형 관계

x의 편차와 y의 편차를 곱한 평균
즉, 서로 다른 변수들 사이에 얼마나 의존하는지를 수치적으로 표현하며, 그것의 직관적 의미는 어떤 변수(X)가 평균으로부터 증가 또는 감소라는 경향을 보일 때, 이러한 경향을 다른 변수(Y 또는 Z 등등)가 따라 하는 정도를 수치화 한 것


예제 1. X와 Y가 독립일 때 공분산
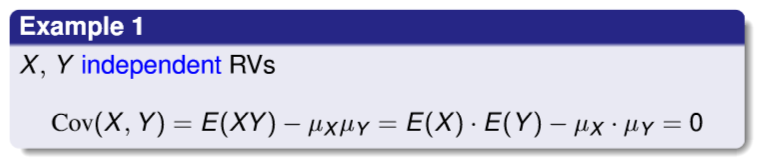
예제 2. 결합 확률 밀도가 주어졌을 때 공분산

시그모이드
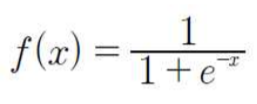
Vector Norms

ex) (0,0) ~ (5,5)
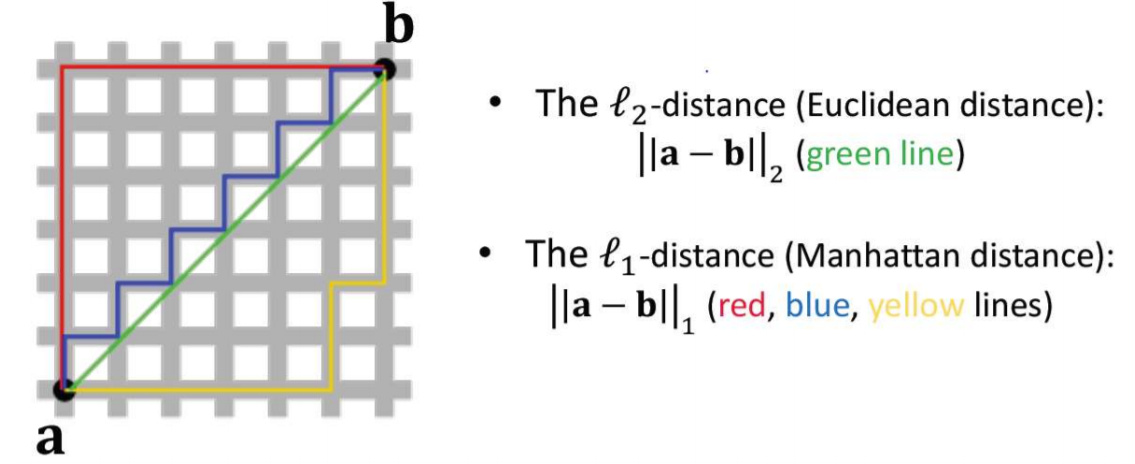
- l1 : 직선 (1차원) (10 거리)
- l2 : 대각선 (2차원) (5 루트 2 거리)
Transpose
=Symmetric

Rank
선형적으로 독립적인 행이나 열의 수 (패턴이 없는 것)
ex) Rank 2 예시
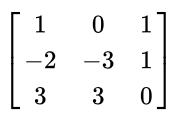
첫번째 열과 두번째 열은 선형 독립이지만, 세번째 열은 첫번째 열에서 두번째 열을 빼면 나오므로, 의존관계여서, Rank 2
Full Rank
모두 독립적
고유 값 (Eigen Value)
- 벡터에 행렬 연산을 취해준다?
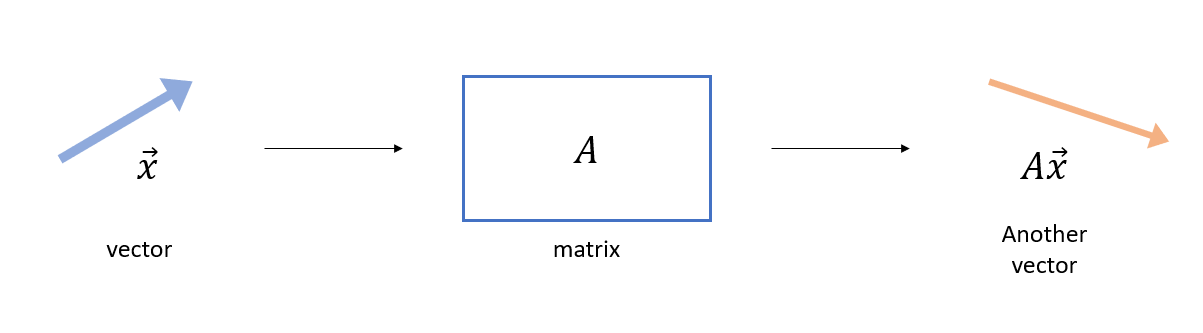
행렬은 벡터를 변환시켜 다른 벡터를 만들어줌!
- vector로
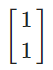
넣고, - matrix로
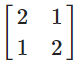
넣는다면,
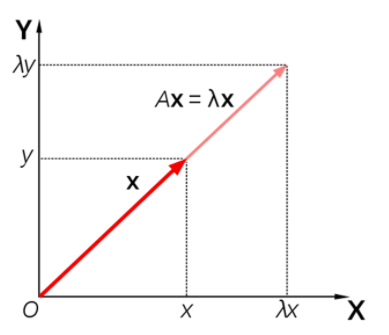
평행하고 크기가 바뀐 벡터 출력
- n x n 행렬 A에서
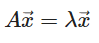
이러한 0이아닌 x벡터가 존재하면,
λ는 A의 고유값이고, x벡터는 고유벡터
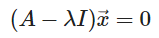
앞에서 x가 0이 아니라고 했으므로,
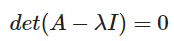
ex)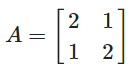
의 고유벡터?
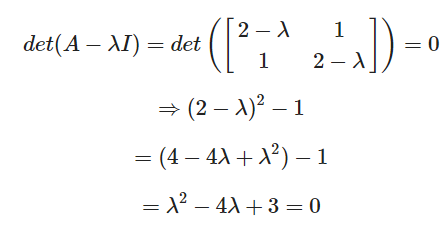
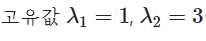
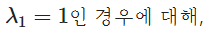
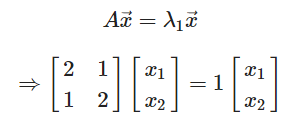
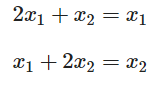

(감마2 = 3도 마찬가지로 구하기)

정보 이론
잘 일어나지 않는 사건이 자주 발생하는 사건보다정보량이 많다라고 함- 독립사건은 추가적인 정보량을 가짐
샤넌의 Entropy
- 확률변수 X의 값이 x인 사건의 정보량
: I(x) = -logP(x)- 이 중, 밑이 10이 아니라 2인 경우 정보량의 단위가 샤년, 또는 비트
ex) 동전을 던져 앞면이 나오는 사건 정보량 : -log2(0.5)=1
ex) 주사위를 던져 눈이 1이 나오는 사건 정보량 : -log2(1/6) = 2.5849
- Shannon's Entropy
: 모든 사건 정보량(밑이 2)의 기대값
H(P) = E[I(x)]
ex) 앞면, 뒷면 나올 확률이 동일한 동전

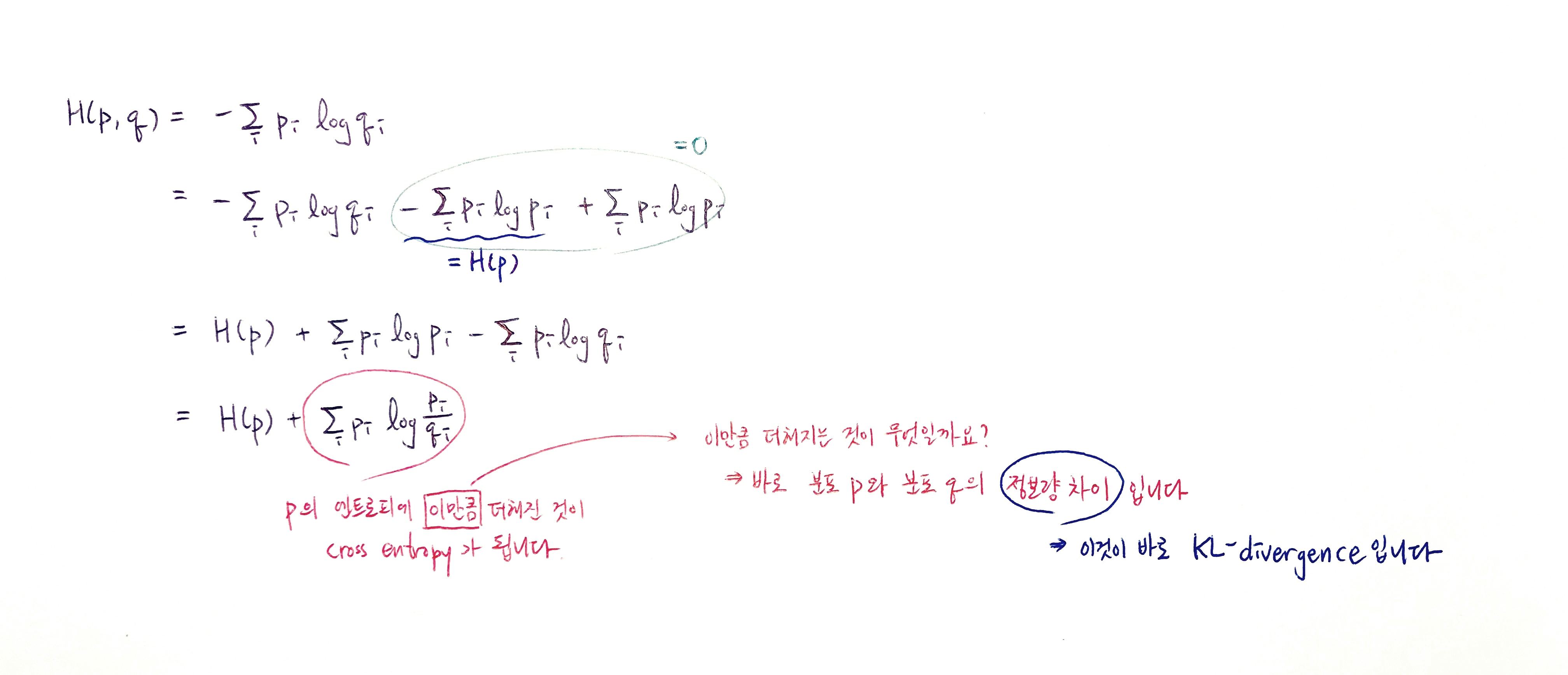
Cross Entropy
실제값과 예측값이 맞는 경우에는 0으로 수렴하고, 값이 틀릴경우에는 값이 커지기 때문에, 실제 값과 예측 값의 차이를 줄이기 위한 엔트로피
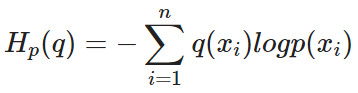
실제 분포
q
에 대하여 알지 못하는 상태에서, 모델링을 통하여 구한 분포인
p
를 통하여
q
를 예측하는 것
KL Divergence
실제 데이터의 분포 P(x)와 모델이 추정한 데이터의 분포 Q(x) 간의 차이 계산