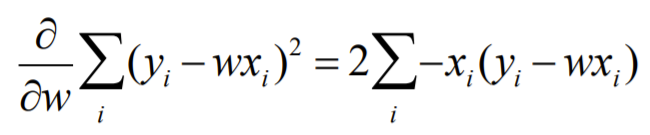
Supervised Learning의 일종
1. Univariate Regression
input(x)와 output(y) 사이의 관계를 직선으로 모델링
ex) 11번가에서 9달러에 파는 물건이 쿠팡에서 얼마에 파는가?

-
파라미터와 노이즈

-
선이 예측 값, 점이 실제 값

-
선과 점 사이의 거리 = error = 최소화해야

그래서 least squares를 쓰는 것
- 그럼 어떻게 최솟값을 구하지?
1) 수학적으로 : 미분

- 매트릭스에서 Linear Regression

2) Gradient Descent
- 알고리즘

Convex
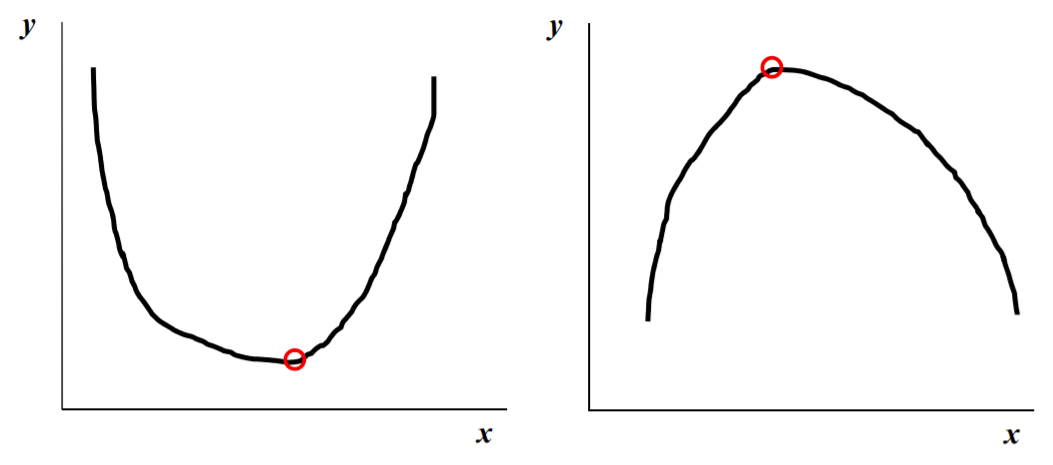
볼록성이 한 개인 경우 (극소나 극댓값이 하나)

- 위와 같이 Non-Convex인 경우, 극솟값이 global minimum은 아닐 수 있음
➡ gradient descent로 최소점 찾기

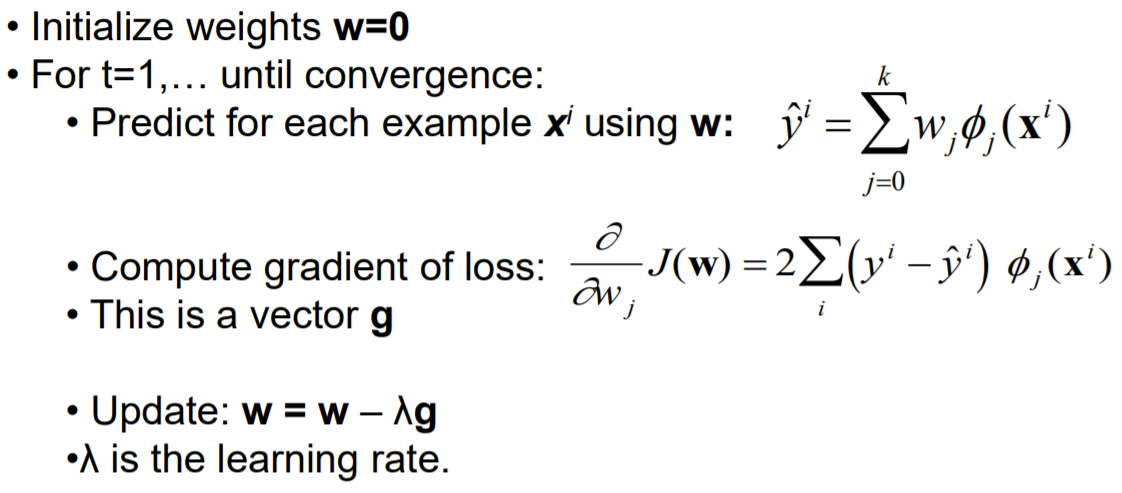
- online processing : 1 at a time
- batch processing : all at once
- mini-batch processing : subset at a time
Stcochastic Gradient Descent (SGD)
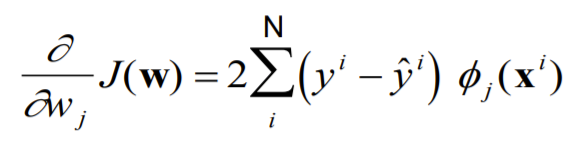
-
전체 데이터 (Batch)가 아닌 일부 데이터의 모음(Mini-Batch)를 사용해서 구한 합
-
Local Minima에 빠지지 않고 Global Minima에 수렴할 가능성이 더 높음
-
정 Local Minima로 빠질까 찜찜하면 두번 미분해서 모양 잡을 수도 있음

2. Multivariate Regression
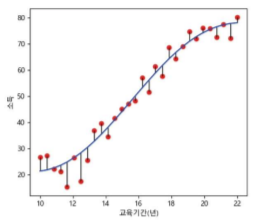
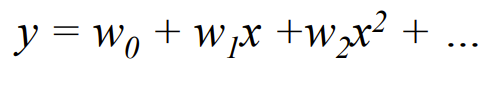
-
보다시피, linear하지 않음
-
둘(이상) input variables 있음
ex) 11번가와 Gmarket으로 쿠팡 값 예측

Linear 아닐 때 Regression 함수 예시

Model Evaluation : Loss Function
- Regression 에서의 손실함수
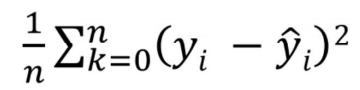
즉,

Error 분석 : Bias and Variance
- Bias : 예측한 값의 평균(E(y-hat))과 실제값(y)의 차이로, 모델이 맞추지 못하는 부분
- Variance : 모델을 통해 예측한 값(y-hat)이 예측값의 평균(E(y-hat))을 중심으로 얼마나 퍼져있는지



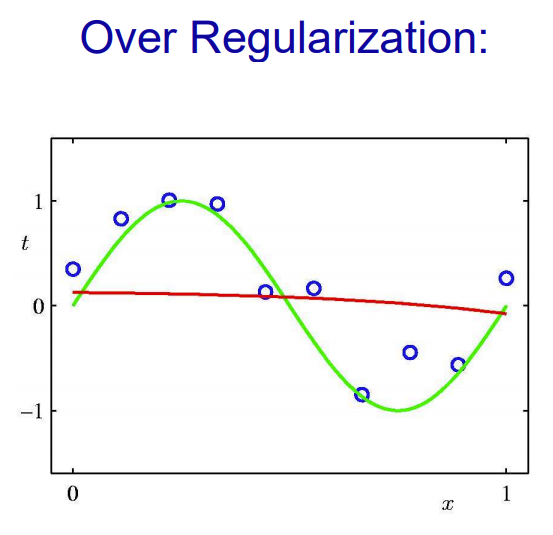
Regularization
- 선형 모델의 과적합을 방지하기 위해 고안된 방법
- 과적합된 모델은 특성들이 너무 복잡하게 적용되어 있어 일어남. 따라서 현재 특성을 줄이거나 특성들의 영향력을 최소화하는 방법이 필요함. 그렇게 고안된 것이 규제 선형모델
- 과적합된 모델은 보통 분산이 높고, 편향이 낮음.(훈련 모델만 그대로 따라가니까) 따라서 분산 정도를 줄여주기 위해 특성치들을 규제하여 사용. 규제는 정규화라고도 불림


-
Lasso
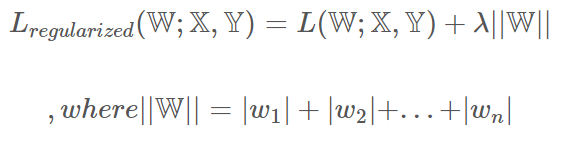
L1 norm을 미분하면, sign 함수가 나오며, 이는 각 요소별로 양수면 1, 음수면 -1을 반환한다. 0이 된 weight를 제거함으로써 완전연결을 희소연결로 바꾸어 overfitting을 방지하는 기능
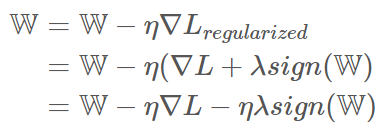
- L1을 규제하는 것. - 손실함수에 L1 Norm 값을 더해 해당 값이 최소가 되도록 함. - L1 Norm 값 앞에 gamma값(사람이 지정한 값)을 부여해 조절해서 사용. - 가중치의 모든 원소에 똑같은 힘으로 규제를 함. -
Ridge
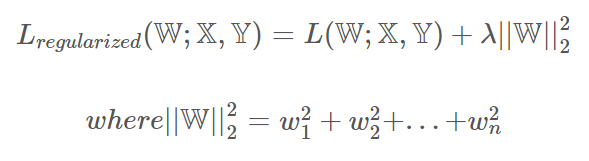
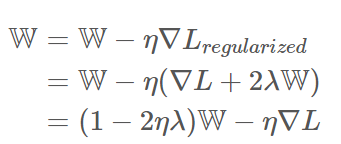
- L2를 규제하는 것. 손실함수에 L2 Norm 값을 더해 해당 값이 최소가 되도록 함. - L2 Norm 값 앞에 gamma값 부여해 조절해서 사용. - 모든 원소에 골고루 규제를 적용해 0에 가깝게 만듦 - W값을 2ηλ 만큼 축소시키고, −η∇L 만큼 더하는 효과를 준다. - 이런 과정을 반복하면 결국, 최종 해를 원점 가까이 당기는 효과가 난다. - 한편, L2 규제로 만들어진 L2 loss는 제곱항의 효과로 outlier(피팅된 함수에서 멀리 분포된 몇몇의 데이터)에 영향을 많이 받는다. - 그래서 L1 loss는 L2 loss보다 outlier에 더 robust(둔감) 하다고 할 수 있다. - 따라서 outlier가 적당히 무시되길 원하면 L1 loss, outlier의 등장에 신경을 써야한다면 L2 loss를 선택하면 된다.
Optimization
최적값이 나올 때까지 찾기
