Ensemble Learning
-
한 전문가의 의견보다 여러 사람의 종합된 의견이 더 나은 경우가 많다
= 하나의 좋은 예측기보다 보통 예측기 집단의 예측이 더 낫다 -
방법
👍 Bagging (Majority Voting / Bagging / Random forest)
👍 Boosting (AdaBoost, Gradient Boost)
👍 Stacking
-
앙상블을 통한 변동성 축소
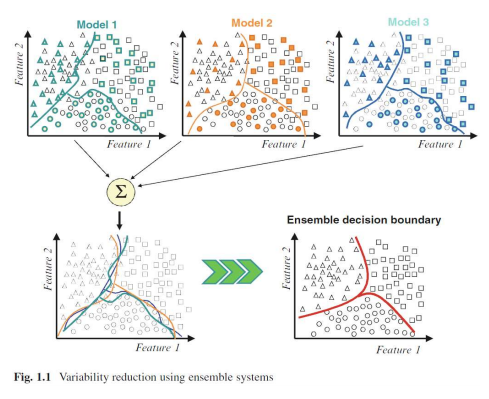
분류기들의 오류가 각 샘플에 대해 다른 오류를 발생시키지만 옳은 분류에 대해서는
일반적으로 일치한다고 가정할 때, 앙상블의 분류기 출력을 Averaging 하는 것은 오류
요소들이 averaging out 되게 만들어 앙상블 모델 오류를 감소시킴
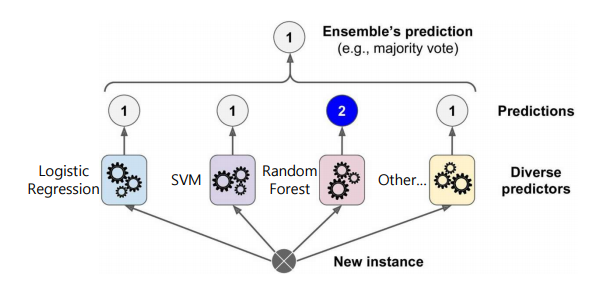
1. Voting Classifiers
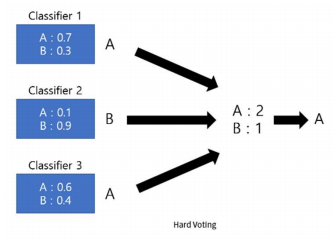
- Hard Voting Classifier
- 여러 개의 classifier들을 이용하여 다수결에 따른 예측을 하는 분류기
- 앙상블 내의 가장 우수한 분류기보다 좋은 결과를 내기도 함
-
Soft Voting Classifier
확률의 평균에 의한 선택
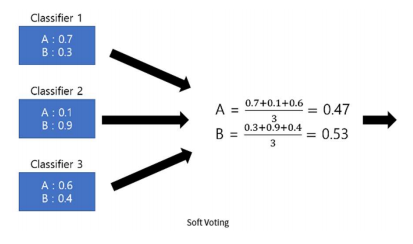
➡ B 선택 -
Weak Learner와 Strong Learner
- Weak Learner : 정확도가 50%보다 약간 좋은 정도
- Strong Learner : 70% 이상? 80% 이상?
👍 각 분류기가 모두 weak learner이더라도 앙상블은 strong learner가 될 수 있음
🤷♀️ 큰 수의 법칙 때문
앞 면이 나올 확률이 51%인 동전을 1000번 던질 때, 앞 면이 과반일 확률 = 75%
10000번 던지면 97%
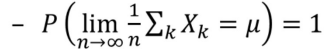
실험횟수가 무한히 증가할수록 표본 평균은 모집단 평균에 가까워짐
- 다양성 확보 방법
- classifier 섞어 쓰기 (Hard voting & Soft voting classifiers)
- 훈련 데이터의 서로 다른 부분집합들을 사용
- 서로 다른 샘플링 방법들을 사용 (부트스트래핑이면 배깅, 이전에 오분류된 샘플들을 선호하는 분포에서 샘플링하는 거면 부스팅)
- 가용한 feature들의 서로 다른 부분집합을 사용 = random subspace methods
- Base classifier에 서로 다른 파라미터들을 적용
- 여러 가지 다른 형태의 다양성 측도가 있으나, 앙상블 정확도와의 구체적 관계는 아직 밝혀지지 않고 있음
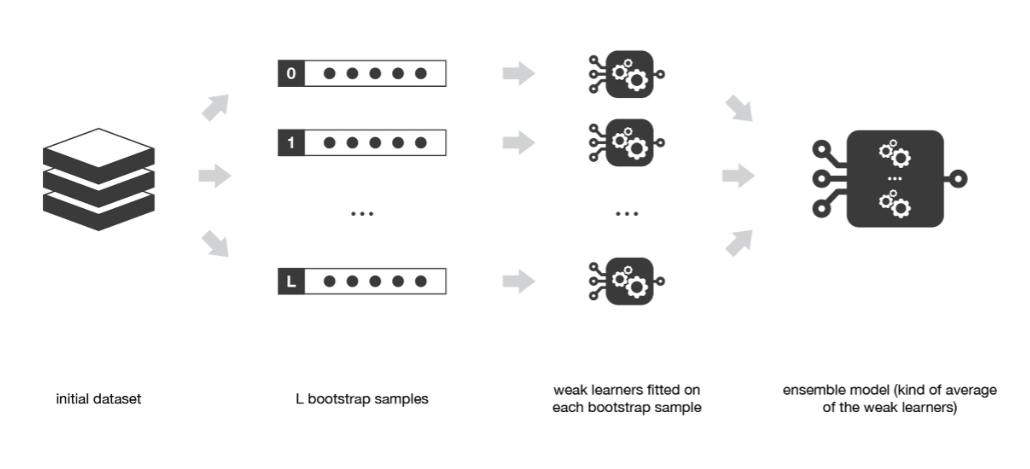
2. Bagging과 Pasting
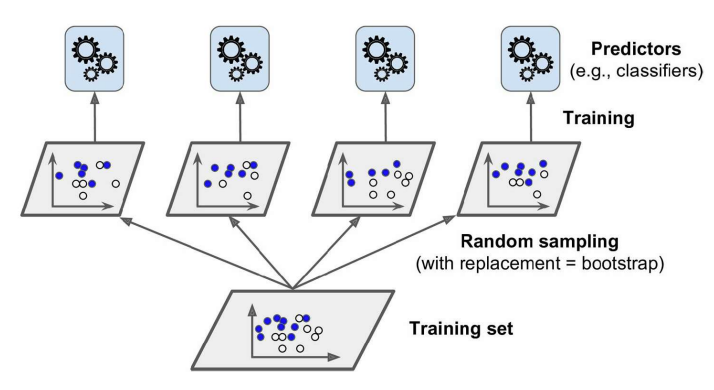
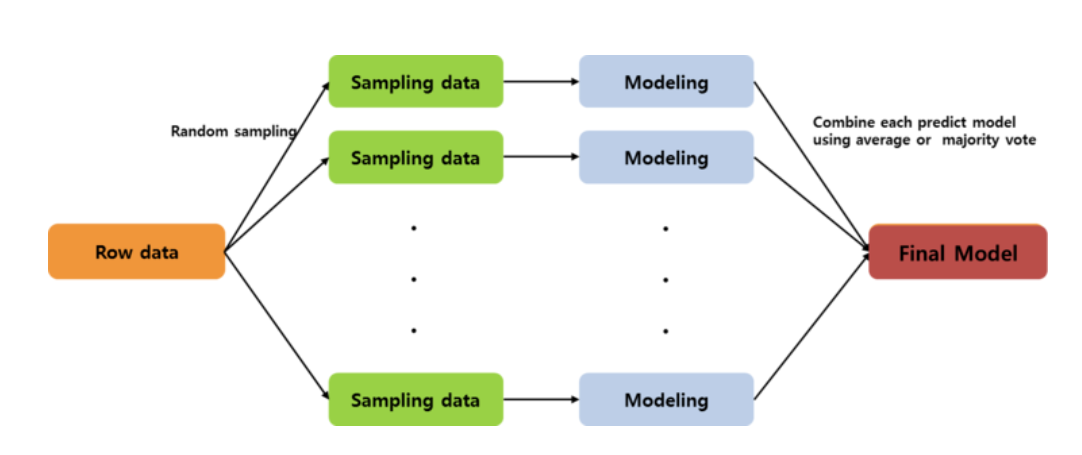
무작위로 훈련 데이터 셋을 잘게 나눈 후 나누어진 훈련 데이터 셋을 여러 개의 모델에 할당하여 학습 후, 각 샘플의 모델링을 통해 나온 예측 변수들을 결합해서 최종 모델 생성
- 배깅 : 중복을 허용하며 훈련 데이터 셋을 나눔 (= Bootstrap, 중복(replacement)이 허용된 리샘플링) ➡ 변동성 (분산)이 줄어듦
전체 훈련 데이터에서 여러 번 중복을 허용한 복원 추출을 함
✍ Bootstrap
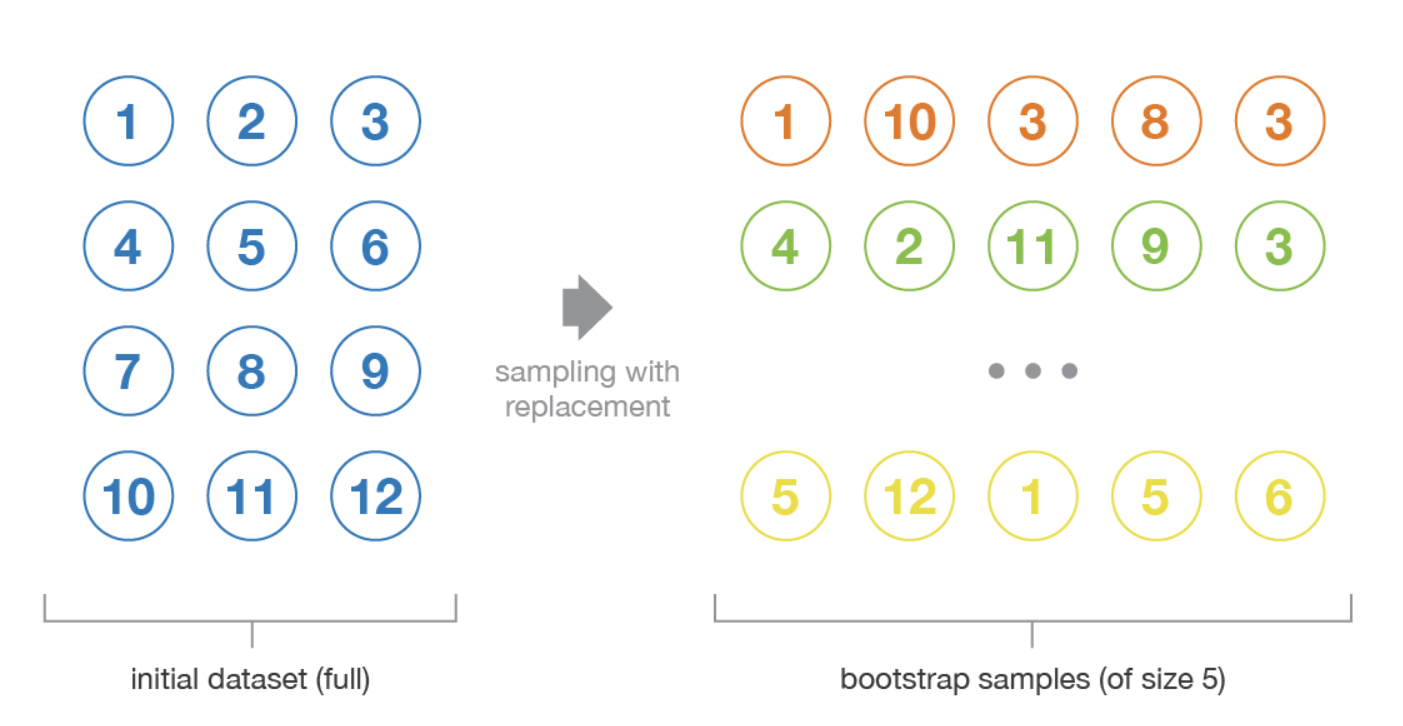
- 페이스팅 : 중복을 허용하지 않고 훈련 데이터 셋을 나눔
ex) {1,2,3,1,2,1,1,1} (n = 8) 배깅하기
• {1,2,1,2,1,1,3} (n = 8); mean = 1.375
• {1,1,2,2,3,1,1} (n = 8); mean = 1.375
• {1,2,1,2,1,1,2} (n = 8); mean = 1.25
로 부트스트래핑 하기
그렇다면, 최종적으로 (1.375+1.375+1.25)/3 = ~1.3333
- 어떻게 마지막 모델로 샘플링된 모델들 결합?
- 분류 모델(목표 모델이 범주형)이면 Statistical Mode (최빈값, 다수결)
- 회귀 모델(목표 모델이 연속형)이면 Average (평균값)
- 개별 predictor는 원래 훈련 데이터셋에서 학습한 것보다 bias가 더 높게 나옴
- 마지막 결합을 통해 bias, variance를 모두 줄일 수 있음
-
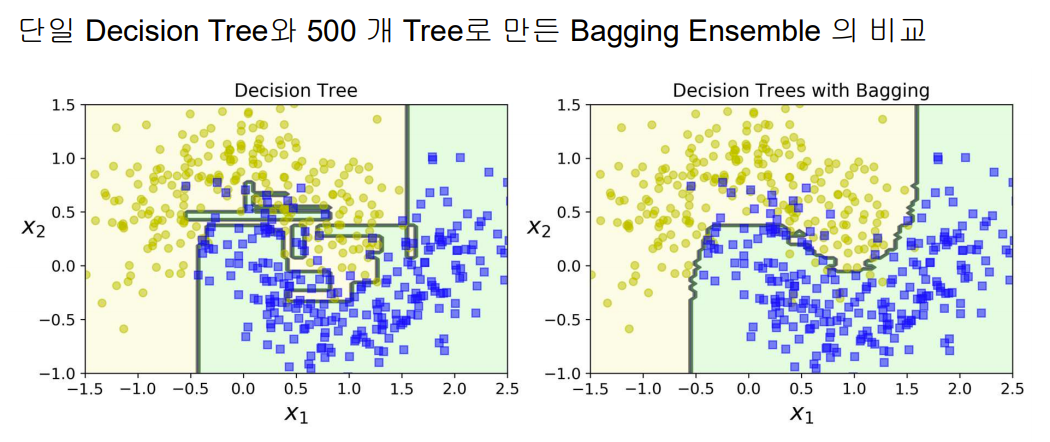
Bootstrapping 은 각 predictor 가 훈련하는 부분집합의 다양성을 증가시키므로 Bagging 이 Pasting 보다 Bias 가 약간 더 높아짐(predictor 들 간의 상관관계를 줄여줌) ⟹ 앙상블의 variance 를 줄여줌.
-
일반적으로 Pasting 보다 Bagging 의 결과가 더 나음.
-
Out Of Bag Evaluation
✅ Bootstrap에서 평균적으로 63%의 사례만 추출되고 나머지 37%는 훈련에 사용되지 않고 남아 있게 됨
🤷♀️ m개의 샘플 중에서 무작위로 하나를 추출할 때 선택되지 않고 남아 있을을 확률은
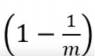
따라서, m번 추출해도 선택되지 않을 확률은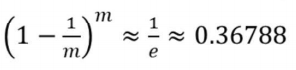
✅ 별도의 validation set 또는 cross validation없이 oob 사례들로 앙상블을 평가할 수 있음
- 앙상블의 evaluation score는 각 predictor의 oob evaluation 결과의 평균
✅ 트레이닝 데이터를 선택하는 방법에 따라 다음과 같이 부르기도 한다.
- Pasting: 같은 데이터 샘플을 중복사용(replacement)하지 않음
- Bagging: 같은 데이터 샘플을 중복사용(replacement)
다음 두개는 가용한 feature 들의 서로 다른 부분집합을 사용하여 다양성 확보하는 방법, Bias 는 약간 커지는 대신 variance 를 낮출 수 있음, 이미지 처럼 고차원 입력 데이터를 다룰 때 유용
- Random Subspaces: 데이터가 아니라 다차원 독립 변수 중 일부 차원을 선택하는 경우
훈련 데이터는 그대로 두고 feature 들만 샘플링하는 방법
bootstrap=False
max_samples=1.0
bootstrap_features=True
max_features=추출 특징 수 또는 0.0 ~ 1.0 사이 값
Random Patches: 데이터 샘플과 독립 변수 차원 모두 일부만 랜덤하게 사용
훈련 데이터와 feature(특징/속성) 모두를 샘플링 하는 방법
bootstrap=True
max_samples=추출 표본 수 또는 0.0 ~ 1.0 사이 값
bootstrap_features=True
max_features=추출 특징 수 또는 0.0 ~ 1.0 사이 값
✅ 배깅에서 Decision Tree를 사용할 때의 한계
- Decison tree는 훈련된 특정 데이트에 민감해서 훈련 데이터가 변경되면 decision tree의 결과(예측)는 상당히 달라질 수 있다.
- 훈련시키는데 computationally expensive하고 overfitting 위험이 있고, local optima를 찾는 경향이 있다(쪼개진 후 그 전으로 돌아갈 수 없어서)
3. Random Forest
Bagging (또는 Pasting) 방법을 적용한 Decision Tree 의 Ensemble
✔ bagging 테크닉이다 (not a boosting technique)
- 결정 트리의 단점은 훈련 데이터에 오버피팅이 되는 경향이 있다는 것
- 여러 개의 결정 트리를 통해 랜덤 포레스트를 만들면 오버피팅 되는 단점을 해결할 수 있음
- 예를들어, 건강의 위험도를 예측하기 위해서는 많은 요소를 고려해야 함.
성별, 키, 몸무게, 지역, 운동량, 흡연유무, 음주 여부, 혈당, 근육량, 기초 대사량 등등등... 수많은 요소가 필요할 것이지만, 이렇게 수많은 요소(Feature)를 기반으로 건강의 위험도(Label)를 예측한다면 분명 오버피팅이 일어남.
예를 들어 Feature가 30개라고 하면, 30개의 Feature를 기반으로 하나의 결정 트리를 만든다면 트리의 가지가 많아질 것이고, 이는 오버피팅의 결과를 야기. 하지만 30개의 Feature 중 랜덤으로 5개의 Feature만 선택해서 하나의 결정 트리를 만들고, 또 30개 중 랜덤으로 5개의 Feature를 선택해서 또 다른 결정 트리를 만들고...
💛 30개의 feature가 있을 때, 분류에서는 보통 √30개가 좋은 feature 개수이고, 회귀에서는 30/3 = 10개가 좋은 feature 선택 개수
이렇게 계속 반복하여 여러 개의 결정 트리를 만들 수 있고, 결정 트리 하나마다 예측 값을 내놓을텐데 여러 결정 트리들이 내린 예측 값들 중 가장 많이 나온 값을 최종 예측값으로 정함. 바로, 다수결의 원칙에 따르는 것.
이렇게 의견을 통합하거나 여러 가지 결과를 합치는 방식을 앙상블(Ensemble)이라고 함
즉, 하나의 거대한 (깊이가 깊은) 결정 트리를 만드는 것이 아니라 여러 개의 작은 결정 트리를 만드는 것이고, 여러 개의 작은 결정 트리가 예측한 값들 중 가장 많은 값(분류일 경우) 혹은 평균값(회귀일 경우)을 최종 예측 값으로 정함. 문제를 풀 때도 한 명의 똑똑한 사람보다 100 명의 평범한 사람이 더 잘 푸는 원리
✅ Bias 는 약간 높아지지만 variance 는 낮아짐
Extra Trees
Extremely Randomized Tree ensemble
- 무작위로 선택한 feature subset 에서 최적의 threshold를 찾아서 분할하는 대신, 무작위성(다양성)을 더하기 위해 random threshold 를 사용하여 분할
- Bias 는 약간 높아지지만 Variance 는 낮아짐.
- 보통의 Random Forest 보다 빠름 ⟸ Optimal threshold 를 찾는 것이 tree growing 에서 가장 시간이 많이 걸리는 부분임.
• RandomForestClassifier 와 ExtraTreesClassifier 중 선택 ?
👀 둘 다 수행해 보고, Grid search 를 사용하여 hyperparameter 튜닝해 가며 cross validation으로 비교해 봐야 한다
Random Forest의 feature 중요도


4. Boosting
여러 개의 weak learner를 결합하여 하나의 strong learner를 만들 수 있는 앙상블 방법
✔ Predictor들을 순차적으로 훈련시키되, 현재 predictor는 이전 predictor 의 잘못을 바로 잡으려고 하는 것이 특징(hypothesis boosting)
✔ AdaBoost(Adaptive) - Gradient(GBM) - XGboost - Light GBM 순으로 좋음
1) Adaboost
이전 예측기가 오분류한 사례들에 더 주의를 기울임으로써 이전 예측기를 바로 잡는 방법
1. 첫 번째 예측기가 오분류한 사례들의 상대적 가중치를 높이고 (boosting)
2. 두 번째 예측기는 1단계를 거친 후, 가중치가 높아진 사례들을 더 잘 분류할 수 있게 됨
3. 다시 두 번째 예측기가 오분류한 사례들의 상대적 가중치를 높이고
⁞
반복
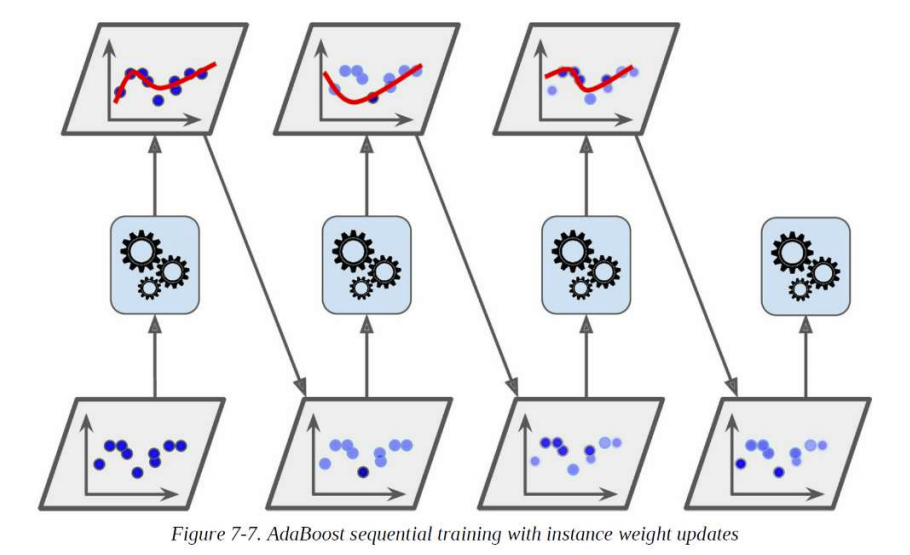
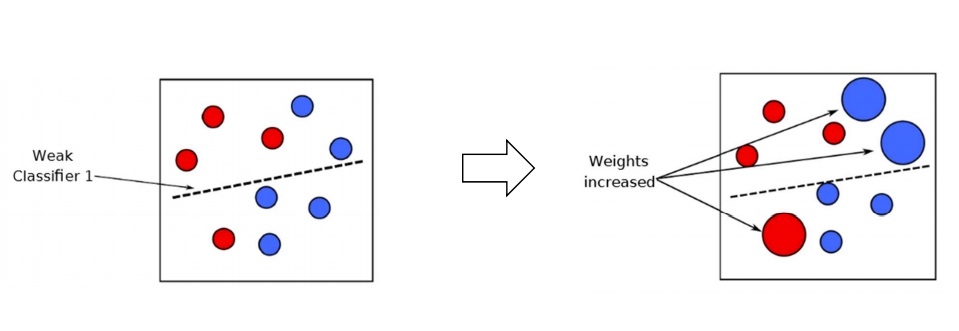
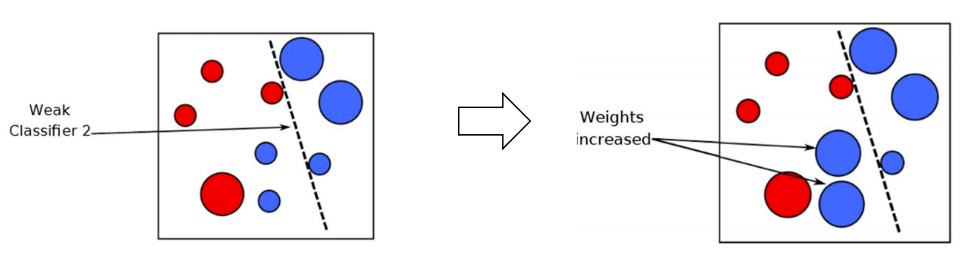
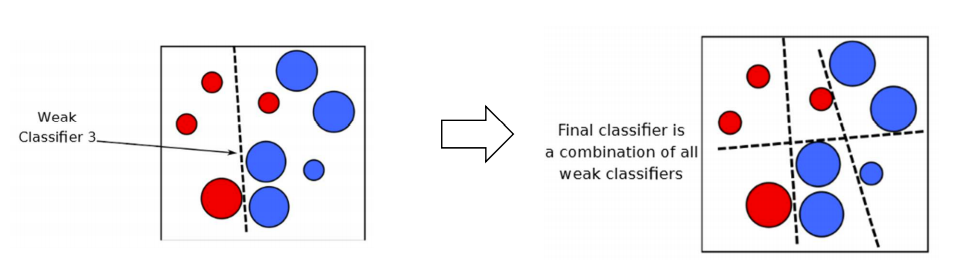
- 연속된 = 순차적 = Adaboost
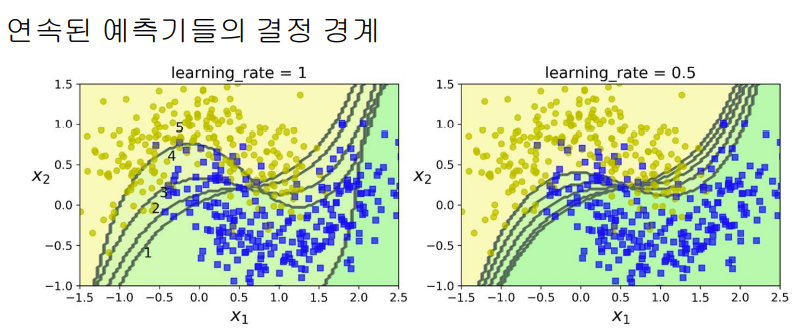
- 순차적 학습 기법은 Gradient Descent 방법과 유사성이 있다.
- Gradient Descent 방법에서는 단일 예측기의 파라미터들을 조정하지만, Adaboost는 점차 좋아지도록 앙상블에 예측기를 추가한다.
- 훈련을 마치면, 앙상블은 사례에 대해서 bagging이나 pasting과 비슷한 방법으로 예측한다. 단, 각 예측기는 가중된 훈련 데이터셋에 대한 정확도에 따라 다른 가중치를 지니고 있다.
-
단점
Bagging 이나 Pasting 처럼 병렬 처리에 의한 고속 처리를 할 수 없다. -
알고리즘

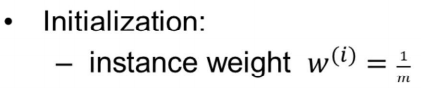


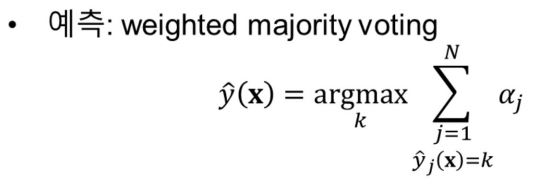
-
SAMME
(Stagewise Additive Modeling using a Multiclass Exponential loss function)
- Scikit-Learn 에서 사용되는 AdaBoost 의 multiclass version 알고리즘
- Binary class 인 경우에는 AdaBoost 와 동일
- SAMME.R : SAMME의 변형으로서, Predictor 가 클래스 확률을 출력할 수 있는 경우(즉, predict_proba() 메소드) 사용할 수 있으며, SAMME 보다 결과가 더 좋다. -
AdaBoostClassifier with Decision Stump
- Decision Stump
max_depth = 1 인 decision tree (한 개의 root node와 두 개의 leaf node)로서 AdaBoostClassifier의 base classifier (Regression 인 경우: AdaBoostRegressor)
-
AdaBoost 가 Overfitting 하는 경우
- Predictor 의 수를 줄인다.
- Base classifier 의 regularization 을 강화한다.
예제 : Chest Pain, Blocked Arteries, Patient Weight에 따른 Heart Disease 여부에 대한 데이터
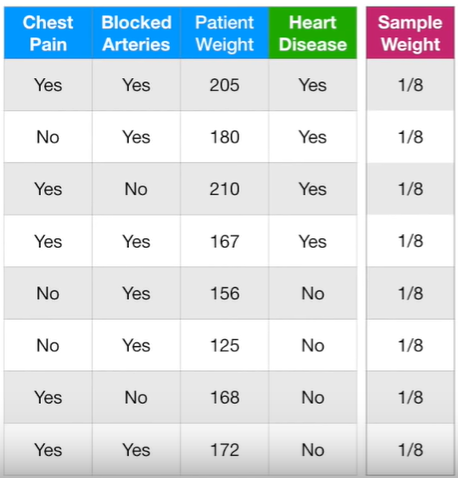
1. 맨 처음 가중치는 모두 1/8

2. Chest Pain과 Heart Disease 관계 모델
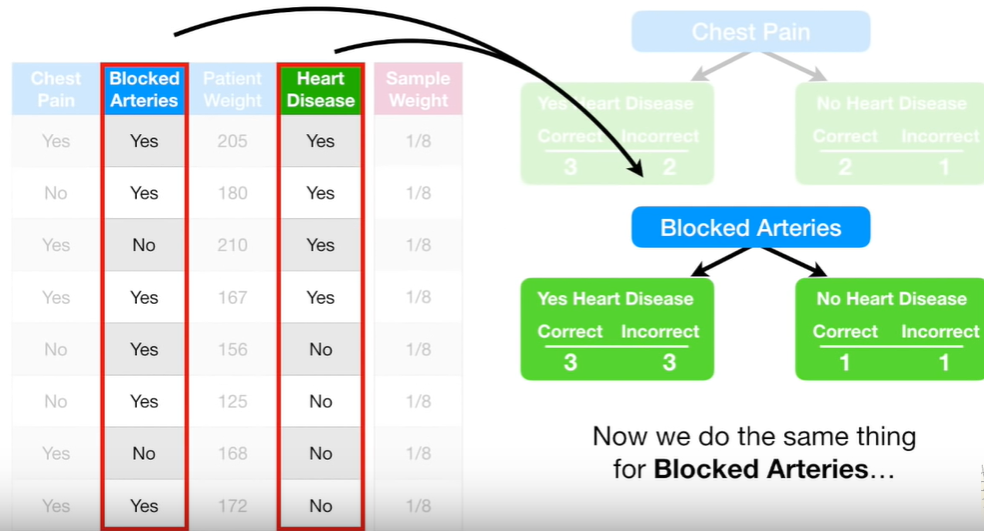
3. Blocked Arteries와 Heart Disease의 관계

4. Patient Weight와 Heart Disease의 관계
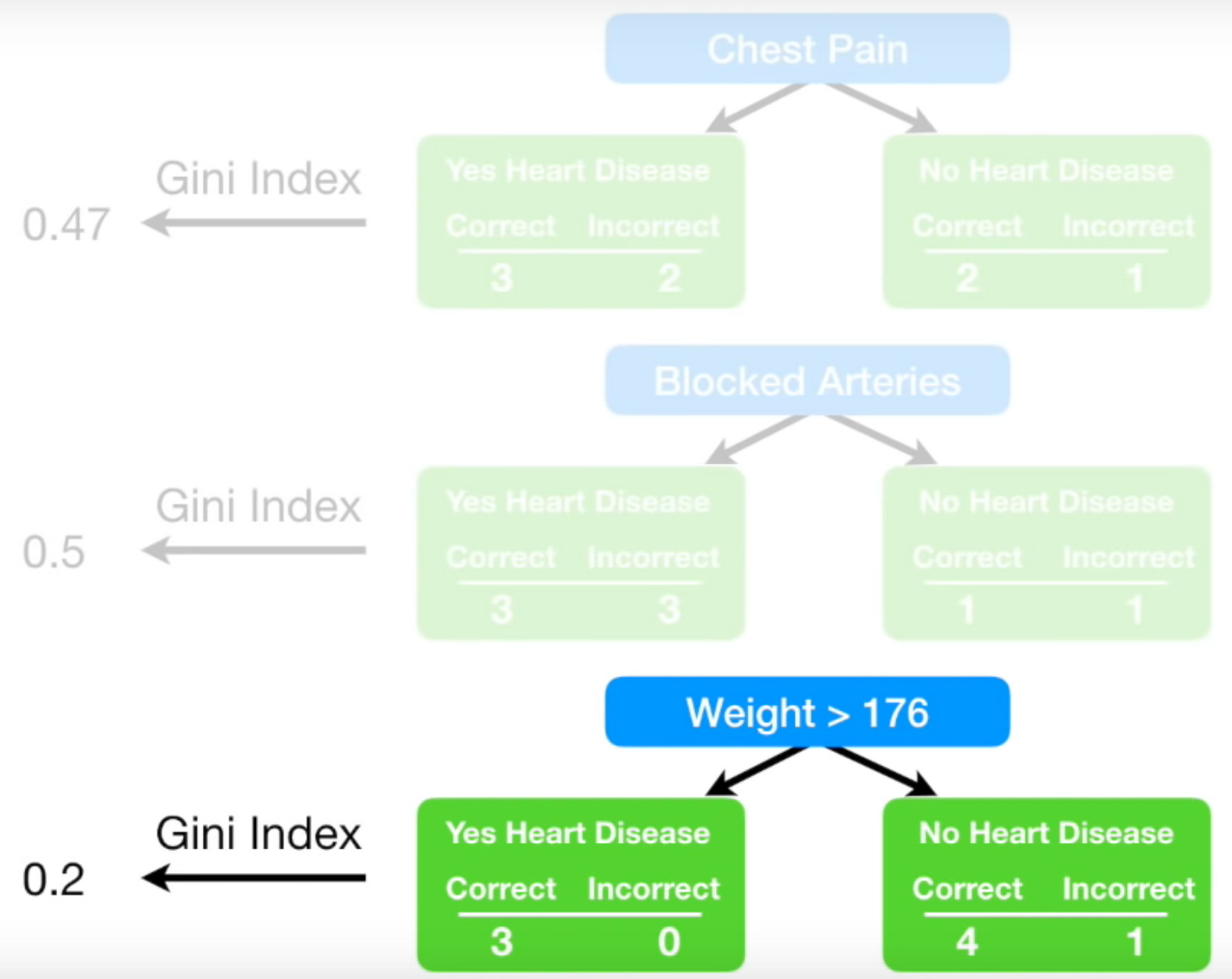
5. 그렇게 각 stump의 지니계수를 구해보니, Patient Weight가 Gini Index가 가장 작아, forest의 첫 stump로 지정
6. Amount of Say 구하기
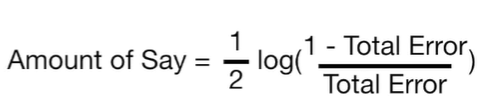
최종 분류에 있어서 해당 Stump가 얼마만큼의 영향을 주는가
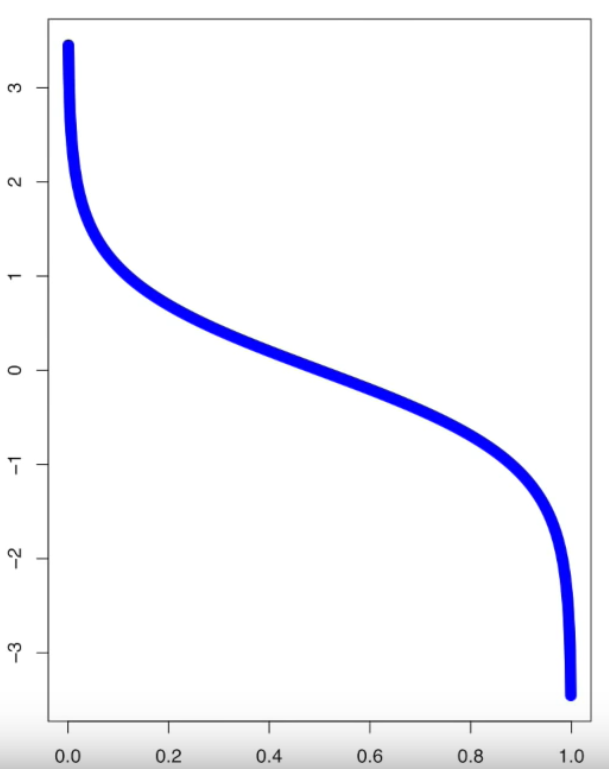
x축은 Total Error, y축은 Amount Of Say로, Total Error가 0이면(=정확성이 높으면) Amount of Say가 큼
이를테면, Weight에서 한개 틀렸으니까 Total Error는 1/8이라서
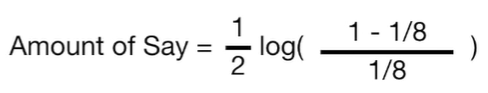
7. 잘못분류한 것에 대해서,

가중치를 위의 식처럼 높여줌
(이전 stump에서 잘못 분류된 sample의) New Sample Weight = (1/8) x e^(0.97) = (1/8) x 2.64 = 0.33 기존의 sample weight = 1/8 = 0.125였는데 이보다 더 높아진 것
8. 잘 분류한 것에 대해서,

amount of say에 - 부호만 붙이면 됨.
(이전 stump에서 잘 분류된 sample의) New Sample Weight = (1/8) e^(-0.97) = (1/8) 0.38 = 0.05. 기존의 weight인 0.125보다 더 작아진 것.
9. Weight의 합은 항상 1이어야 하므로, 정규화 시켜줌
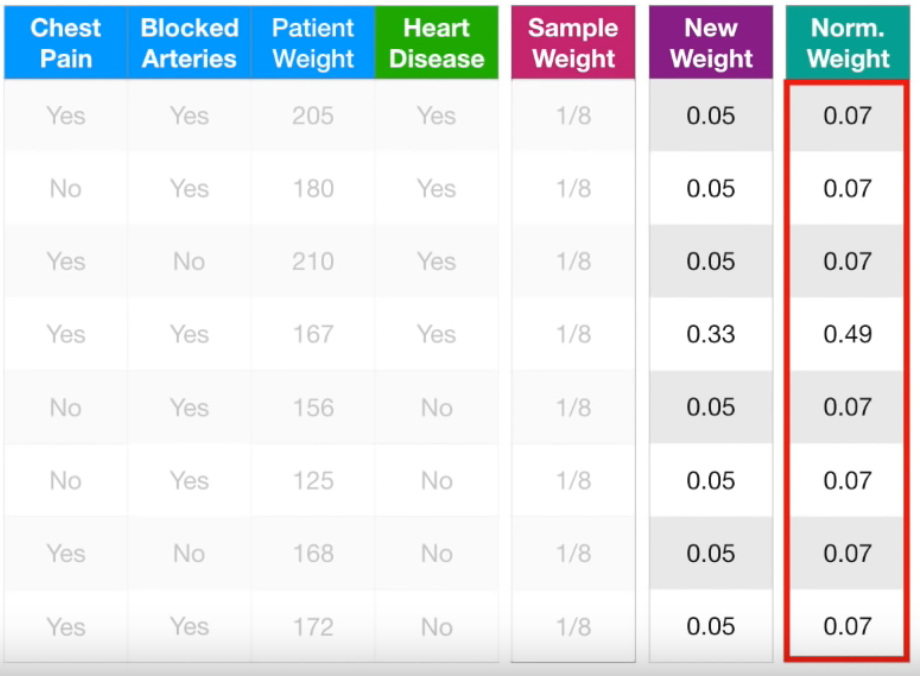
10. 최종분류
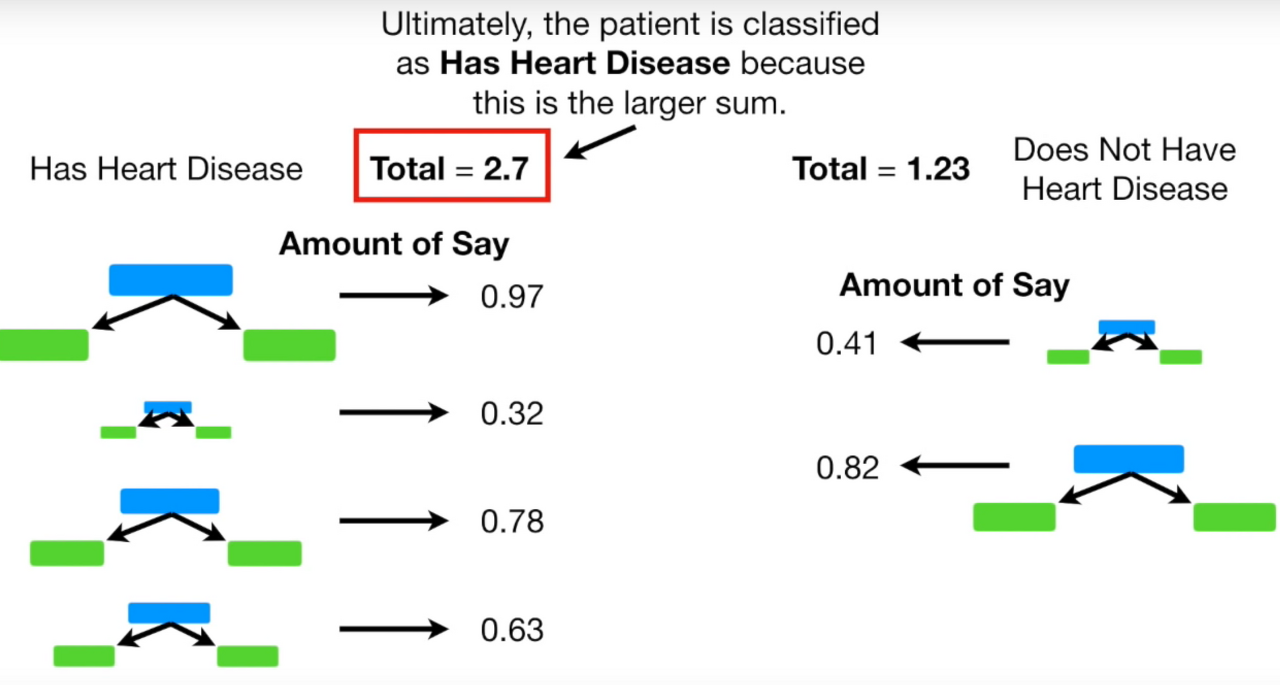
이렇게 여러 차례 진행을 하면 각 Stump마다의 Amount of Say가 나옴. 왼쪽은 Heart Disease가 있다고 판단한 Stump이고, 오른쪽은 Heart Disease가 없다고 판단한 Stump
각 Stump의 Amount of Say를 더하면 Total Amount of Say가 나오고, 이 예시의 경우 Heart Disease가 있다는 것의 Total Amount of Say가 2.7로 더 크므로, 최종적으로 Heart Disease가 있다고 분류를 할 수 있음.
😒 Adaboost와 Gradient Boost 차이점
AdaBoost는 stump로 구성되어 있음. 하나의 stump에서 발생한 error가 다음 stump에 영향을 주고, ... 이런식으로 여러 stump가 순차적으로 연결되어 최종 결과를 도출함
반면, Gradient Boost는 stump나 tree가 아닌 하나의 leaf (single leaf)부터 시작
이 leaf는 타겟 값에 대한 초기 추정 값을 나타내고, 보통은 초기 추정 값을 평균으로 정함.
그 다음은 AdaBoost와 동일하게 이전 tree의 error는 다음 tree에 영향을 줌. 하지만 AdaBoost와 다르게 stump가 아닌, tree로 구성
보통은 leaf가 8개에서 32개되는 tree로 구성
2) Gradient boost


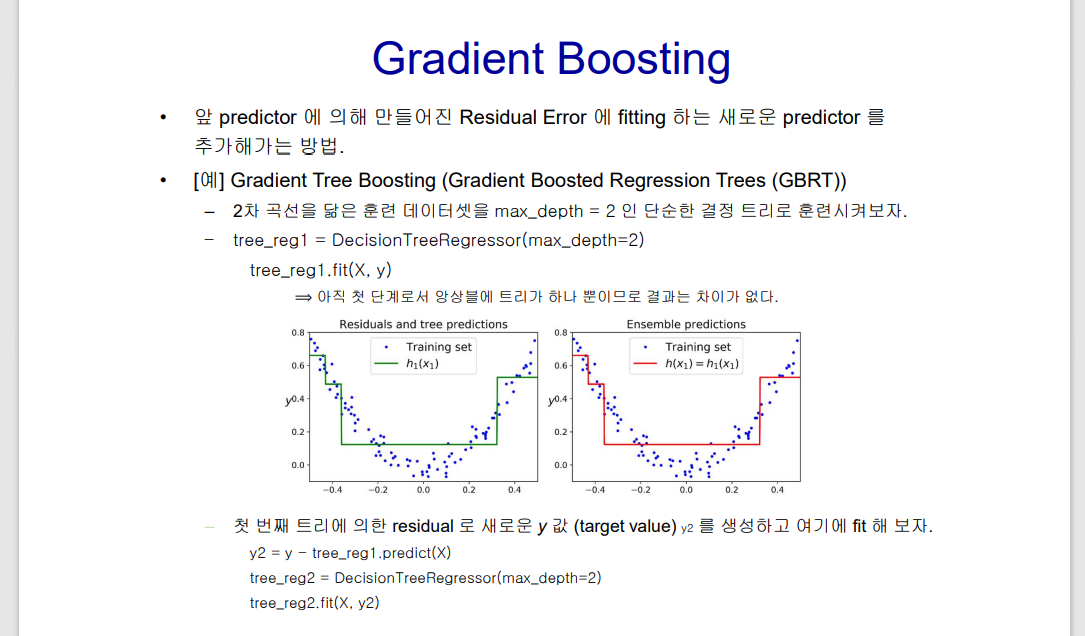
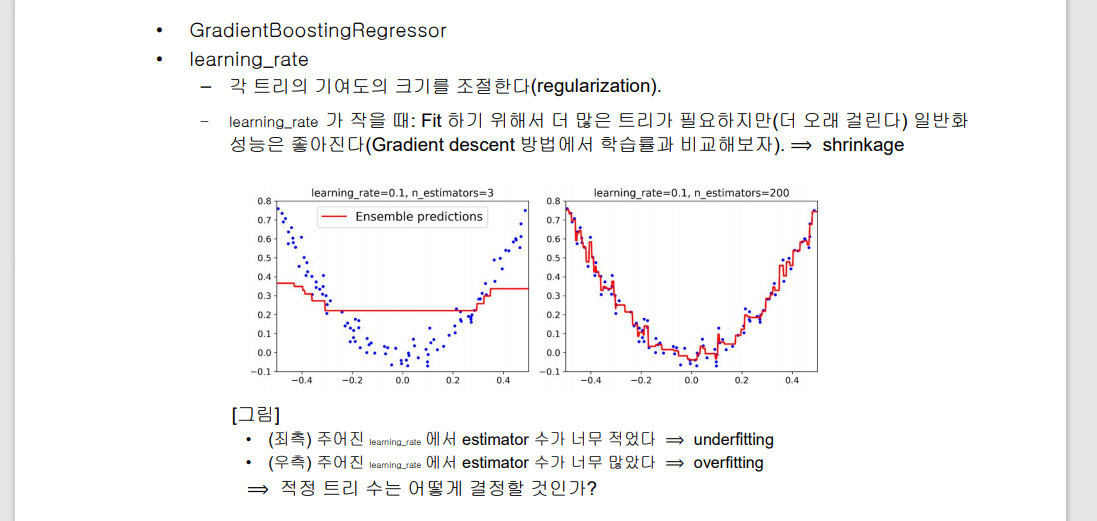

🤔 Regression model (비용 함수: Sum of Squared Error)에서 최상의 결과는 residual sum 이 0 이 되는 것이다.
🤔 Residual 분포의 패턴을 안다면, 그 패턴을 이용해서 model 을 data 에 더 잘 fit 할 수 있지 않을까? 즉, 처음의 regression model 에다가 residual 들에 fit 시킨 별도의 model 을 더하면 더 정확한 예측이 될 것 같다.
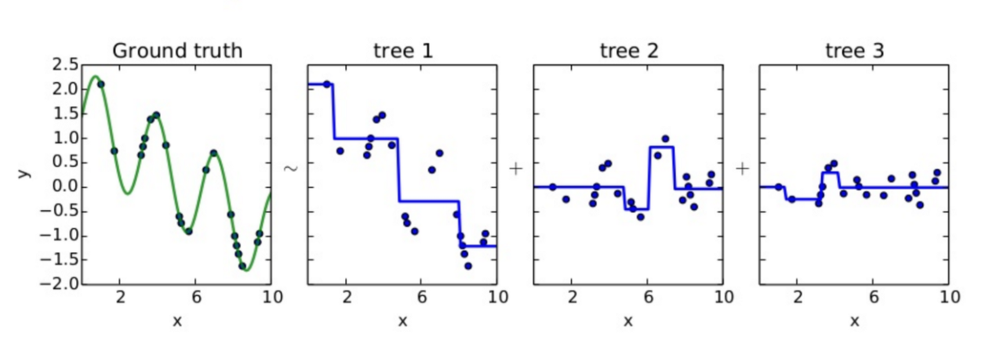
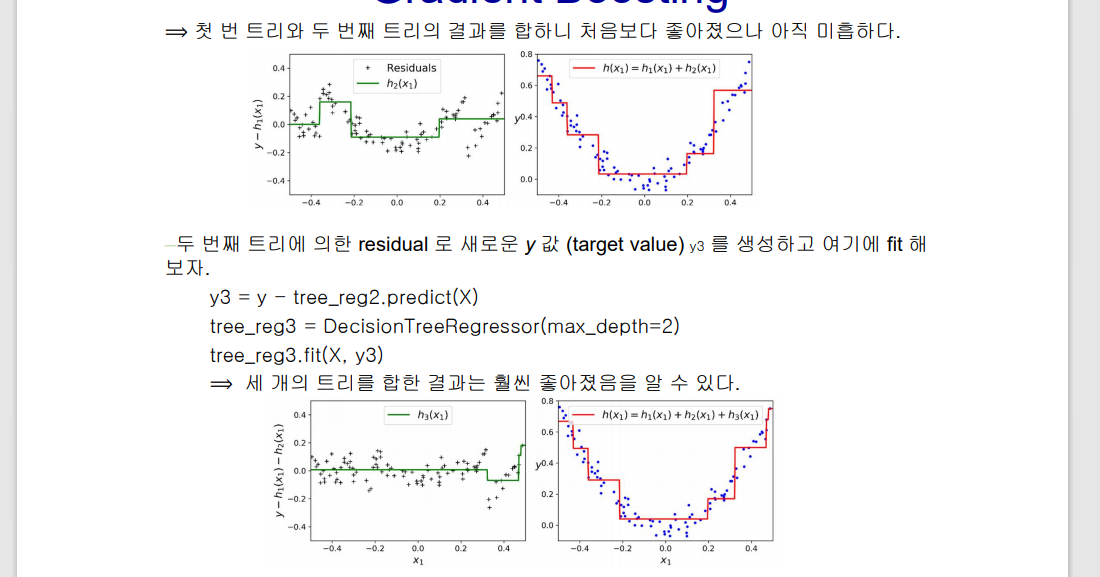
tree 1을 통해 예측하고 남은 잔차를 tree2를 통해 예측하고, 이를 반복함으로서 점점 잔차를 줄여나감. 이 때, 각각의 모델 tree1,2,3 을약한 분류기 (weak learner), 이를 결합한 분류기를 강한 분류기 (strong learner)라고도 함
그래디언트 부스팅(Gradient Boosting)도 아다부스트 처럼 이전 예측기의 오차를 보정하도록 예측기를 순차적으로 추가하지만, 반복마다 샘플의 가중치를 수정하는게 아니라, 이전 예측기가 만든 잔여오차(residual error)에 새로운 예측기를 학습시킨다.
예제 : 키, 좋아하는 색깔, 성별을 기반으로 몸무게를 예측하는 Gradient Boost 모델
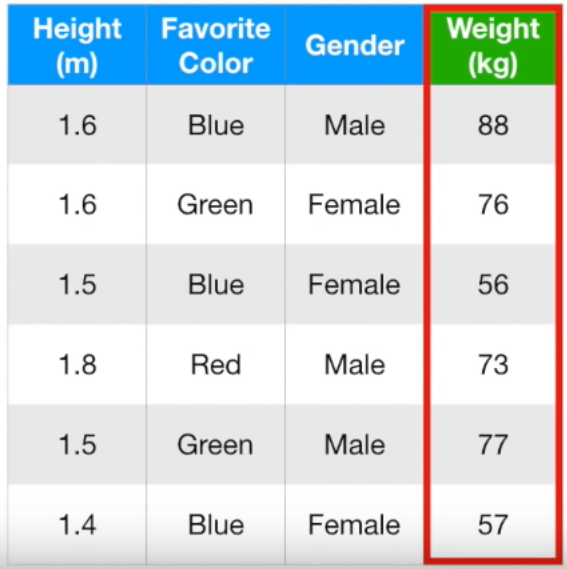
- Gradient Boost는 single leaf부터 시작하며, 그 single leaf 모델이 예측하는 타겟 추정 값은 모든 타겟 값의 평균임.
(88 + 76 + 56 + 73 + 77 + 57) / 6 = 71.2
따라서, single leaf로 몸무게를 예측한다면 모든 사람은 71.2kg이라고 할 것
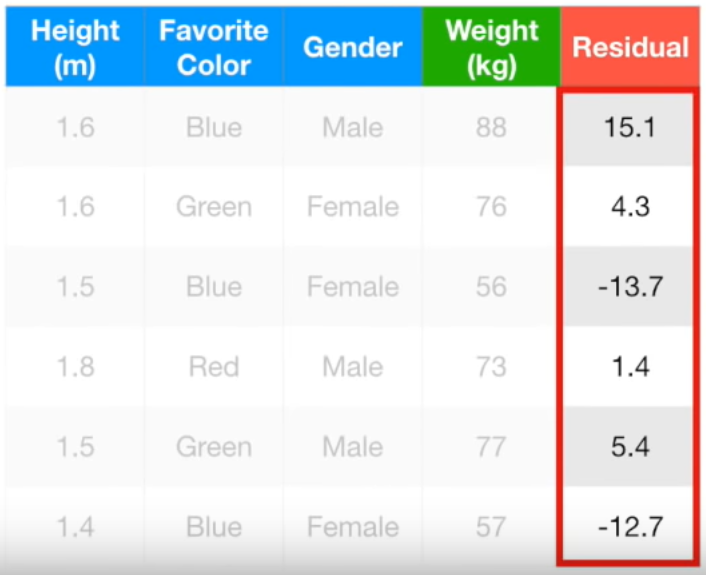
- 첫행의 실제 몸무게 값은 88kg인데 leaf는 71.2kg로 예측. 따라서 차이는 16.8kg (=88kg - 71.2kg)
이를 Pseudo Residual이라고 함. 모든 행의 Pseudo Residual은 아래와 같음.
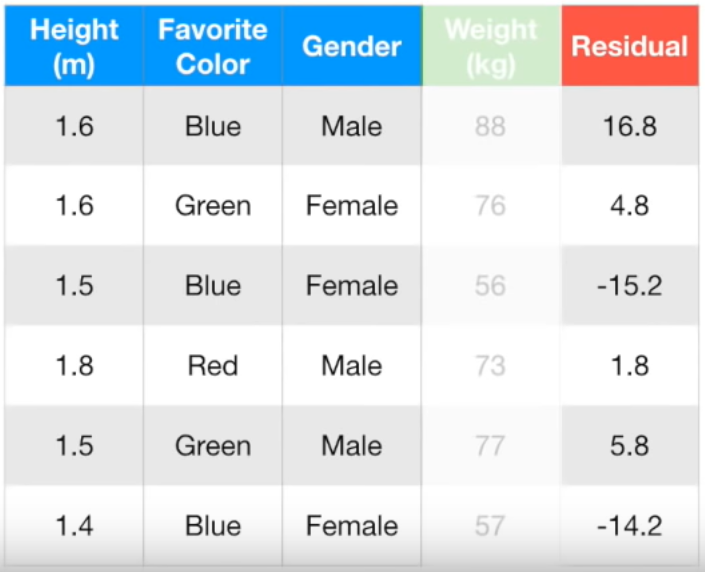
- 키, 좋아하는 색깔, 성별을 통해 Residual을 예측하는 트리를 만들어 보자.
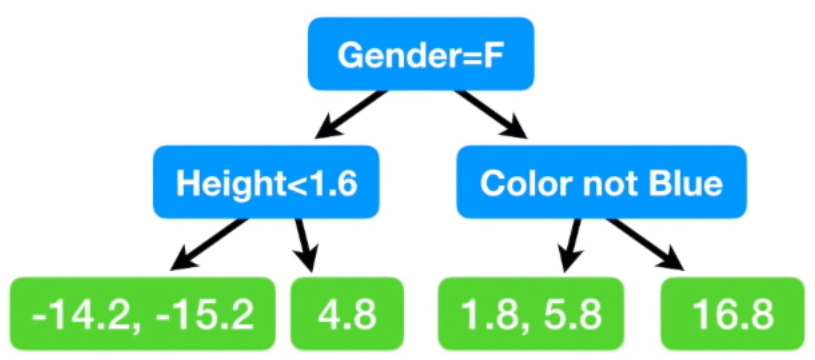
- 맨 처음 노드에서 여자면 왼쪽, 남자면 오른쪽. 왼쪽 노드에서는 Height가 1.6보다 작으면 왼쪽. 오른쪽 노드에서는 blue가 아니면 왼쪽.
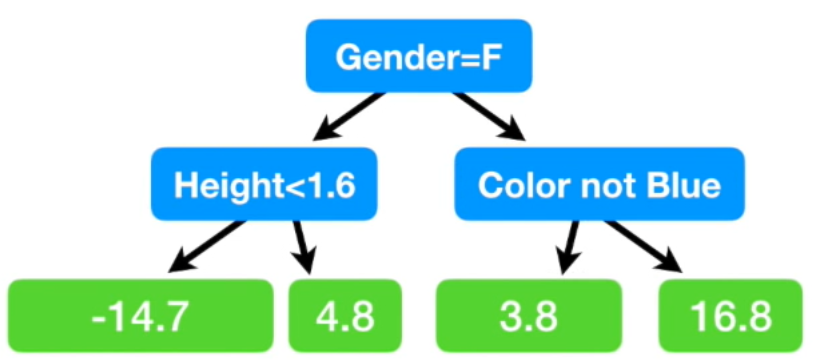
- 노드에 값이 두개일때는 둘의 평균값을 넣어줌
- residual을 업데이트 해줌
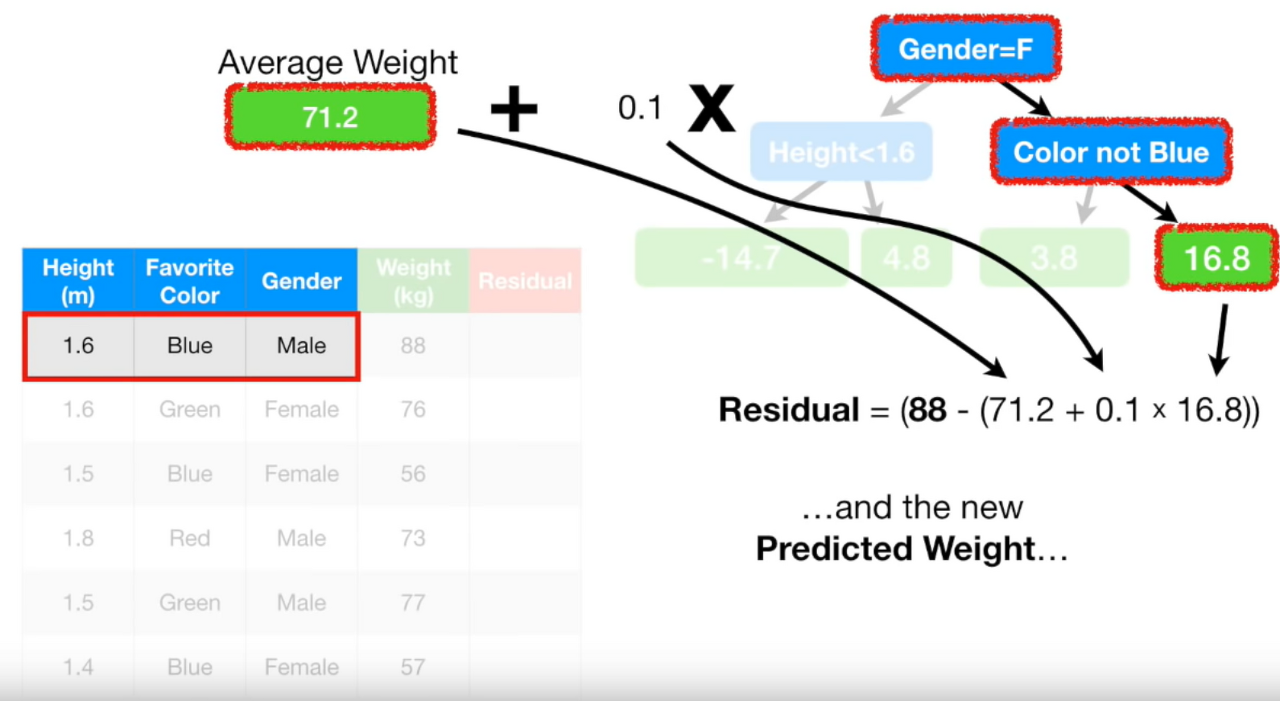
- 예측
지금까지 구한 모델을 통해 키 1.6m에 남자이고, 좋아하는 색깔이 파란색인 사람의 몸무게를 예측

3) XGBoost (eXtreme Gradient Boost)


- 병렬 처리 사용으로 GBM 에서 속도와 정확도 향상
- 과적합(overfitting) 방지가 가능한 변수 규제가 포함되어 있다.
- 계속 훈련하기 때문에 이미 적합화된 모델을 새로운 데이터에 적용이 가능
- CART(Classification And Regression Tree)를 기반으로 한다.
즉, 분류와 회귀가 둘 다 가능하다 - 유연성: 평가함수를 포함하여 다양한 커스텀 최적화 옵션 제공. xgboost
분류기에 다른 알고리즘을 붙여서 앙상블 학습 가능 - 조기 종료(early stopping)을 제공한다.
- 결국 Gradient Boost을 기반으로 한다.
즉, 앙상블 부스팅(ensemble boosting)의 특징인 가중치 부여를 경사하강법(gradient descent)으로 한다. - Greedy algorithm을 사용, 각각의 classifier, M1, M2, M3를 찾고,
분산처리를 사용하여 빠른 속도로 적합한 가중치 (w1, w1, w3)를 찾음
Y = w1 x M1(x) + w2 x M2(x) + w3 x M3(x) + error
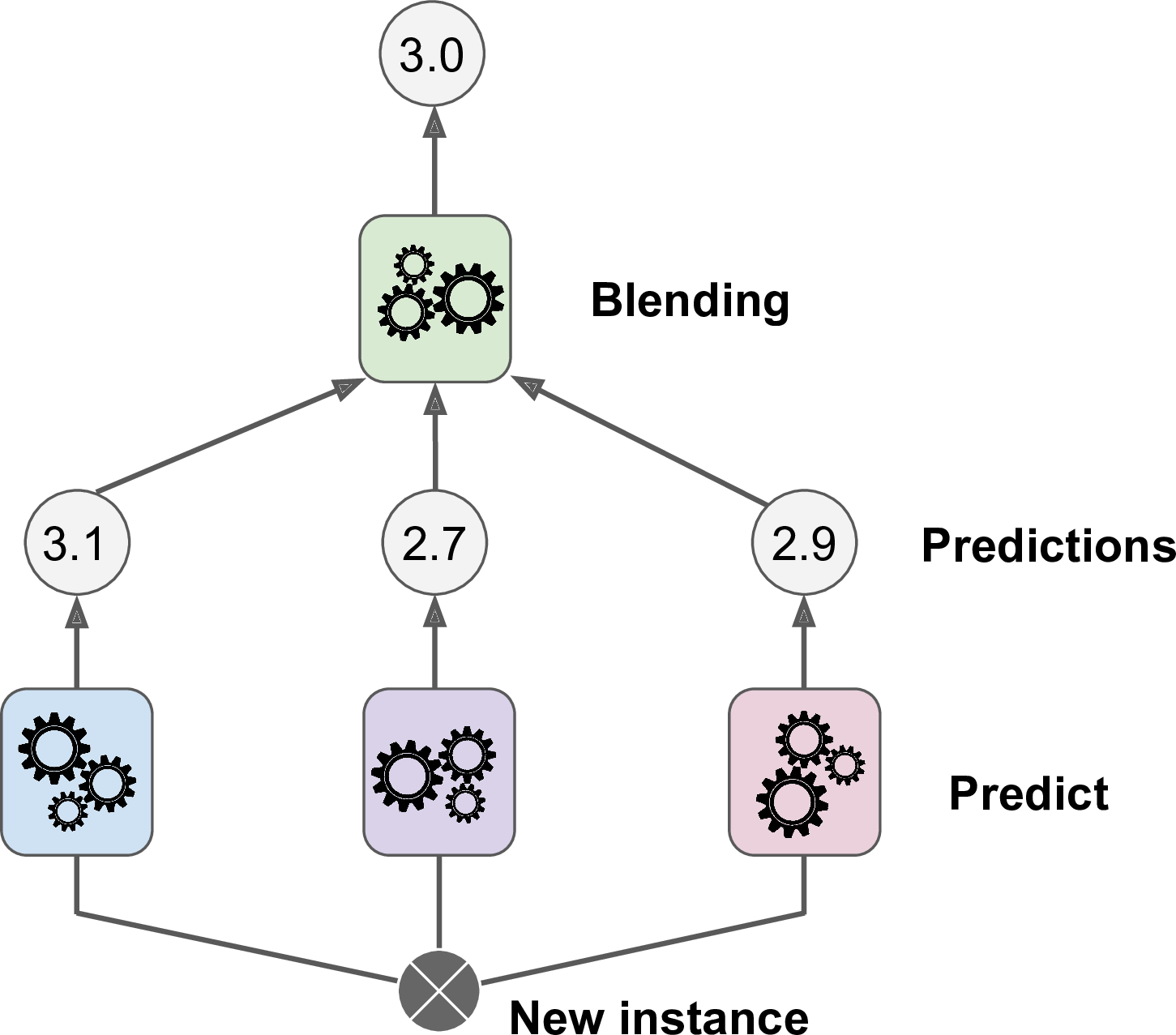
5. Stacking
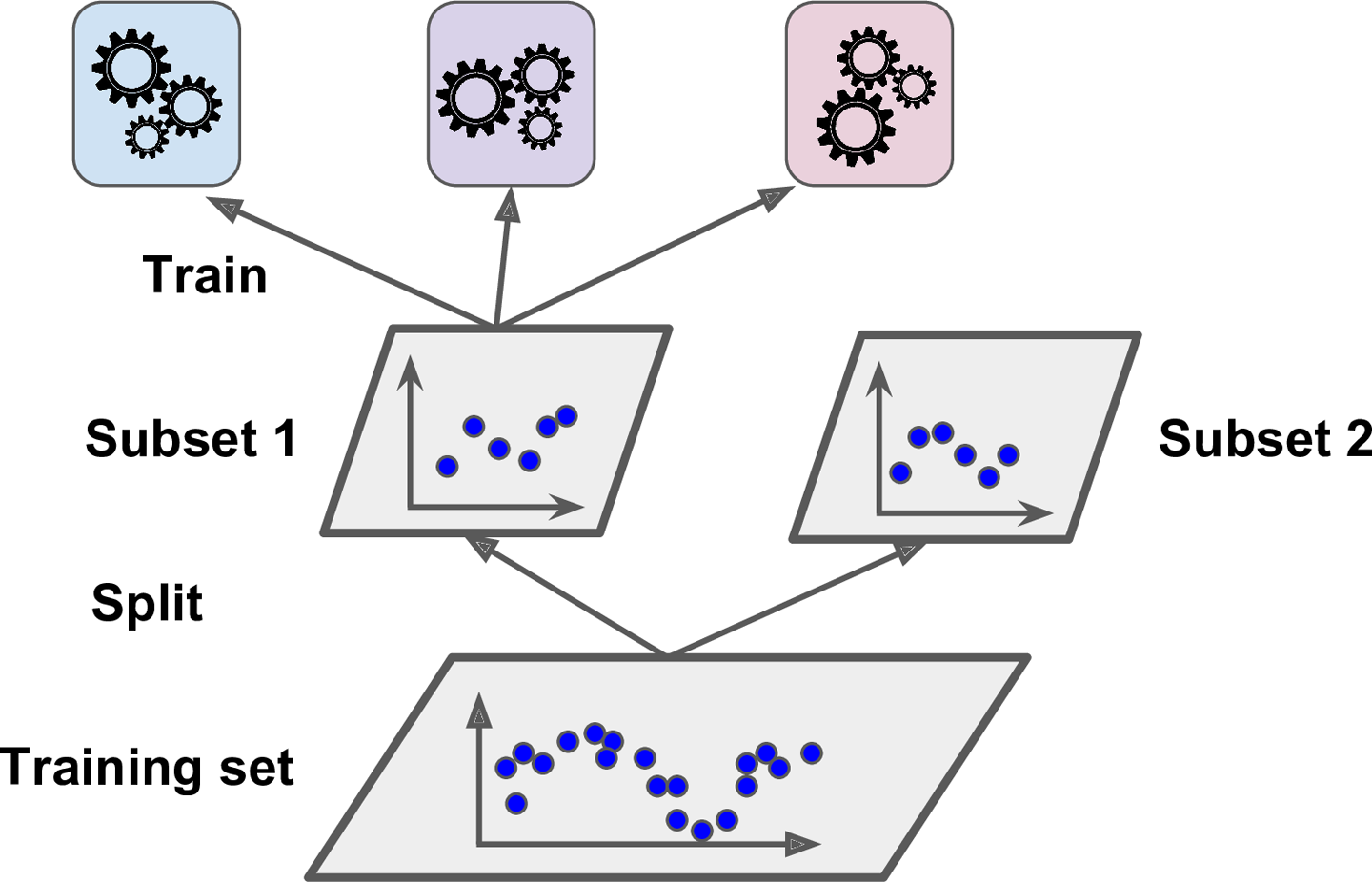
1. 먼저 training set을 2개의 subset으로 나눈다. (hold-out-set)
2. subset1은 첫번째 레이어의 예측기들을 훈련시키는데 사용
3. 훈련된 첫번째 레이어의 예측기로 subset2에 대한 예측을 생성
(subset이지만 훈련에 사용이 안됐으므로 test셋처럼 사용 가능)
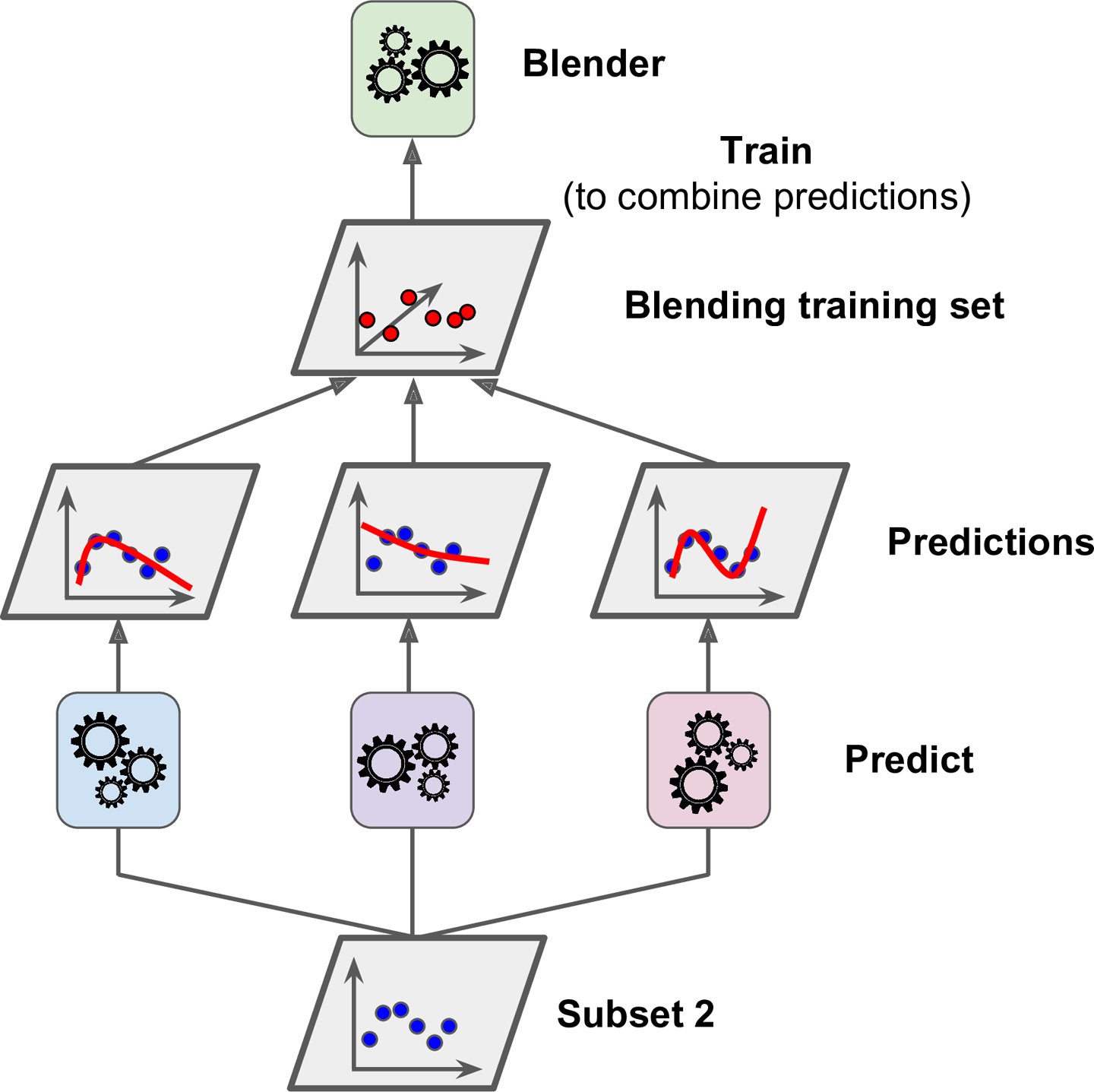
1. 세개의 예측값 생성
2. 타겟값(y)은 그대로 쓰고 앞에서 예측한 3개의 값(y_hat)을 입력 변수로 사용하는 새로운 훈련세트 생성
(즉, 새로운 훈련세트는 3차원이 된다)
3. 블렌더가 새로운 훈련 세트로 학습
(즉, 첫번째 레이어의 예측 3개를 이용해 y를 예측하도록 학습되는 것이다.)
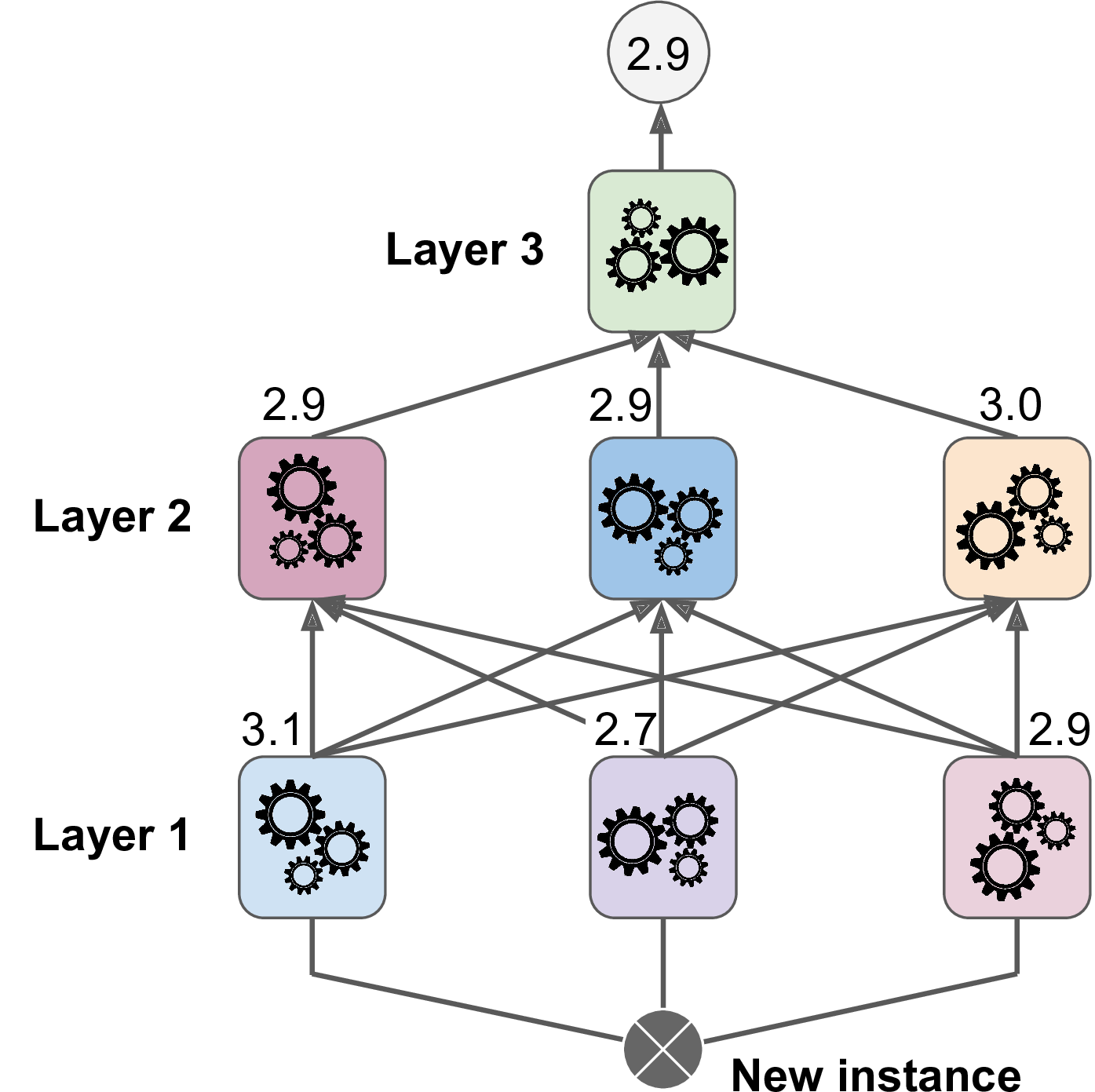
Multilayer stacking
Blender 들 만의 층을 따로 두는 방법
즉, subset1은 첫번째 레이어의 예측기들을 훈련시키고,
subset2로 첫번째 예측기들의 예측을 만들어 블렌더 레이어의 예측기를 위한 훈련세트를 생성하고,
subset3로 두번째 예측기들의 예측을 만들어 세번째 레이어를 훈련시키기 위한 훈련세트를 만드는데 사용된다.