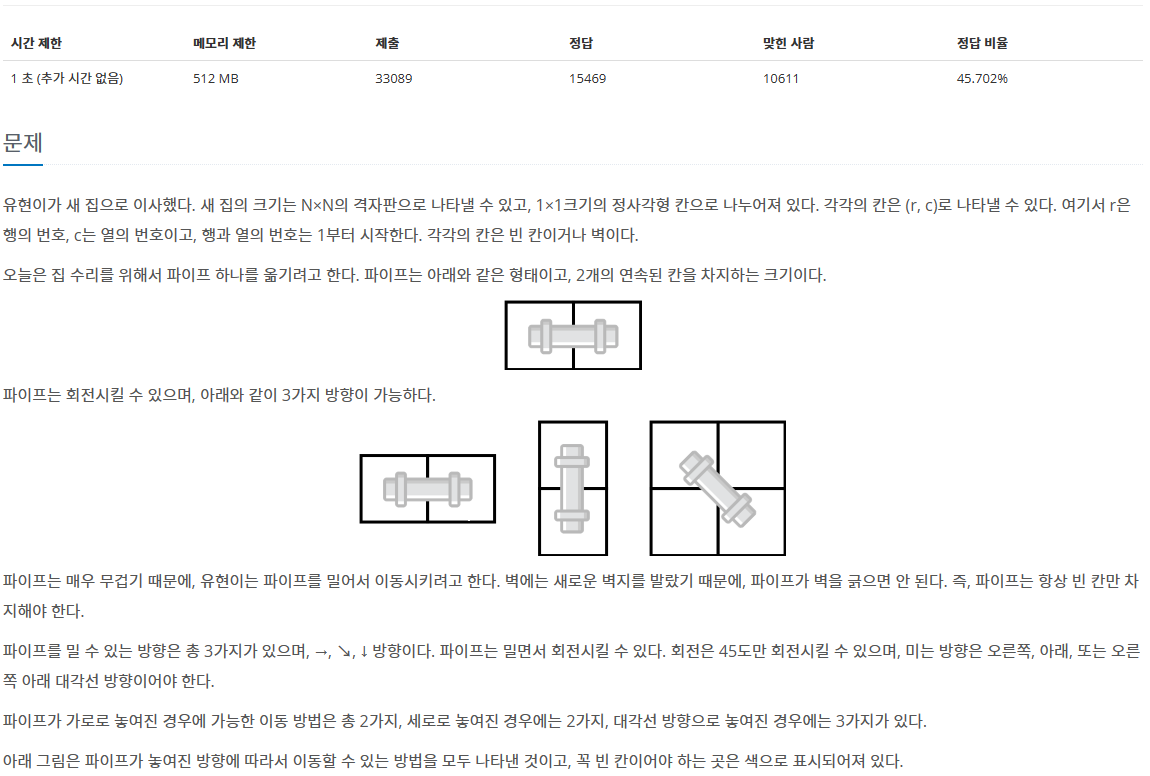
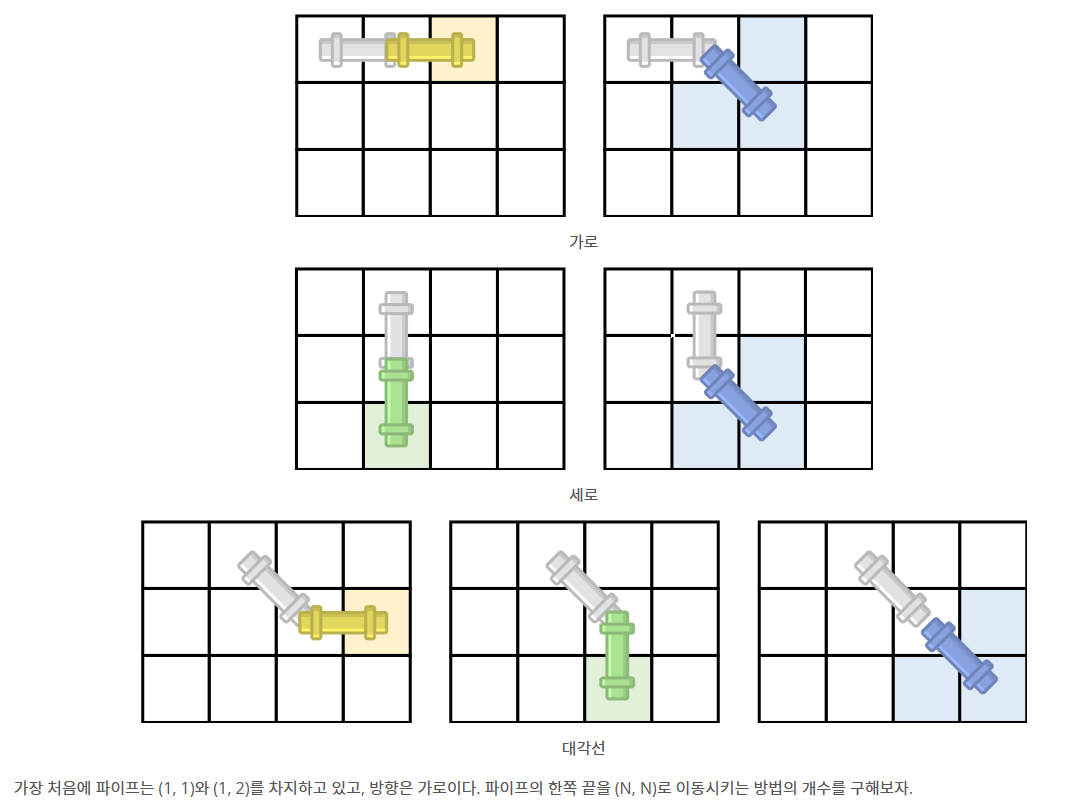
문제

풀이
이 문제는 2가지 방법으로 풀이가 가능하다.
백트래킹
우선 백트래킹으로 문제를 푸는 경우는 파이프를 옮기는 방법의 가지수 마다 그 결과가 (n,n)에 도달하는지를 확인하여 도달한다면 방법의 수 + 1로하여 문제를 해결할 수 있다.
현재 파이프가 어떻게 놓여있냐에 따라 다음 단계로 가는 방법이 달라지며 직관적으로 풀이를 떠올릴 수 있었다.
현재 파이프가 어떻게 놓여있는지를 판단하기 위해 dfs의 매개변수로 현재 파이프가 차지하고 있는 칸 2개를 pair<int, int> 형태로 넘겨주었다. 매개변수로 받아온 파이프의 위치 2개의 x, y 값이 하나라도 일치하면 가로, 세로 방향으로 x,y 값이 일치하는게 없다면 대각선 방향으로 놓여 있다 판단하여 다음으로 넘어가는 경우를 계산했다.
DP
문제에서 요구하는 것이 (n, n)에서 도착하는 방법의 수이다.
이를 구하기 위해서는 아래의 세가지 방법의 수를 모두 합한 것이다.
- (n-1, n),(n, n) 파이프가 세로 방향으로 놓이게 되는 방법의 수
- (n, n-1),(n, n) 파이프가 가로 방향으로 놓이게 되는 방법의 수
- (n-1, n-1),(n, n) 파이프가 대각선으로 놓이게 되는 방법의 수
(n-1, n),(n, n)으로 파이프가 세로로 놓이게 되는 방법의 수를 구하기 위해서는 (n-1, n)에 도착하는 방법의 수 중 세로로 놓일 수 있는 방법의 수를 구해야 한다.
- (n-2, n-1),(n-1, n) 파이프가 대각선으로 놓이게 되는 방법의 수
- (n-2, n),(n-1,n) 파이프가 세로 방향으로 놓이게 되는 방법의 수
(n, n-1),(n,n)으로 파이프가 가로로 놓이게 되는 방법의 수를 구하기 위해서는 (n,n-1)에 도착하는 방법의 수 중 가로로 놓일 수 있는 방법의 수를 구해야 한다.
- (n-1, n-2),(n, n-1) 파이프가 대각선으로 놓이게 되는 방법의 수
- (n, n-2),(n, n-1) 파이프가 가로 방향으로 놓이게 되는 방법의 수
(n-1, n-1),(n,n)으로 파이프가 대각선으로 놓이게 되는 방법의 수를 구하기 위해서는 (n-1,n-1)에 도착하는 방법의 수 중 대각선으로 놓일 수 있는 방법의 수를 구해야 한다.
- (n-2, n-1),(n-1, n-1) 파이프가 세로 방향으로 놓이게 되는 방법의 수
- (n-1, n-2),(n-1, n-1) 파이프가 가로 방향으로 놓이게 되는 방법의 수
- (n-2, n-2),(n-1, n-1) 파이프가 대각선으로 놓이게 되는 방법의 수
이런식으로 (n,n)의 도착 방법을 구하기위해 문제의 초기 상태로 거슬러 올라가는 방법이 필요하다. 파이프가 놓인 방향이 다음 파이프의 방향에 영향을 미치므로 각 위치에서 어떤 방향으로 도착했는지를 구별할 필요가 있다. 따라서 2차원 방 모양의 dp 테이블에서 각 가로, 세로, 대각선을 구별하기 위한 차원을 하나 더 붙여서 3차원 dp 테이블을 만들어준다.
dp[i][j][0], dp[i][j][1], dp[i][j][2]는 각 i열 j행에 도착하는 가로, 세로, 대각선 방향의 파이프 수이다.
위에서 정리한 방법을 점화식으로 나타내어보면
dp[i][j][0] = dp[i][j-1][0] + dp[i][j-1][2]dp[i][j][1] = dp[i-1][j][1] + dp[i-1][j][2]dp[i][j][2] = dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j-1][2]
점화식을 구했으니 초기 값을 구해야 한다.
문제에서 처음 파이프의 위치와 방향을 정해주었다. 문제에서는 (1,1)(1,2)이지만 배열 인덱스로 옮기게 되면 (0,0)(0,1)이다. 이를 통해 dp[0][1][0] = 1로 정의할 수 있다.
또한 dp 테이블의 0행은 모두 가로 방향의 파이프만 위치할 수 있으므로 dp[0][i][0] = dp[0][i-1][0]로 정의된다. (1< i <n)
구한 점화식을 이용하여 2차원 배열을 돌며 해당 칸의 도착 방법의 수를 구할 수 있다. 몇가지 신경써야 할 점들이 있다.
- dp 테이블의 0열과 1열은 어떤 방법으로도 파이프가 도달할 수 없다.
- 해당칸을 정의할때 만약 벽때문에 파이프가 올 수 없는 경우라면 그 칸은 0이된다.
모든 칸을 돌고 n-1, n-1 까지 정의 되었다면 문제에서 요구한 n-1,n-1 칸의 가로, 세로, 대각선 방향의 방법의 수를 모두 합하여 출력하면 된다.
코드
백트래킹 풀이
#include <iostream>
#include <vector>
using namespace std;
int n;
int answer = 0;
vector<vector<bool>> walls;
struct Pos{
int x;
int y;
bool operator==(Pos input){
return input.x == this->x && input.y == this->y;
}
Pos operator+(Pos input){
Pos ret;
ret.x = input.x + this->x;
ret.y = input.y + this->y;
return ret;
}
Pos operator-(Pos input){
Pos ret;
ret.x = this->x - input.x;
ret.y = this->y - input.y;
return ret;
}
};
bool OOB(Pos input){
return input.x < 0 || input.x >= n || input.y < 0 || input.y >= n;
}
bool checkWall(Pos input){
return walls[input.x][input.y];
}
void dfs(pair<Pos, Pos> cur){
if (cur.second.x == n-1 && cur.second.y == n-1) { //if (cur.second == Pos{n, n}) {
answer++;
return;
}
if (cur.first.x == cur.second.x || cur.first.y == cur.second.y){ // 가로, 세로
Pos dir = cur.second - cur.first;
Pos next1 = cur.second + dir;
Pos next2 = cur.second + Pos{1,1};
if (!(OOB(next1) || checkWall(next1))){
dfs({ cur.second, next1 });
}
if ( !( OOB(next2) || checkWall(next2) || checkWall(cur.second + Pos{1,0}) || checkWall(cur.second + Pos{0,1}) ) ){
dfs({ cur.second, next2 });
}
}
else { // 대각선
Pos next1 = cur.second + Pos{1, 0};
Pos next2 = cur.second + Pos{0, 1};
Pos next3 = cur.second + Pos{1, 1};
if (!(OOB(next1) || checkWall(next1))){
dfs({ cur.second, next1 });
}
if (!(OOB(next2) || checkWall(next2))){
dfs({ cur.second, next2 });
}
if ( !( OOB(next3) || checkWall(next3) || checkWall(cur.second + Pos{1,0}) || checkWall(cur.second + Pos{0,1}) )){
dfs({ cur.second, next3 });
}
}
}
int main() {
cin.tie(0);
cin >> n;
walls.assign(n, vector<bool>(n));
for (int i=0; i<n; i++){
for (int j=0; j<n; j++){
bool wall;
cin >> wall;
walls[i][j] = wall;
}
}
dfs({{0,0}, {0,1}});
cout << answer << endl;
return 0;
}DP 풀이
#include <iostream>
#include <vector>
using namespace std;
int main() {
cin.tie(0);
ios_base::sync_with_stdio(false);
int n;
cin >> n;
vector<vector<bool>> walls(n, vector<bool>(n, false));
vector<vector<vector<int>>> dp(n, vector<vector<int>>(n, vector<int>(3, 0))); // 가로, 세로, 대각선
for (int i=0; i<n; i++){
for (int j=0; j<n; j++){
bool wall;
cin >> wall;
walls[i][j] = wall;
}
}
dp[0][1][0] = 1;
for (int i=2; i<n; i++){
if(!walls[0][i])
dp[0][i][0] = dp[0][i-1][0];
}
for (int i=1; i<n; i++){
for (int j=2; j<n; j++){
if (!walls[i][j]){
dp[i][j][0] = dp[i][j-1][0] + dp[i][j-1][2];
dp[i][j][1] = dp[i-1][j][1] + dp[i-1][j][2];
}
if (!(walls[i][j] || walls[i][j-1] || walls[i-1][j])){
dp[i][j][2] = dp[i-1][j-1][0] + dp[i-1][j-1][1] + dp[i-1][j-1][2];
}
// 벽이 있어서 파이프가 지나가지 못하는 구간은 dp 테이블을 0으로 초기화 했기 때문에 굳이 0으로 다시 대입할 필요없다.
}
}
int answer = 0;
for (int i : dp[n-1][n-1]) answer += i;
cout << answer << endl;
return 0;
}
// 현재 칸을 끝으로 하는 가로, 세로, 대각선 파이프의 개수