1. Metric learning task
Metric learning이란 objects들간의 distance function을 배우는 학습 방법론이다. 이때, distance의 정의는 이미지 픽셀 값들의 유사도가 될 수도 있고 각 상황마다 다르게 정의될 가능성이 있다.
추가적으로 언급해보자면, 0과 1 과 같이 직접적인 label이 아닌 간접적인 label이라고 할 수 있는 distance를 가지고 학습을 진행하는 방법론이다. 이러한 이유로 우리는 metric learning을 weak-supervised learning이라 일컫는다. 이러한 metric learning에 어떠한 종류가 있는지를 지금부터 살펴보겠다.
2. learning to rank
해당 task의 데이터로는 아이템들의 list와 물건들의 상대적인 순위인 partial order(전체 순위가 아닌)가 주어진다. 해당 모델이 하고자 하는 바는 아이템들의 순위를 학습 데이터에 존재하는 순위를 반영하여 최대한 가깝게 출력해내는 것이다. 실제 document retrieval(text query가 주어지면 웹페이지들의 순위를 매기기), collaborative filtering, online advertising (유저의 정보를 바탕으로 해당 유저가 특정 광고를 클릭할 확률을 예측하고, 각 회사들이 해당 공간에 광고를 하겠다고 배팅한 가격을 합산하여 광고를 띄어주는 task)분야에서 활용되곤 한다.
2-1. problem formulation
metric learning 분야에서의 문제를 아래와 같이 정의내릴 수 있다.
1) point wise
각 (query - item) pair에 score가 붙여진 데이터를 주고, score를 예측한다. 이는 일반적인 regression이나 classification task라 생각하여 해결 가능한다.
2) pair wise
각 query에 대해서 순위가 붙여진 두 개의 쌍의 데이터를 준다. 모델은 주어진 query를 기반으로 두 개의 아이템 임배딩이 뽑아내고 이렇게 도출된 임배딩을 이용하여 우선순위를 예측한다. objective는 학습데이터 내의 두 아이템 선호 관계가 최대한 보존되도록 설계되어야 한다. 해당 순위를 학습하는 과정에서 모델은 아이템들에 대한 임베딩을 학습하고, 이러한 임베딩이 generalized 되기 때문에 unseen 데이터에서도 효과적으로 순위를 예측하는데 도움이 된다.
3) list wise
후보를 이제 두 개가 아닌 여러 개의 아이템의 순서를 맞추는 것이다. 그냥 계산하면 모든 permutation에 대해, 즉 모든 아이템 조합에 대해 우선순위를 모두 구해야 하기 때문에 계산량이 기하급수적으로 늘어날 수 밖에 없다. 이에 대한 접근법으로 pairwise의 기법을 간접적으로 사용한다.
2-2. evaluation metrics
- Normalized Discounted Cumulative Gain (NDCG)
(relevance가 숫자일때)
(relavance가 실수값일때)
모델이 각 페이지를 1 - p위까지 순서를 매기면, 1위에 있는 것이 정말로 relevance(예를 들어, 실제 유저가 이 페이지를 클릭하였는지)가 있는가를 의미한다. rel이 1이면 실제 클릭을 한 것이고, 아니면 클릭을 하지 않은 것이다. 이때 분모의 i는 예측한 순위인데, 즉 예측한 순위가 높을수록 relevance값이 더 크게 측정되어 반영된다는 말이다. NDCG는, 만약 특정 세션에서 클릭된 페이지가 다른 경우보다 적을 경우 애초에 구해지는 DCG값이 작을 수 밖에 없기 때문에 이를 보완하고자 DCG에 각 세션별 클릭된 페이지 수를 나누어 구하는 metric 값이다.
3. metric learning
3-1. triplet loss
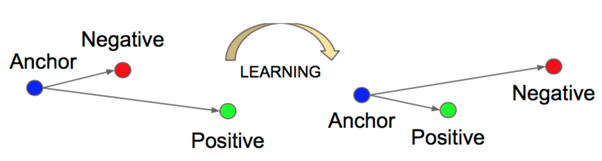
training 데이터가 anchor, positive, negative 총 3가지로 나뉘어질 때, anchor-postive 간의 거리와 anchor-negative간의 거리를 이용하여 학습하는 방법이다. 이때 anchor와 positive간의 거리는 가깝게, negative간의 거리는 멀게끔 학습되어지는 것이 일반적이다.
(hinge loss처럼 양수일 때만 제 loss 값을 갖고 음수면 0으로 바뀐다. 만약 anchor와 postive 간의 거리가 negative간의 거리보다 짧을 경우, 잘 예측했음에도 불구하고 음수가 나오기 때문에 이를 0으로 설정하기 위한 방법이다. 음수 loss로 backprop을 하는 경우 잘 예측했음에도 gradient가 움직이는 경우가 존재하기 때문에, loss는 양수여야 한다.)
는 'margin'의 개념으로, anchor와 positive가 가깝게 설정되더라도 이정도는 더 좁혀야한다는 추가적인 조건을 주기 위해 넣은 요소이다.
아까와 같은 추천시스템의 task에서, positive와 anchor는 유저가 선택한 아이템들에서 선택되고, negative는 유저가 선택하지 않은 임의의 아이템들에서 선택이 된다. 그렇지만 이런 경우 예측이 너무 쉬워지기 때문에 더 예측하기 어려운 pair를 선택할 필요가 존재한다.
이를 위해 negative pair를 잘 선택하기 위한 방법들이 고안되었다. online negative mining이 그 예시이다. hard negative를 뽑아내기 위해, 이를 전체 데이터셋에서가 아닌 mini batch에서 뽑아내는 방법을 선택했다. 일단 mini batch에서 데이터를 뽑아냈기 때문에 컴퓨팅적으로 효율적이고, 또한 batch의 하나의 positive 데이터가 batch 내의 모든 negative 데이터와 멀어지도록 학습이 되어지기 때문에 성능이 더 높아질 수 밖에 없다. 그래서 batch 사이즈가 더 커야 한다는 요구사항이 존재한다.
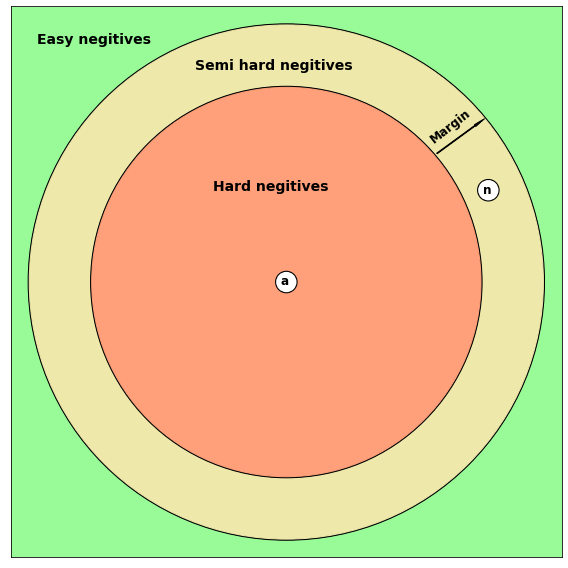
이후에는 semi hard negative mining 개념도 등장하였다. 우선 개념은 아래와 같다.
-
Easy negatives: d(a,p)+margin < d(a,n) 이미 충분히 거리가 먼 negative의 경우
-
Hard negatives: d(a,n) < d(a,p) 거리가 positive보다 가까워 명백하게 위해되는 경우
-
Semi-hard triplets: d(a,p) < d(a,n) < d(a,p) + margin 거리가 애매하게 먼 경우
만일 그냥 hard negative만을 뽑게 되는 경우 문제가 발생할 수 있다. 에서 모델의 이상적인 학습방향은 앵커와 negative간의 거리를 멀게 만드는 것이지만, alpha가 굉장히 작은 값이기 때문에 모델이 그냥 f(x)에 대한 결과값이 모두 0으로 출력되게끔 할 수 있다. 이러한 경우 학습이 제대로 이뤄지지 않는다. 그래서, 현재의 anchor - negative distance가 anchor - positive distance를 아슬아슬하게 넘는 negative를 선택하여 해당 경우들을 잘 학습시키는 것이 중요하다. 추가적으로 alpha값들을 잘 설정하는 것도 중요하다.
실제 이를 활용하는 분야로는 FaceNet, CDML 등이 존재한다. 그 중 collaborative deep metric learning에 대해 살펴보자.
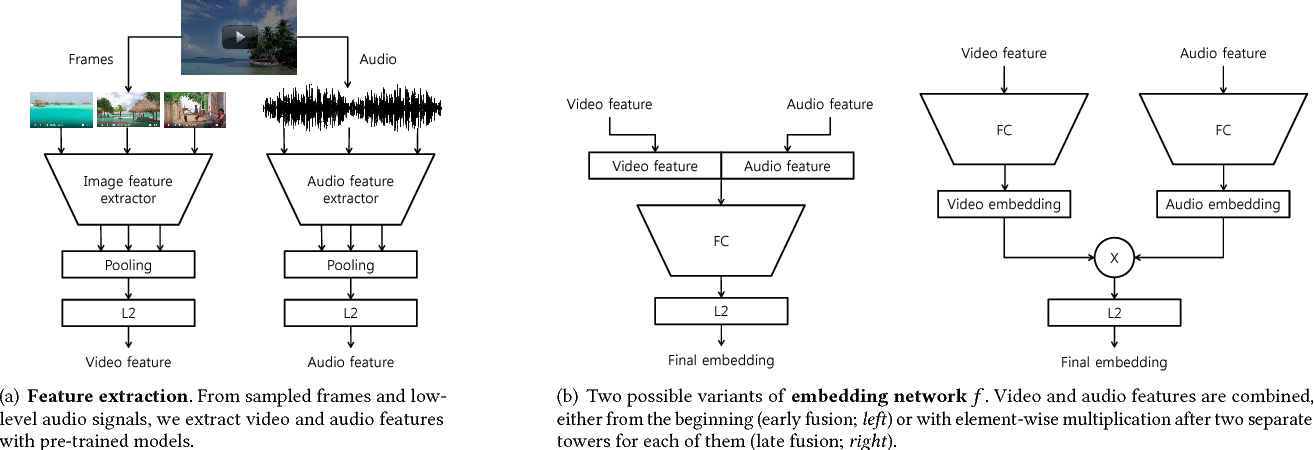
프레임과 오디오의 피쳐를 뽑아 anchor와 negative는 멀도록, anchor와 positive는 가깝도록 임베딩 모델 학습을 진행한다. 이때 특정 비디오를 보고 선택한 비디오들을 연관이 있다고 생각하여 postive pair라 여기고 인근 노드에 배치한다. 아닌 것들은 거리가 먼 노드에 배치함으로써 비디오 연결 관계를 그래프 형식으로 빌드하고 이를 통해 각 데이터셋을 마련한다. 이를 통해 비디오 임베딩을 뽑아내고 Nearest neighbor search, user modeling, classifier 등 다양한 곳에서 활용 가능하다. 한계점은 negative pair를 효과적으로 뽑아내기 위해서 batch size를 크게 잡아야 한다는 점이 있다.
3-2. Contrastive learning
0) pairwise loss function
Input examples pair 에 대해, 두 데이터가 유사할 때 ground truth distance y는 0, 유사하지 않을 때는 1로 생각한다. 어떤 대상이 유사할 땐 가깝게, 유사하지 않은 대상은 멀게 배치되게끔 학습시키기 위해 아래와 같은 loss값이 설계되었다.
이때,
이다.
해당 loss값의 예시는 아래와 같다. 실제 유사한 데이터인 경우(Y=0)는 , 반대의 경우는 을 loss값으로 채택하는 것이다.
다만 이러한 loss function에는 어떠한 문제가 존재한다.
- normalization problem
우리는 classification task에서 어떠한 값을 예측을 할 때, 주로 softmax 함수를 이용하곤 한다.
이때, softmax값으로 하나 클래스에 대한 확률을 계산하려고 할때, 모든 클래스에 대한 score 점수도 모두 구해야한다. 즉, 분류할 수 있는 클래스의 수가 많을수록 더 많은 계산이 요구된다는 것이다. 또한 매번 특정 클래스를 도출해내기 위한 모든 파라미터들을 업데이트를, 그리고 이 과정을 모든 클래스에 대해 적용한다는 것이다.
그래서, 어느정도 학습이 완료된 후에는 negative를 다 쓰지말고, softmax 분모의 에서 일부만 랜덤으로 선택하여 쓰자는 아이디어가 등장하였다. 이를 negative sampling이라고 한다.
1) SimCLR
simCLR의 구조는 아래와 같다. Data Augmentation을 통해 하나의 이미지를 여러 유사한 이미지로 만든 후 인코더에 집어넣는다. 이렇게 만들어진 1차적인 임베딩을 projection을 시켜 2차 임베딩을 뽑는다. 같은 이미지로부터 나온 2차 임베딩들은 유사하도록 학습이 된다(positive pair). 그 이외 negative pair로는 batch에 있는 나머지 이미지들을 사용한다.

아래는 simCLR의 알고리즘이다.

여기서 loss는 분자에 유사한 이미지 pair 의 점수, 분모는 자기자신을 제외한 나머지 이미지들, 즉 유사하지 않는 pair들의 점수 가 오게 된다.
논문에서는 이미지들에 적용되는 augmentation에 따라, 그리고 이 augmentation의 조합에 따라 성능이 다르게 나온다고 한다. 다만 마찬가지로, simCLR 또한 negative pair가 많을수록, 즉 batch size가 커야지만 학습이 잘 이루어진다는 단점이 존재해서, 이러한 단점을 보완한 MoCo라는 후속 논문도 등장하였는데 이는 추후 다른 글로 정리해보도록 하겠다.
2) NCE: Noise Contrastive Estimator
해당 모델에서는 softmax 대신에 binary classifier를 사용하였다. 두 개의 input word가 어울릴 수 있냐 없냐는 판단하는 것이다. True pair와 Fake pair를 만들어서, true인지 pair인지 예측하는 방법이다.
만약 training data가 개까지 있다고 가정해보자. 이때 이 데이터들이 샘플링되었다고 가정되는 이라는 확률 분포가 존재한다고 생각하자. 우리는 이 을 최적화하는 것이 목표이다. () 원래는 지금까지 모든 클래스에 대한 를 최적화하는 것이 목표였다. NCE는 여기서 fake인 probability distribution도 도입한다. 그리고 N개 를 랜덤하게 sampling 한다. 이때 과 에서 나온 데이터들이 구분되도록 학습을 한다. 마치 가짜인지 진짜인지 구분하는 binary classification 문제가 된 것이다.
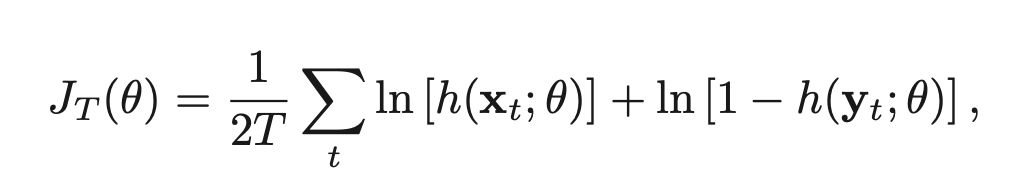
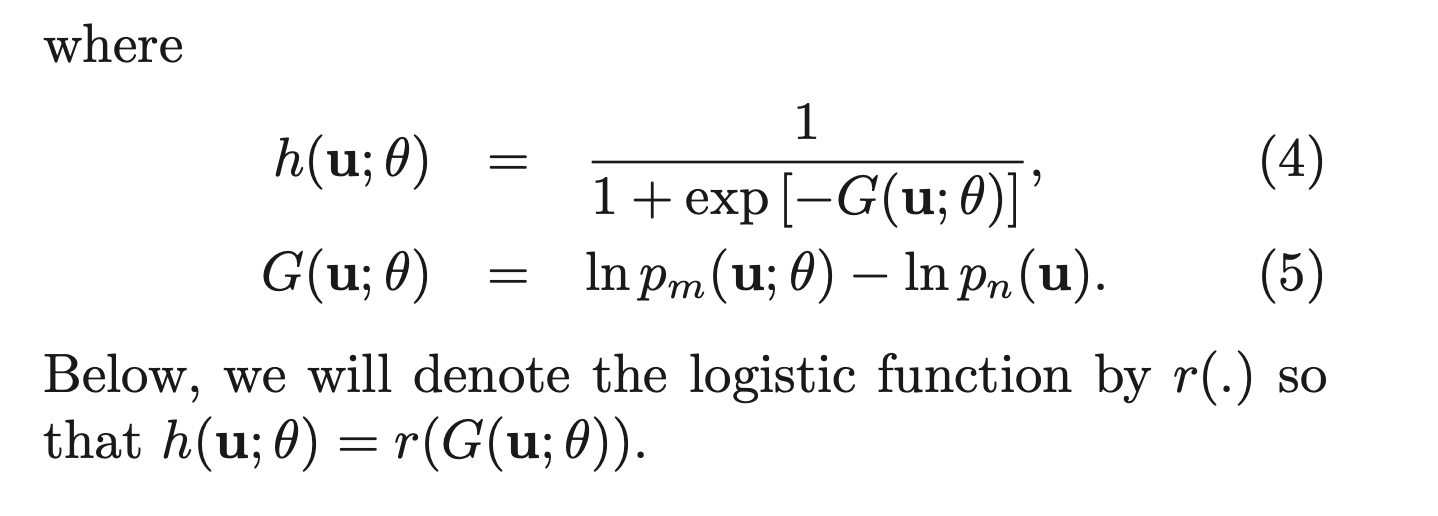
추후 자주 등장할 InfoNCE에서도 사용되는 개념이므로 잘 이해하고 넘어가야 한다.. 이 부분도 논문을 참고하여 좀 더 명확히 이해를 해보자
아래의 강의를 참고하여 작성하였습니다. https://www.youtube.com/watch?v=cv_iOJ_OaUM&list=PL0E_1UqNACXDTwuxUzCl5AeEjXBfWxCwc&index=18
