[논문 리뷰] Learning to Compare: Relation Network for Few-Shot Learning

1. introduction

거대 데이터로 학습된 모델은 이전에는 존재하지 않았던 새로운 카테고리를 분류하고자 할 때, 대용량의 데이터로 학습해야 하는 경우가 존재한다. 적은 데이터로는 fine-tuning을 진행시키기 힘들고, 증강 기법은 overfitting의 위험성이 존재하기 때문이다. 이때 Few shot learning은 적은 라벨 데이터로 새로운 카테고리를 잘 학습하도록 한다. 현 meta learning 접근 방법으로는 initial condition, embedding, optimisation 전략을 선택함으로써 최적화하는 방법을 택하고 있다.

그러나 이러한 few-shot learning도 문제점이 존재한다. network weight을 업데이트하지 못하는 경우도 존재하고, 데이터가 불충분할 경우 gradient descending이 어려워지기 때문이다. 이에 대한 해결책으로 저자는 one-shot learning에 쓰일 수 있는, 효율적인 metric을 제공한다. 이러한 metric은 이미지들 사이에 관계를 비교할 수 있도록 transferable한, 즉 변할 수 있는 deep metric을 제공한다. 이전에 유클리디안 distance와 같은 fixed metric을 사용하는 것과는 다른 양상이다. 또한, deeper solution을 위해 inductive bias를 도입했다고 한다.(임베딩과 relation 모듈간의 여러 비선형적인 관계를 도입하는 것.) 여기서 inductive bias의 개념을 확실히 짚고 넘어갈 필요가 있어서 아래의 글을 첨부한다.

Inductive bias란 무엇일까?

Inductive bias에 대해 간단하게 설명하자면, 기존 모델의 오차에 bias와 variance가 동시에 등장하는 것을 알고 있을 것이다. 이때 bias란, 주어진 학습데이터에 잘못된 가정을 하여 발생한 오차에 해당한다. 근데bias가 낮다고 하여 무조건 좋은 모델은 아니다. 모델이 그럴듯하게 bias가 낮게 모델을 학습시켰다 하더라고, 주어진 데이터가 아닌 새로운 데이터에 대해서는 오차가 높게 발생할 수도 있기 때문이다. 이를 보완하기 위해 등장한 개념이 바로 inductive bias이다. 주어지지 않은 입력에 대해서도 출력을 잘 예측할 수 있도록, 일반화의 성능을 높일 수 있도록 만일의 상황에 대해 추가적인 가정을 두는 것이라고 생각하면 된다. (inductive bias는 보지 못한 데이터에 대해서는 귀납적 추론이 가능하도록 하는 알고리즘을 가지고 있는 가정의 집합)
이 가정들 중 relational 가정에 대해 설명을 하자면, 입력 요소와 출력 요소의 relation 관계가 있음을 가정하는 것이다. CNN을 예시를 들어보겠다. 기존의 fully connected layer는 각 입력 요소가 모든 출력요소와 관계가 있음을 가정하고 모두 연결을 시킨다. 이미지로 예시를 들면 하나의 픽셀 값 하나하나가 출력에 연관이 있다고 생각하는 것이다. 반면 CNN은 특정 출력을 내뱉기 위해서는 globally하게 모든 이미지 파트를 집중할 필요가 없고, 이미지의 일부만 보고 판단할 수 있다고 가정하여 locality를 반영한 모델이다. 즉 입력들간의 관계가 존재하고, 이러한 관계를 반영할 수 있을 때 좋은 출력이 나온다는 것이다. 이때 이 locality 가정을 relational 가정이라고 생각하면 된다.

저자는 최종적으로 two branch relation network를 제안하였고, 이러한 network는 query images와 few-shot labeled sample images의 비교를 통해 학습을 진행한다. 자세한 과정은 아래와 같다. 1) embedding module이 query과 학습 이미지의 representation을 생성한다. 2) 이러한 임베딩은 카테고리 소속 여부를 판단하는 relation module을 통해 비교된다.

2. Related work

기존의 few-shot learning 기법은 적은 데이터를 fine tuning하면 생기는 overfitting 문제를 피하면서 meta learning & learning to learn 전략을 통해 transferrable knowledge를 효과적으로 추출한다. 뒤에서는 이러한 기법에 대해 소개하도록 하겠다.

2-1. Learning to Fine-Tune

MAML approach은 fine-tuning에 적절한 initial condition을 배우는 것을 목표로 한다. (sparse data가 주어졌음에도, 적은 gradient 업데이트 단계를 통해 적절한 weight configuration을 찾는 등) 많은 task training set에서 다양한 target problem이 샘플링 되고, base model은 각각을 해결하기 위해 fine-tuning을 진행한다. 그리고 few-shot optimisation approach 또한 optimizer와 좋은 초기 condition을 학습하려한다. 다만 이러한 접근법 모두 target problem에 fine tuning을 진행해야한다는 문제점이 존재한다. 반면 저자의 접근법은 target problem에 모델 업데이트가 필요없는, feed foward 방식을 통해 해결하려고 한다.

2-2. RNN Memory Based

다른 방법으로는 RNN with memory 접근법이 존재한다. 새로운 데이터를 memory에 저장된 정보와 비교를 함으로써 분류하는 방법에 해당한다. 다만 이러한 접근법도 데이터를 잊지 않고, 과거 모든 정보를 저장하려고 한다는 문제점이 존재한다. 저자의 접근은 이러한 복잡성을 피하기 위해 간단한 feed-foward CNN을 제공한다.

2-3. Embedding and Metric Learning Approaches (보충 필요)

위의 방법들은 학습 시 약간의 복잡성을 수반한다. 다른 방법으로는, query와 이미지를 feed forward 방법으로 분류하는, projection function을 학습시키는 것을 목표로 한다. 하나의 방법은 sample set 관점에서 feed foward classifer의 가중치를 parameterise하는 것이다. metric based 접근법은 projection function을 학습시킨다. 이를 통해 이미지들이 임베딩 될 때, 이미지들은 쉽게 인식되어질 수 있따. 이때 meta-learned transferrable knowledge는 projection function이고, target problem은 simple feed-forward computation이다.

2-4. Zero-shot Learning

few-shot learning과 다르게 zero-shot learning은 몇 샘플 이미지 대신 카테고리의 설명을 입력으로 사용하여 학습을 진행한다. ZSL을 적용시 이미지와 카테고리 임베딩을 정렬하고, 이미지와 카테고리 임베딩 쌍이 일치하는지 예측하여 인식하는 방법과 관련이 있다. 이전 방법과 유사하게 이미지와 카테고리 임베딩을 결합한 후 fixed metric이나 linear classifier를 적용한다. 반면, 저자는 non-linear metric을 사용한다는 점에서 차이점이 존재한다.

3. Methodology

3-1. problem definition

본격적으로 문제 정의를 해보겠다. 총 세가지의 데이터셋을 우선 만들어야 한다. 1) training set 2) support set 3) testing set이다. 이때 support set과 test set은 동일한 label space를 공유하고, training set은 이러한 label space와는 동떨어진 별개의 label space를 지니고 있다. 그리고 각 support set이 c개의 classes에 대해 k개의 label 데이터를 지니고 있다면 이것을 C-way K-shot 문제라고 부른다. 만약 support set를 지니고 있다면, 우리는 test set의 입력데이터을 분류할 수 있는 classifer를 학습시킬 수 있다. 다만, support set에 라벨 데이터가 부족하다면, 이 분류기의 성능은 만족스럽지 못할 것이다. 그래서 저자는 meta learning을 학습데이터에도 적용하려 한다.

학습데이터를 효과적으로 사용하는 방법은, 바로 episode based learning을 통해 few shot learning의 방법을 모방하는 것이다. 각 학습 iteration에서, episode는 randomly하게 C개의 classes를 고르고, 각 C개의 클래스에 대해 K개의 label sample을 뽑는다. 이를 sample set이라 칭하겠다. 그리고 이러한 C 클래스의 sample에서 남은 부분을 Query set이라 칭하고, 각각을 아래와 같이 표기를 하겠다.
$S=\{(x_i,y_i)\}^m_{i=1} \quad ,(m=K*C)$
$Q=\{(x_j,y_j)\}^n_{j=1}$
이러한 sample,query set은 test time에 support, test set처럼 작용한다. 이렇게 학습된 모델은 추후 support set을 통해서 fine-tuning되어질 수 있다. 저자는 이러한 episode 방식의 학습 전략을 선택하였다. 논문에서는 one-shot, five-shot, zero-shot 각각을 테스팅하였다.

3-2. model

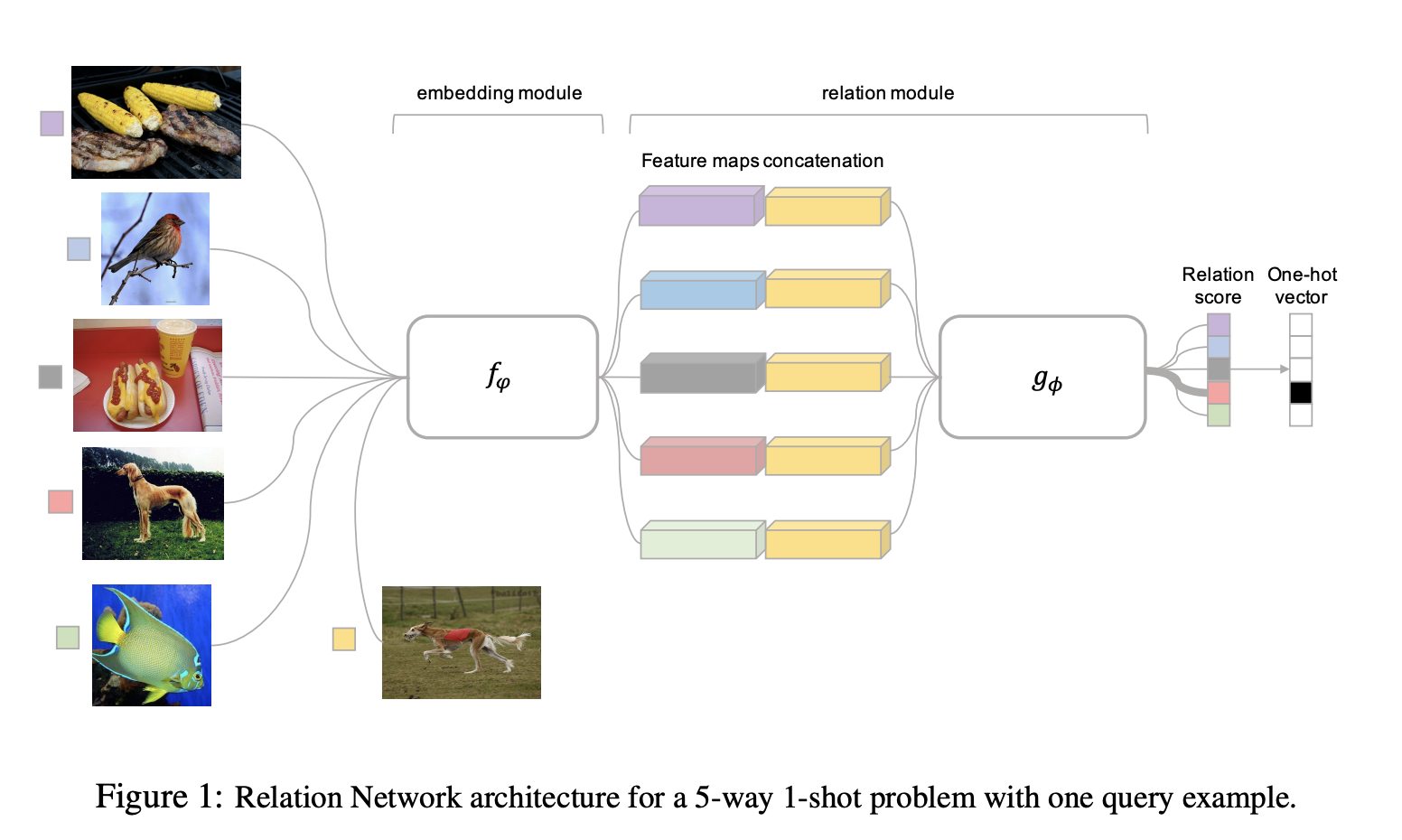
One-Shot

Relational Network는 총 2가지 모듈로 구성되어져 있다. 첫번째로는 embedding module $f_\phi$, 두번째로는 relation module $g_\phi$로 구성되어져 있다. Query set $x_i$의 sample과 sample set의 sample$x_j$은 임베딩 모듈인 $f_\phi$에 활용되게 되고, 이는 $f_\phi(x_i)$와 $f_\phi(x_j)$를 생성한다. 그리고 이러한 feature map은 operator $C(f_\phi(x_i),f_\phi(x_j))$와 결합된다. 이때, $C(.,.)$은 feature map의 concatenation에 해당이 된다. 이렇게 결합된 feature map은 relation module $g_\phi$에 들어가게 된다. 이는 $x_i$와 $x_j$ 간의 유사성을 0-1사이 숫자로 표현한다. 이를 relation score라고 한다. 그러므로, C-way one shot setting에서는, 하나의 쿼리 이미지에 대해 training sample set인 $x_i$간의 관계를 구하여 C개의 relation score인 r_{i,j}를 생성한다.

$r_{i,j}=g_\phi(C(f_\phi(x_i),f_\phi(x_j)))\quad, i=1,2,...C$

k-shot

• 각 클래스에 대해 참고하는 이미지가 k개일 때
  만약 K>1인 경우, K-shot problem에서는 각 샘플들의 embedding module의 ouputs를 element-wise sum을 구한다. 이 feature map을 query set feature map과 결합한다. one-shot과 동일하게 C개의 score가 등장한다.

Objective function

우리는 모델을 학습시키기 위해 (relation score를 regressing 하기 위해) MSE를 사용한다. matched pair에 관해서는 1, mismatched pair에 한해서는 0으로 예측하려 한다.

$\phi, \Phi \leftarrow argmin \sum^m_{i=1}\sum^n_{j=1}(r_{i,j}-1(y_i==y_j))^2$

MSE를 고른 이유는, 분류 문제임에도 relation-score를 예측해야하는 회귀문제기 때문에 이를 사용했다.

3-3. zero-shot learning

기존에는 support set에서 k 개의 sample 뽑아냈다면, zero shot에서는 대신 각 클래스에 대한 semantic class embedding vector인 $v_c$를 활용한다. 즉 이미지 대신 다른 modality인 $v_c$를 사용한다는 말이다. 대신 $v_c$를 입력으로 넣을 $f_{\phi_2}$r가 추가로 필요로 되어진다. 그 다음 relation module에 입력으로 넣는 과정 모두 동일한다. objective function 또한 동일하다.
$r_{i,j}=g_\phi(C(f_{\phi 1}(v_c),f_{\phi 2}(x_j)))\quad, i=1,2,...C$

3-4. Network Architecture

Few shot learning Network

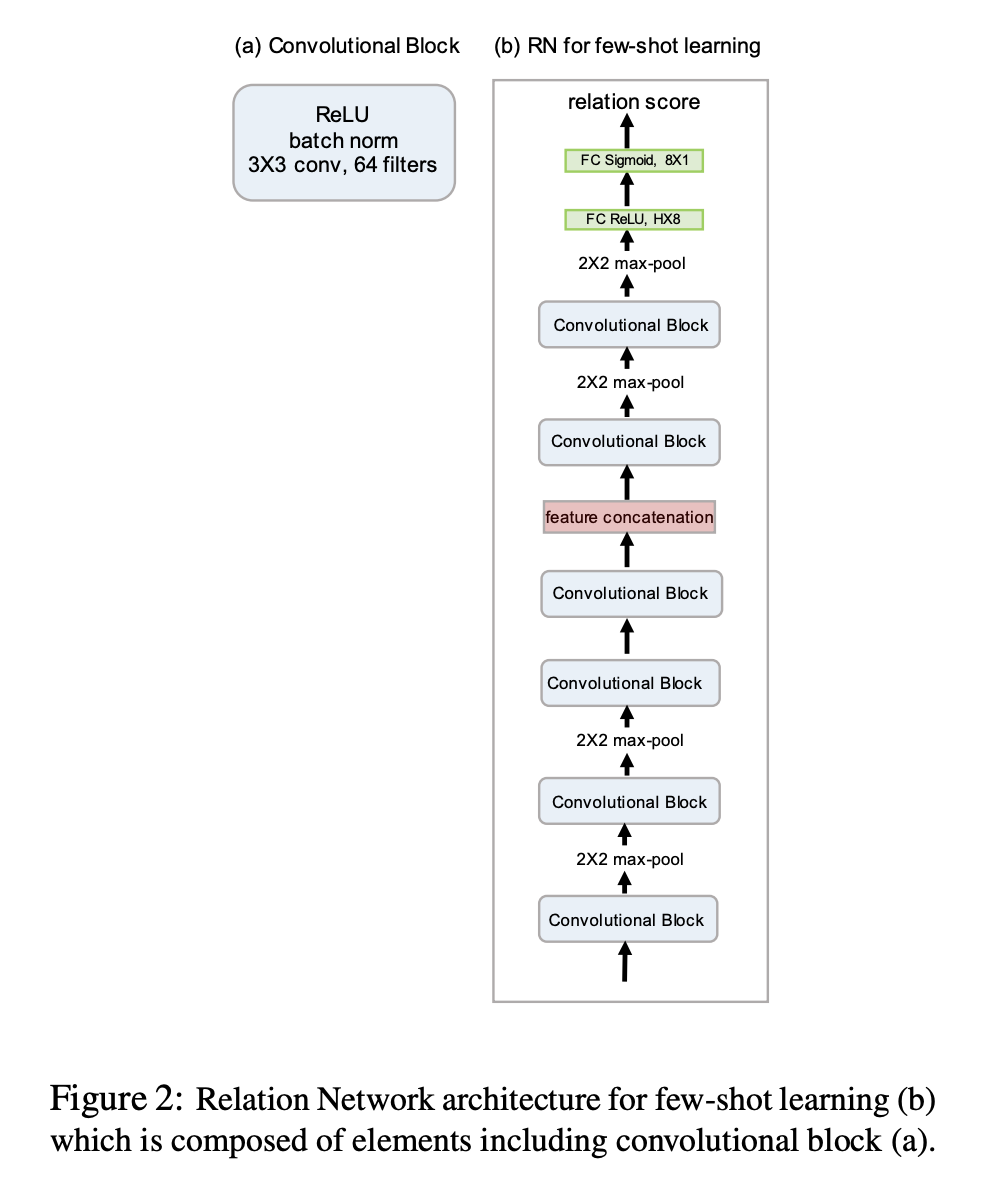
각각의 convolutional block은 64개, 3 x 3 filter를 사용하였고, 이후 batch normalization과 relu를 거쳤다. 첫 두개 block은 2 x 2 max-pooling later를 사용하였는데 이는 output을 relation module의 convolution layer에 입력하기 위해서이다. relation module은 2개의 convolutional block과 2개의 fully connected layer를 사용하였다.

Zero shot learning Network

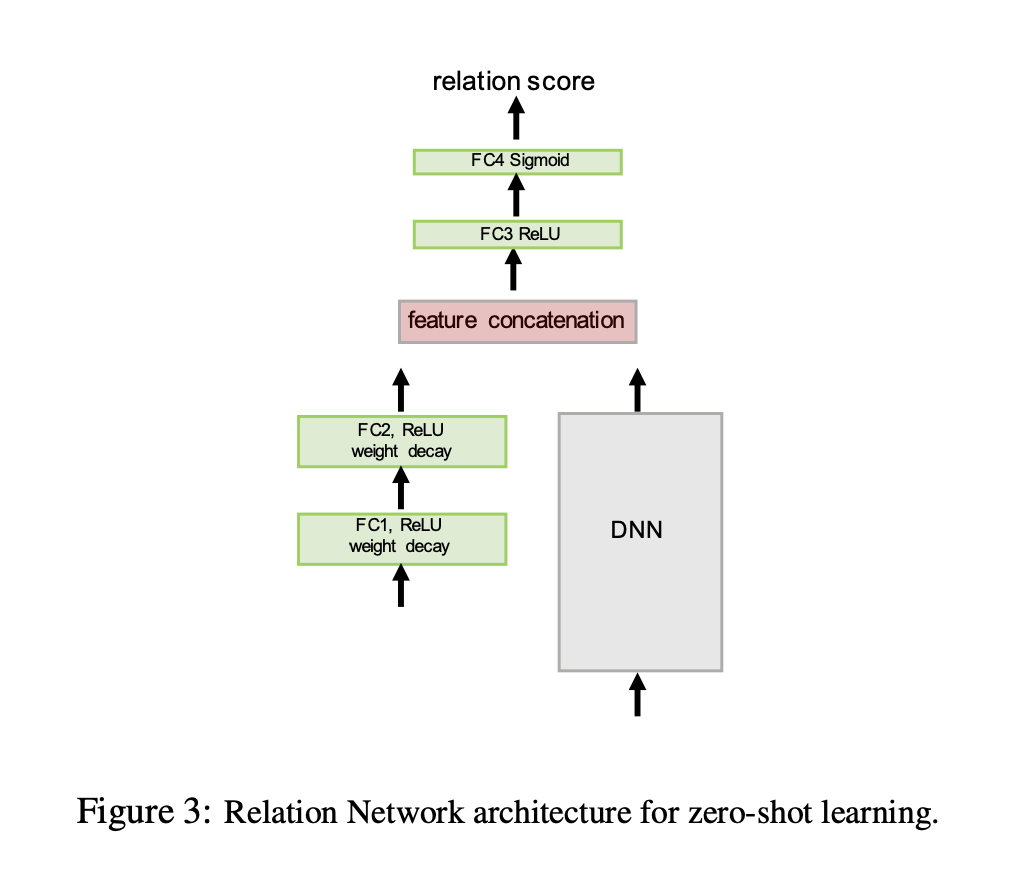
위 그림에서, DNN subnet은 ImageNet의 pretrained 된 network이다.

4. Experiments

Ominglot과 miniImageNet 각각에 relation net을 적용하였고, 결과는 아래와 같다.

4-1. Few-shot Recognition

Adam optimizer를 사용하였고, 100,000 episodes를 사용했다.

1) Ominglot: Dataset, training, result

Dataset

50개 종류의 알파벳을 묘사한 1623개의 Characters를 지니고 있고, 각 class 마다 총 20개의 sample을 지니고 있는 데이터이다. 이를 회전 등과 같은 증강 기법을 통해 데이터를 변형시키고, 1200개는 training, 463개는 testing에 할당하였다.

Training
For each of the C sampled classes in each training episode,
1) 5-way 1-shot: 19 query images
→ 19(query image) x 5(5개의 random class) + 1(1개의 sample image) x 5 = 100 per one episode
2) 5-way 5-shot: 15 query images
3) 20-way 1-shot: 10 query images
4) 20-way 5-shot: 5 query images

Result

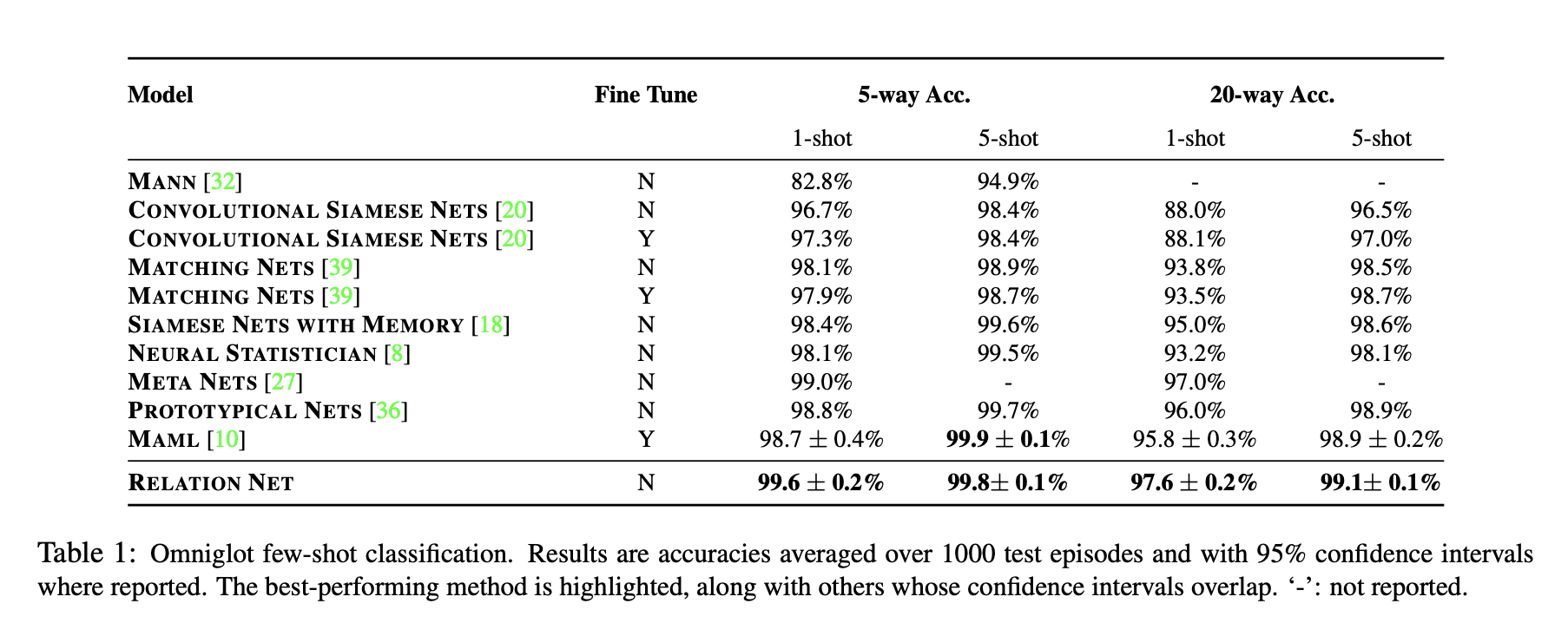
Testing set에서 1000개의 random episode를 만들고, 각 episode의 정확도를 평균으로 하여 성능을 산출하였다. 5-shot 실험에서는, 각 클래스별로 5개의 query image를 뽑았고 (즉, 새로운 하나의 클래스를 판단하는데 고작 5개의 이미지만을 활용한다는 뜻이다. 근데 이 이미지들로 모델의 weight가 바뀌는 것은 아닌 듯하다. fine tuning과는 다른 개념?) 그 결과 5-way 5-shot를 제외하고는 모두 더 높은 정확도를 보였다고 한다.

2) miniImageNet: Dataset, training, result

Dataset
100개의 클래스에 대해 60,000개의 이미지를 지니고 있고, 64, 16, 20개의 class를 각각 train, validation, testing에 할당했다.

Training
5-way 1-shot: 15 query images
→ 15(query image) x 5(5개의 random class) + 1(1개의 sample image) x 5 = 80 per one episode
5-way 5-shot: 10 query images

Result

test set으로부터 600개의 episode를 형성하였고, 각 클래스별로 15개의 query 이미지를 형성하였다. 5-way 1-shot에서 굉장히 좋은 성능을 내었지만, 5-way 5-shot에서는 다른 모델인 prototypical network의 성능이 더 좋다고 나왔다. 다만 확인해본 결과, 해당 모델은 30-way 15 queries로 학습되어야지만 이런 결과를 낼 수 있다고 한다. 동일한 환경인 5-way 5-shot으로 학습시키면 relation net의 결과가 더 좋다고 한다.

4-2) Zero-shot Recogntion

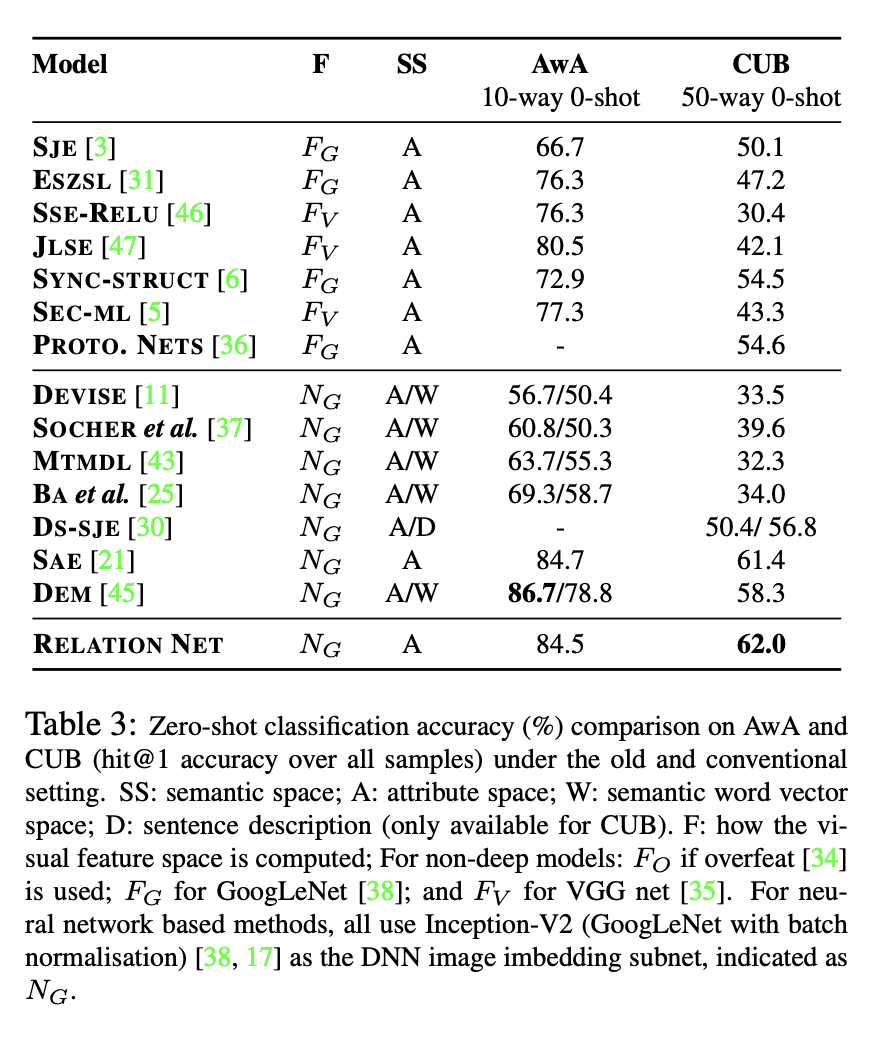
imageNet 1K 데이터를 사용했고, 해당 이미지들의 임베딩 데이터를 vector sample data로 사용하여 학습한 결과가 위와 같다.

5. why does relation Network work?

5-1. relationship to existing models

(Distance metric learning) 기존의 few-shot 논문에서는 주로 fixed metric인 유클리디안 혹은 코사인 distance를 사용했다. 다만 이러한 경우, 모든 학습은 feature map 생성 단계에서만 발생하고, 이미지들간의 관계를 따로 학습하지는 않는다. 이미 관계를 나타내는 metric이 고정되어있기 때문이다. (Conventional metric learning approaches) 해당 접근법은 마할라노비스 metric을 사용하지만, feature representation이 고정되어져 있다. 해당 논문은, 고정된 metric을 relation module로 대체하여 사용했다는 점, 그리고 feature representation을 생성하는 부분도 학습하도록 구성했다는 점에서 해당 논문의 의의를 찾아볼 수 있겠다. 이를 통해, 인간이 정의한 metric이 아닌 실제 데이터의 유사도를 나타내는 true metric을 배울 수 있다. fixed metric은 eleent-wise하고 embedding 이후 linear separability를 가정한다.

[참고] Fixed metrics like assume that features are solely compared element-wise, and the most related assumes linear separability after the embedding. These are thus critically dependent on the efficacy of the learned embedding network, and hence limited by the extent to which the embedding networks generate inadequately discriminative representations. In contrast, by deep learning a nonlinear similarity metric jointly with the embedding, Relation Network can better identify matching/mismatching pairs.

5-2. Visualisation

[논문에서] To illustrate the previous point about adequacy of learned input embeddings, we show a synthetic example where existing approaches definitely fail and our Relation Network can succeed due to using a deep relation module. Assuming 2D query and sample input embeddings to a relation module, Fig. 4(a) shows the space of 2D sample inputs for a
fixed 2D query input. Each sample input (pixel) is colored
according to whether it matches the fixed query or not. This represents a case where the output of the embedding modules is not discriminative enough for trivial (Euclidean NN) comparison between query and sample set. In Fig. 4(c) we attempt to learn matching via a Mahalanobis metric learning relation module, and we can see the result is inadequate. In Fig. 4(d) we learn a further 2-hidden layer MLP embedding of query and sample inputs as well as the subsequent Mahalanobis metric, which is also not adequate. Only by learning the full deep relation module for similarity can we solve this problem in Fig. 4(b).

실제로 임베딩을 잘 학습했는지 확인하기 위해 저자는 embedding을 직접 시각화를 진행하였다. 2d query와 sample이 존재한다고 가정하고, 이를 학습시켜보았다고 가정하자. 위의 (a)는 2d sample input의 space를 실제로 묘사한 결과이다. 각각의 샘플은 fixed query와 매치되었는지 아닌지로 coloring이 되어져 있다. 그림에서 보이듯이 relation net이 가장 잘 묘사한 것을 발견할 수 있다.

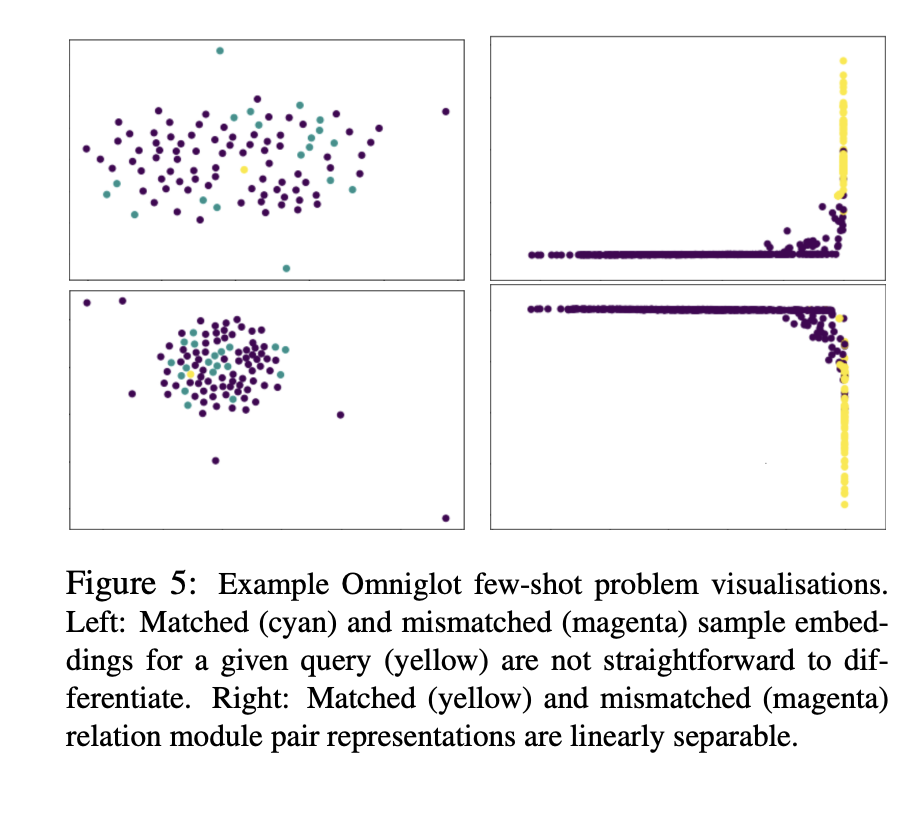
실제 문제에서, embedding을 비교하는 문제는 그렇게 어렵진 않지만, 여전히 도전적인 과제이다. 저자는 2개의 ominglot query image embedding을 matching하였고 위 그림이 그 결과다. 시각화한 결과, fixed metric을 사용한 경우 match하는 쿼리와 mismatch하는 쿼리가 모두 한 곳에 모여져 있다. relataion net내에서의 embedding은 그림의 오른쪽 표와 같이 match와 mismatch가 명확하게 구분되어져 있는 것을 볼 수 있다.

[논문에서] In a real problem the difficulty of comparing embeddings may not be this extreme, but it can still be challenging. We qualitatively illustrate the challenge of matching two example Omniglot query images (embeddings projected to 2D, Figure 5(left)) by showing an analogous plot of real sample images colored by match (cyan) or mismatch (magenta) to two example queries (yellow). Under standard assumptions the cyan matching samples should be nearest neighbours to the yellow query image with some metric (Euclidean, Cosine, Mahalanobis). But we can see that the match relation is more complex than this. In Figure 5(right), we instead plot the same two example queries in terms of a 2D PCA representation of each query-sample pair, as represented by the relation module’s penultimate layer. We can see that the relation network has mapped the data into a space where the (mis)matched pairs are linearly separable.

6. Conclusion

relation network는 임베딩과 쿼리셋과 sample set간의 비선형적인 distance metric을 학습한다. 이러한 접근법은 기존의 방법들보다 간단하고 효율적이고, sota 성능을 이끌어냈다는 점에서 의미를 찾을 수 있다.

7. Relation Net Code

FSL github