https://www.acmicpc.net/problem/1149

---

문제 설명

RGB거리에는 집이 N개 있다. 거리는 선분으로 나타낼 수 있고, 1번 집부터 N번 집이 순서대로 있다.

집은 빨강, 초록, 파랑 중 하나의 색으로 칠해야 한다. 각각의 집을 빨강, 초록, 파랑으로 칠하는 비용이 주어졌을 때, 아래 규칙을 만족하면서 모든 집을 칠하는 비용의 최솟값을 구해보자.

1번 집의 색은 2번 집의 색과 같지 않아야 한다.
N번 집의 색은 N-1번 집의 색과 같지 않아야 한다.
i(2 ≤ i ≤ N-1)번 집의 색은 i-1번, i+1번 집의 색과 같지 않아야 한다.

입력
첫째 줄에 집의 수 N(2 ≤ N ≤ 1,000)이 주어진다. 둘째 줄부터 N개의 줄에는 각 집을 빨강, 초록, 파랑으로 칠하는 비용이 1번 집부터 한 줄에 하나씩 주어진다. 집을 칠하는 비용은 1,000보다 작거나 같은 자연수이다.

출력
첫째 줄에 모든 집을 칠하는 비용의 최솟값을 출력한다.

---

풀이

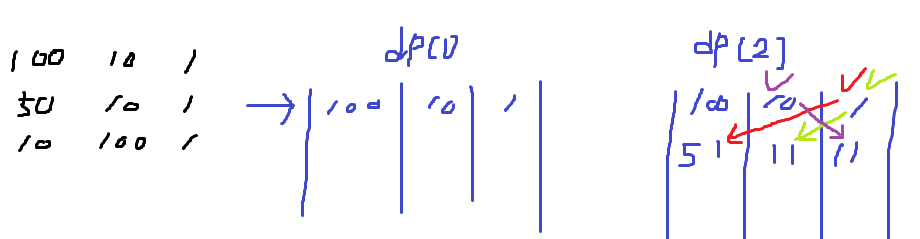
두번째 집을,

• 빨갛게 칠할 때 싸게 칠하고 싶다면 첫번째 집에서 파랗게 칠해야 함 (비용이 1)
• 초록색으로 칠할 때 싸게 칠하고 싶다면 첫번째 집에서 파랗게 칠해야 함
• 파랗게 칠할 때 싸게 칠하고 싶다면 첫번째 집에서 초록색으로 칠해야 함(1짜리는 같은 파랑이라 안돼서, 그나마 싼 10으로)

각 집을 무슨 색으로 칠하냐에 따라 상황이 달라지고 비용이 달라지므로 dp배열은 그림처럼 이차원 배열로 두어야 함

import java.util.Arrays;
import java.util.Scanner;

public class B1149_RGB거리 {
	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		int N = sc.nextInt();
		int[][] map = new int[N][3];
		int[][] dp = new int[N + 1][3];

		for (int i = 0; i < N; i++) {
			for (int j = 0; j < 3; j++) {
				map[i][j] = sc.nextInt();
			}
		}

		for (int i = 1; i <= N; i++) {
			dp[i][0] = map[i-1][0] + Math.min(dp[i - 1][1], dp[i - 1][2]);
			dp[i][1] = map[i-1][1] + Math.min(dp[i - 1][0], dp[i - 1][2]);
			dp[i][2] = map[i-1][2] + Math.min(dp[i - 1][0], dp[i - 1][1]);
		}
		System.out.println(Math.min(dp[N][0], Math.min(dp[N][1], dp[N][2])));
	}
}

결과

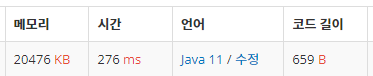
좀 느리고 메모리 큰 편임