1. 정의

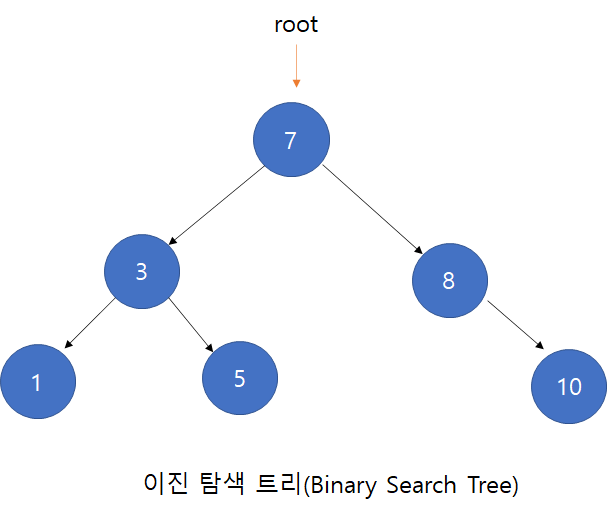
아래의 특징을 가지는 이진트리(각 노드의 자식 노드가 최대 2개인 트리)를 말한다.

1. 각 노드에 중복되지 않는 키(key)가 있다.

2. 루트노드의 왼쪽 서브 트리는 해당 노드의 키보다 작은 키를 갖는 노드들로 이루어져 있다.

3. 루트노드의 오른쪽 서브 트리는 해당 노드의 키보다 큰 키를 갖는 노드들로 이루어져 있다.

4. 좌우 서브 트리도 모두 이진 탐색 트리여야 한다. 

아래와 같은 트리가 이진탐색트리이다.

2. 특징

-기존 이진트리보다 탐색이 빠르다.

-최대 O(h)의 시간 복잡도를 가진다.(height)

3. Search, Insert, Delete

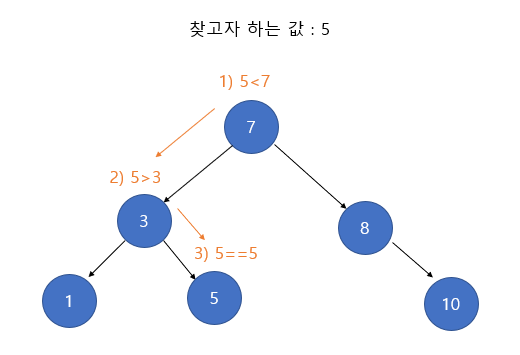
[Search] <search(key)>

1. 루트 노드의 키와 찾고자 하는 값을 비교한다. 찾고자 하는 값이라면 탐색을 종료한다.

2. 찾고자 하는 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리로 탐색을 진행한다.

3. 찾고자 하는 값이 루트노드의 키보다 크다면 오른쪽 서브트리로 탐색을 진행한다. 

탐색 과정이 위와 같아서 최대 O(h)의 시간 복잡도를 가지는 것이다.

예시는 아래와 같다.

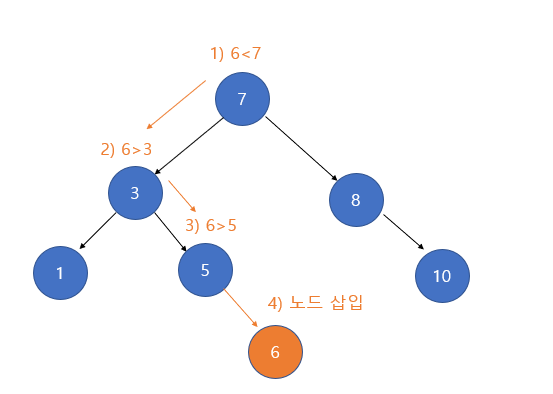
[Insert] <insert(n)>

1. 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다.

(중복 값 허용 X)

2. 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

3. 삽입할 값이 루트노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

예시는 아래와 같다.

[Delete] <remove(n)>

Delete의 경우 아래와 같이 3가지 상황을 나눠서 구현해야한다.

1. 삽입할 값을 루트 노드와 비교해 같다면 오류를 발생한다.

(중복 값 허용 X)

2. 삽입할 값이 루트 노드의 키보다 작다면 왼쪽 서브 트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

3. 삽입할 값이 루트노드의 키보다 크다면 오른쪽 서브트리를 탐색해서 비어있다면 추가하고, 비어있지 않다면 다시 값을 비교한다.

[참고문헌]-감사합니다.
https://code-lab1.tistory.com/10