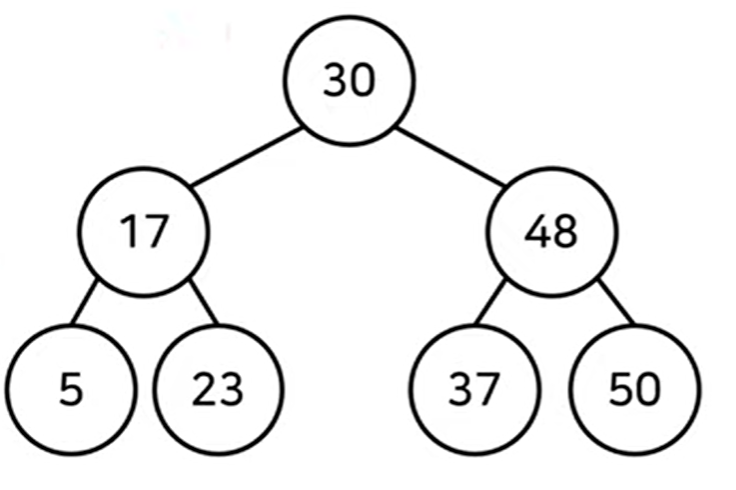
✨ 트리

한 개 이상의 노드로 이루어진 사이클이 없는 연결그래프
계층적인 구조를 표현할 때 사용할 수 있는 자료구조
(트리의 노드개수가 N개일 때, 전체 간선의 수는 N-1개)

• 루트노드 : 부모가 없는 최상위 노드

• 단말노드 : 자식이 없는 노드

• 크기 : 트리에 포함된 모든 노드의 개수

• 깊이 : 루트노드부터의 거리

• 높이 : 깊이 중 최댓값

• 차수 : 각 노드의 간선 개수

✅ 이진 탐색 트리

이진 탐색이 동작할 수 있도록 고안된 효율적인 탐색이 가능한 자료구조

• 왼쪽 자식노드 < 부모 노드 < 오른쪽 자식노드

• 검색과 저장, 삭제의 시간복잡도는 모두 O(logn), worst case는 한쪽으로 치우친 트리가 됐을 때 O(n)

• 저장과 동시에 정렬을 하는 자료구조

• BST의 worst case 시간 복잡도는 O(n)이고 균형이 깨져서 한쪽으로 치우친 BST의 경우 linked list와 같아지며 탐색시에 O(n)이 된다.

✅ 트리의 순회

트리의 자료구조에 포함된 노드를 특정한 방법으로 한번씩 방문하는 방법
트리의 정보를 시각적으로 확인

• 전위순회 : 루트를 먼저 방문

• 중위순회 : 왼쪽자식을 방문하고 루트를 방문

• 후위순회 : 왼쪽자식, 오른쪽 자식, 루트 방문

❓ 이진트리로 Directory를 관리하고 있다고 가정할 때 Directory 용량을 알고싶다면 어떠한 탐색을 해야하는가?

=> 후위 순회

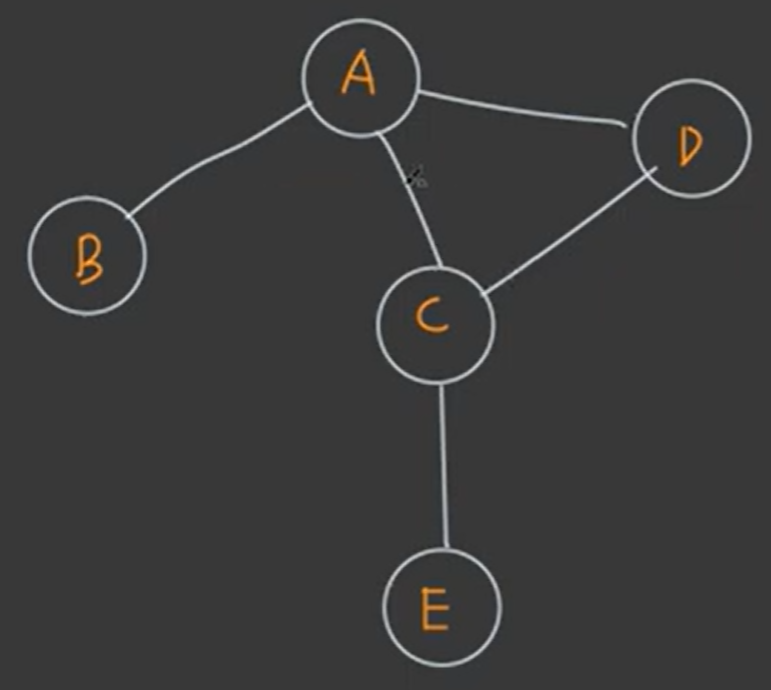
✨ 그래프

vertex와 dege로 구성

• Direction의 유무
  • 방향성이 없다면 undirected Graph
  • 방향성이 있다면 directed Graph
• Cycle의 유무
  • 순환이 있다면 Cyclic Graph
  • 순환이 없다면 Acyclic Graph
• Weight의 유무
  • 가중치가 있다면 weighted Graph

✅ 그래프를 표현하는 2가지 방법

• 인접행렬 (Adjacency Matrix)

1. 연결여부를 상수시간안에 확인 가능
2. 가중치 표현 편리
3. 메모리 공간 낭비
4. 메모리 요구량 증가

• 인접리스트 (Adjacency List)

1. 공간 효율성
2. 추가 및 갱신 연산 효율성
3. 연결 정보 확인시간 증가
4. 고립된 노드 처리 어려움

✅ 그래프를 검색하는 2가지 방법

1. DFS (깊이 우선 탐색)

• 전위, 후위, 중앙 순회 탐색을 이용
• Stack으로 구현 가능

2. BFS (너비 우선 탐색)

• Level 단위 탐색을 이용
• Queue로 구현 가능