AE, VAE, GAN

DONGJIN IM·2022년 3월 7일

AI 이론

AI(NLP) 이론

목록 보기

10/18

https://deepinsight.tistory.com/126
AE와 VAE에 대해 자세히 공부한 사이트
매우 정리가 잘 되어 있으므로 참조
https://m.blog.naver.com/euleekwon/221557899873
- GAN에 대한 정리가 깔끔히 되어 있는 사이트

AutoEncodeer

입력과 출력이 같은 구조로써, 중간에 Bottleneck Hidden Layer를 활용하여 Encode와 Decode를 수행한다.

높은 차원을 낮은 차원으로 변경시키는 과정에서 원본 Data 중 의미 있는 속성들(Meaningful Properties)를 추출하는 Dimensionality Reduction을 수행한다.

고차원 데이터를 Error 없이 잘 표현하는 Subspace를 Manifold라고 하는데, AE는 Manifold Learning을 통해 학습이 진행된다.
Manifold Learning의 목적은 차원을 잘 축소하여 데이터의 특징을 잘 추출하는 것이다.

출처 : https://deepinsight.tistory.com/126
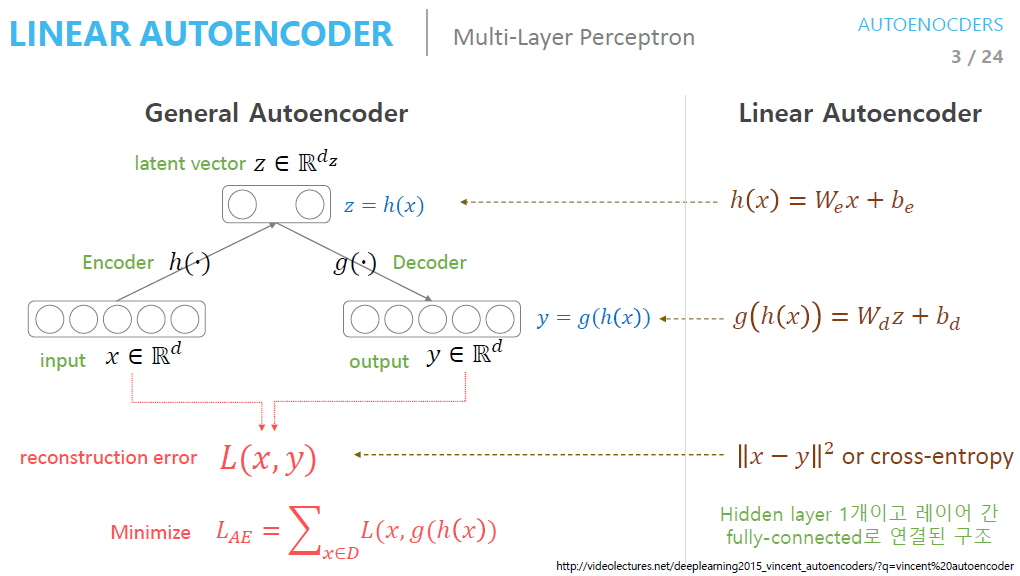
사진에 대한 설명
- Input Data를 Encoder Network에 통과시켜 압축된 Z 값을 얻음
  - Z : Latent Vector
  - Latenet Variable : Latent Vector들을 모아 놓은 Hidden Layer
  - Latent variable = Bottleneck Layer = Feature = Hidden Representation
- Latent Vector z를 Deocder에 통과시켜 Input Data와 같은 크기의 출력 값 생성
- Loss : Input Data x와 Decoder를 통과한 y의 차이

VAE

VAE란?

Auto Encoder 개념을 활용하여 Generative Model로써, Explicit Density이긴 하지만, Approximate Density Model이다.
Input Data에 대한 Model을 구할 수는 없지만, Input Data Model에 근사하는 (Approximate) Model을 형성하는 것이다.
Input Data에 대한 Model이 존재는 하니 Explicit Density Model이긴 하지만, 실제 Data에 적합한 Model이라기 보다는 내가 예측한 모델이라고 보는 것이 정확하다.

AE는 잠재 공간(Latent Variable)에 값을 저장하지만, VAE는 잠재 공간에 확률 분포를 저장하므로, 평균과 분산 파라미터를 생성한다.
또한, AE는 Manifold Learning이지만, VAE는 Generative Model이라는 차이점이 존재한다.

AE의 목적은 input x에 대해 자신을 언제든지 reconstruct 할 수 있는 "z를 만드는 것"이다.
즉, 주 목적은 Encoder를 학습시켜 Latent space인 z를 만드는 것이 목표이며, 학습을 위해 Decoder를 뒷단에 붙여 최종 형태가 생성되는 것이다.

VAE의 목적은 input x가 만들어지는 확률 분포를 찾고, 다른 Data에 대해 이 확률 분포(Variational Distribution)를 활용하는 것이다.
우리가 원하는 것은 z(Latent space; 즉, 사진의 특징들)를 Decoder에 통과시켜 결과물을 얻는 것이다.
즉, Decoder를 학습시키는 것이 목표이다.
Decoder를 학습시키기 위해 Encoder를 앞단에 붙여 특징을 뽑는 과정이 추가된 것이다.

이러다보니, 전혀 다른 목적을 위해 만들어졌지만 어쩌다 보니 형태가 비슷해져 비슷한 이름을 가지게 되는 것이다

VAE가 Approximate Model을 찾는 이유

우리의 궁극적인 목표는 Posterior distribution을 찾는 것이다.
(Posterior Distribution : 관심을 가진 Random Variable의 확률 분포)

이 때, Posterior distribution은 베이즈 정리에서 사후 확률을 의미한다.
베이즈 정리를 확인하면 이 값을 계산하기 위해선 Likelihood(모델에서 데이터 값이 나올 확률)와 사전확률이 필요하다는 것을 알 수 있다

그런데, VAE는 intractable model이다. 간단히 말하자면, 입력 Data들을 모두
만족 시키는 실제 Model을 찾기 매우 어렵다는 의미이다.
실제 Model을 찾기 어렵기 때문에, Likelihood를 찾기도 매우 어려워 질 것이다
(모델을 구할 수 없으므로, 모델에서 데이터 나올 확률도 구하기가 당연히 어려움)

따라서, Posterior Distribution과 "근사하는" Approximate Distribution을 만드는 것이고, 이를 위해 학습을 통해 얻을 수 있는 Variational Distribution을 찾는 것이다

그림으로 이해하는 VAE

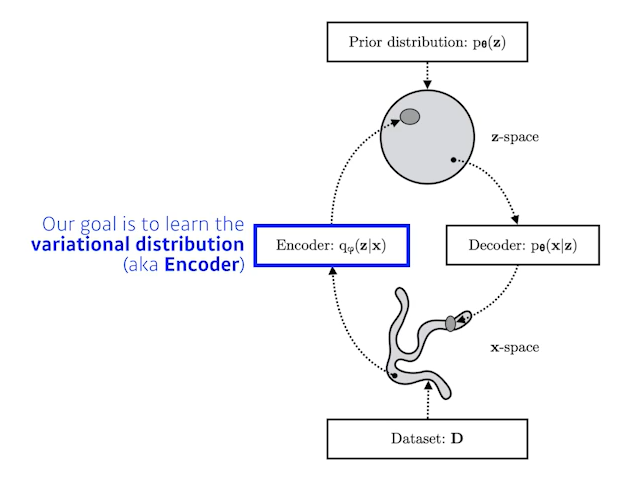
Data를 Encoder를 통해 Bottleneck Layer(z-space)를 생성한다.

궁극적 목표는 Data를 Latent Space로 보내는 Encoder 함수를 통해 생성되는 Variational distribution을 최적화시키는 것으로써, Variational Distribution이 최적화되면, Decoder로 만든 Data가 실제 Data와 매우 유사해질 것이다.

VI란?

VAE를 공부하면 이해가 안 될 수 있다. 우리는 Posterior Distribution을 모른다.
그런데, Posterior Distribution과 근사한 것을 찾아야 하는 것이다.

우리는 외계인이 어떻게 생긴지 모른다. 그런데 외계인과 가까운 생명체를 만들어 내라고 한다. 그렇다면, 내가 어떤 생명체를 생성해냈을 때, 이 생성체가
얼마나 외계인과 가까운지 비교를 할 수가 있을까?

위 예시를 Model을 통해 설명하자면, Posterior Distribution을 구할 수가 없는데, Approximate Distribution을 찾았다고 하면 Loss는 어떤 식으로 측정할까?

이를 위해 활용하는 방식이 VI이다.

수식으로 이해하는 VI

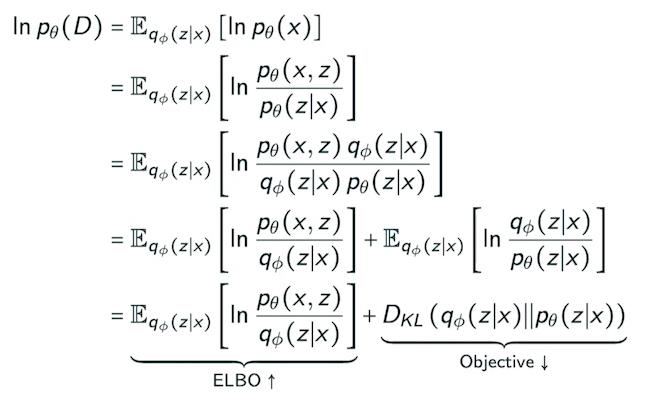
수식 용어 정리
- p(x|z) : True Posterior Distribution
  - Intractable 하므로 구할 수 없음
- p(z) : 아무런 조건이 없을 때 Latent Variable의 분산 정도
- q(z|x) : Approximation Function

우리는 최종적으로 p(x)를 최적화하기를 원한다. 위 수식을 그대로 따라가보면, p(x)는 결국 ELBO와 $D_{KL}$ 을 통해 구할 수 있음을 알 수 있다.( $D_{KL}$ : KL Divergence)

그런데, 우리는 p(z | x)를 구할 수 없다고 했다. 즉, $D_{KL}$ 은 두 확률 분포 사이의 거리이기 때문에, p(z | x)를 구할 수 없는 이상 $D_{KL}$ 도 구할 수 없을 것이다

하지만, 수식에서 ELBO 값이 커지면 $D_{KL}$ 이 작아짐을 알 수 있다. 우리는, Approximate(q(z | x))와 True Posterior(p(z | x))의 거리가 가까워야 함을 알 수 있고, 이는 $D_{KL}$ 이 작아야 한다는 말과 동일한 의미이다.

즉, ELBO를 크게 만들어야 한다.

그렇다면, ELBO 식을 한 번 정리해보자

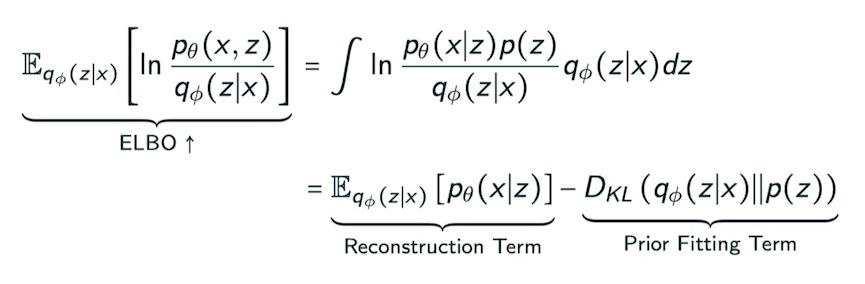
Reconstruction Term : AE에서의 Reconstruction Loss
- Input Data x와 Decoder를 거쳐 반환된 y Data와의 차이
Prior Fitting Term : 우리가 만든 Approximation Function과 p(z)와의 거리
- p(z) : Prior Distribution. 사전 확률. 관측자가 관측을 하기 전 기본적으로 가지고 있는 확률 분포

이전에 설명해야 할 것이 있다. p(z)가 정확히 무엇을 의미하는가?

위에서는 아무 조건이 없을 때 Latent Variable의 확률 분포라고 포함하였다. 그리고, 위에서는 사전 확률이라고 말하였다. 무엇이 맞는 것일까?

정답은, 둘 다 맞는 말이다. 결국, 내가 학습하기 이전에 Latent Variable의 확률 분포를 볼 수 있을 것이다. 그리고, "학습이 진행되기 이전"의 확률 분포이기 때문에, 관측하기 전에 가지고 있는 확률 분포라고 생각할 수도 있다.

그렇다면, 어떻게 p(z)를 알 수 있을까? 베이지안에서도 사전 확률을 설정하기가 매우 어려움을 알 수 있었는데 말이다.

우리는 p(z)를 N(0,1), 즉 normal distribution으로 둔 이후에 Sampling을 진행한다.

이유는, 우리가 사용하는 Network는 Deep Neural Network이기 때문이다.

Bayes' Rule에서 말했듯, 계속해서 사전 확률은 Update 된다. 그리고, 사전 확률이 update 될 수록 정확도는 늘어난다.

Deep Neural Network는 여러 epoch만큼 학습이 진행되고, 앞 단에 있는 몇 개의 Layer들은 Manifold를 잘 찾기 위한 역할을 수행한다. 즉, p(z)를 최적화 시켜 Latent Vector에 맞는 Distribution을 생성하는 것이다. 따라서, p(z)(사전 확률)을 무엇으로 지정해야 하는지 고민하지 않아도 된다

그럼, 우리는 위 수식을 통해 결국 VAE에게 바라는 점은 ELBO를 키우는 것이고, 그 방법은 2가지 존재한다는 것을 알 수 있다

Condition : Approximation function의 값이 최대한 prior 값과 동일하게 만들어야 함 ⇒ Prior fitting Term을 작게 하는 방법(KL Divergence이므로 거리를 최대한 줄임)
Generation : Approximation function으로 생성한 z를 다시 Decoder를 통해 복구시킨 y값에 대하여, y와 input data가 유사해야함 ⇒ Reconstruction Term

따라서, 위 ELBO 수식으로 우리는 Loss function을 구할 수 있을 것이며, 우리가 학습시켜야 할 Approximation function은 q(z|x)이므로 이를 학습시키면 될 것이다.

(즉, Data들을 처리했을 때, Latent Distribution과 가장 유사하게 만드는 Approximation function을 만드는 것이 최종적인 목표라고 할 수 있다)

VAE에서 Gaussian Normal Distribution(N(0,1))을 활용하는 이유

한 마디로 말하자면, 적분 값을 Closed Form으로 뽑아낼 수 있는 몇 안되는 식이기 때문이다.

학습을 진행하면서 미분이 필수적으로 필요한데, KL Divergence 같은 경우 계산식 자체에 적분이 들어가 있다.
그런데, 이 적분 값을 Closed form으로 뽑아낼 수 있어야지만 학습을 통해 개선이 가능하다
VAE에서 Closed Form을 뽑아낼 수 있는 몇 안되는 식이 Gaussian이므로, VAE에서는 주로 "isotropic Gaussian"을 활용하게 되는 것이다.

AAE(Adversarial AutoEncoder) : Gaussian만 활용할 수 있는 VAE의 단점을 보완하기 위하여 Gaussian 대신 GAN을 활용하여 분포를 맞춰주는 것

Closed Form이란?

값을 대입하였을 때, 계산을 통해 정확한 값이 도출되는 수식을 Closed Form이라고 한다.
$\int _{\ }^{\ }e^{-x^2}dx$ 같은 경우 직접적인 적분이 불가능하다. 따라서 Closed Form이 아니다.
하지만, $\int _{\ }^{\ }xe^{-x^2}dx$ 같은 경우 $x^2$ 을 t로 치환하여 적분을 깔끔하게 특정 식으로 처리할 수 있다. 따라서, Closed Form이다.

Prior Fitting Term

우리는 KL Divergence에서 p(z)를 Normal Distribution으로 설정할 수 있음을 알 수 있었다.
KL Divergence의 p(z)에 N(0,1)을 넣으면 아래와 같이 깔끔하게 수식으로 정리되므로, 해당 수식을 Loss Function에 입력하면 된다.

D_{KL}\left(q\ \left(z\ \mid \ x\right)\ \mid \ N\left(0,1\right)\right)\ =\ \frac{1}{2}\sum _{i=1}^D\left(\sigma _{z_i}^2+\ \mu _{z_i}^2\ -\ \ln \left(\sigma _{z_i}^2\right)\ -\ 1\right)

GAN

GAN 동작 방식

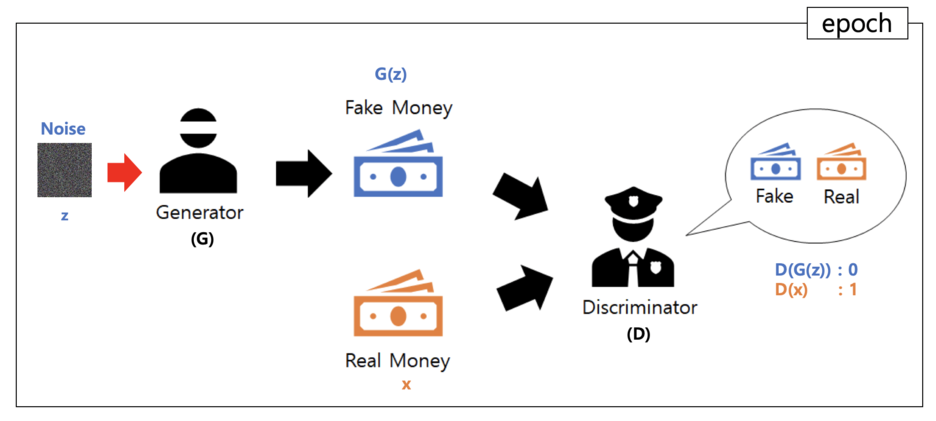
사진 출처 : https://m.blog.naver.com/euleekwon/221557899873

Fake Data(Generative Model을 통해 만들고자 하는 Data)를 만들고, 이것을 Discriminator가 Fake인지 True인지 판별하여 Discriminator가 Fake와 실제 Data를 구분하지 못할 때까지 Fake Data를 만드는 Generator를 학습시키는 것이 모델의 큰 틀이라고 말할 수 있을 것이다.

가장 대중적인 설명은 지폐 위조범(Generator;G)와 경찰(Discriminator;D)에 빗대어 설명한 것이다

Generator는 Nois(0~1 사이 쓰레기 Data)를 활용하여 위조 지폐(G(z))를 만든다.
- Latent Code로부터 얻은 Noise를 통해 Generative Model은 Fake Data를 생성
Discriminator는 위조 지폐(G(z))와 실제 지폐(x)를 구분하는 작업을 수행한다.
실제 지폐라면 D(x) = 1, 위조 지폐라면 D(G(z)) = 0을 반환한다.
- Discriminator는 Fake Data와 실제 Data를 랜덤하게 받아 Data가 Model이 만든 Data인지 실제 Data인지 0 혹은 1을 반환함으로써 알려줌
경찰이 위조 지폐와 진짜 지폐를 잘 구분하면, Generator는 해당 결과를 활용하여 더욱 정밀하게 위조 지폐를 만든다. 동시에 경찰은 교육을 조금 더 상세히 받아 위조 지폐범(G)가 만든 위조 지폐와 실제 지폐를 조금 더 정밀하게 비교한다.
- D, G 모두 교육을 수행하여 G는 D를 속일만큼의 Data를 생성하고, D는 G에게 속지 않도록 교육 받음
최종적으로 경찰이 위조 지폐와 진짜 지폐를 잘 파악하지 못하면 학습이 끝난다.
- 위조 지폐를 잘 구분하지 못하면 결국 찍는 수 밖에 없으므로, 50%로 정확도가 수렴한다.

Discriminator & Generator

Discriminator
Supervised Learning으로 학습이 진행된다.
Data가 Input으로 들어 왔을 때 진짜(1)인지 가짜(0)인지를 Output으로 반환하며 Classifying하며 학습을 진행한다.
Generator 모델
Unsupervised Learning으로 학습이 진행된다.
Latent Code(잠재 코드)를 가지고 이 데이터가 Training 데이터로 변환되도록 변화시키며 학습한다.
계속해서 학습을 진행하므로 Generator가 학습 가능하다는 것이 장점이다.

GNA 특징

Generator가 받는 Random Noise Input z를 조금씩 변형시켜 Generator를 이미지의 미세한 조정으로 분포할 수 있음
- 생성할 Data를 미세하게 변경 할 수 있음
VAE에 비해 학습이 매우 어려움
- D를 Maximize하는 동시에 G를 Minimize 해야하므로, Gradient Update가 어려움
VAE보다 깔끔한 이미지를 만들 수 있음

VAE와 GAN의 차이

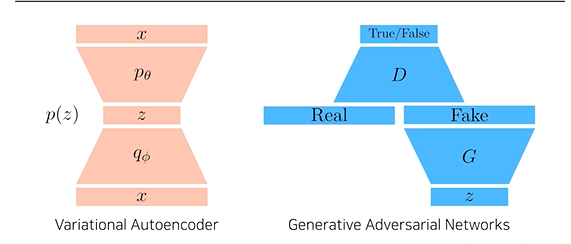
VAE : Latent Code를 거쳐 Feature를 뽑았다 다시 데이터 생성
GAN : Fake Data를 활용하여 다시 학습 진행

수식을 통한 GAN 이해

전체 수식

$\min_G\ \max_D\ V\left(D,\ G\right)\ =\ E_{x\ \sim \ P_{data}\left(x\right)}\left[\log D\left(x\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ E_{z\ \sim \ P_z\left(z\right)}\left[\log \left(1\ -\ D\left(G\left(z\right)\right)\right)\right]$

$E_{x\sim P_{data}(x)}[log D(x)]$ : x가 $P_{data}(x)$ (실제 Data)의 Distribution 중 1개 값이라는 의미
min max V(D,G) : D에 대해서는 Max 값을 만들어야 하며, G에 대해서는 Min 값을 만들어야 함
G(z) : z라는 Noise를 통해 만든 Fake Data
- z를 Gaussian Distribution에서 랜덤하게 뽑음

Discriminator 입장에서의 수식

$\max _D^{ }\ V\left(D,\ G\right)\ =\ E_{x\ \sim \ P_{data}\left(x\right)}\left[\log D\left(x\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ E_{z\ \sim \ P_z\left(z\right)}\left[\log \left(1\ -\ D\left(G\left(z\right)\right)\right)\right]$

V(D,G) 값의 최대치를 원하므로 D(x) = 1, D(G(z)) = 0이 되도록 만드는 것이 목표
- 실제 Data는 1을, Fake Data는 0을 반환
- 최대치를 구하는데 log(x)를 0으로 만드는 1을 활용한다는 게 이상하다고 생각할 수 있지만, D(x)는 0과 1 사이의 값을 가지므로 log 함수는 log(1)일때가 최댓값이 됨을 알 수 있다.
V(D,G)를 최대로 만드는 Optimal Discriminator
$D_G^*\left(x\right)\ =\ \frac{P_{data}\left(x\right)}{P_{data}\left(x\right)\ +\ P_G\left(x\right)}$
- 수식 유도

Geneartor 입장에서의 수식

$\min _G^{ }\ V\left(D,\ G\right)\ =\ E_{x\ \sim \ P_{data}\left(x\right)}\left[\log D\left(x\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ E_{z\ \sim \ P_z\left(z\right)}\left[\log \left(1\ -\ D\left(G\left(z\right)\right)\right)\right]$

Generator는 Discriminator의 정확도에 대해 관심이 없음
- log(D(x))에 대해 전혀 관심을 주지 않음
- 오로지 D(G(z)) = 1이 되는 것에만 관심을 줌
Generator 수식에 Optimal Discriminator를 Plug in한 수식
- Loss Function을 구하는 과정
  $V\left(G,\ D_G^*\left(x\right)\right)\ =\ E_{x\sim P_{data}}\left[\log \ \left(D_G^*\left(x\right)\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\ E_{z\ \sim \ P_z}\left[\log \left(1-D_G^*\left(G\left(z\right)\right)\right)\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ E_{x\sim P_{data}}\left[\log \ \left(D_G^*\left(x\right)\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad E_{z\ \sim \ P_g}\left[\log \left(1-D_G^*\left(x\right)\right)\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ E_{x\sim P_{data}}\left[\log \ \left(\frac{\rho _{data}\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad E_{z\ \sim \ P_g}\left[\log \left(\frac{\rho _g\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ E_{x\sim P_{data}}\left[\log \ \left(\frac{\rho _{data}\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad E_{z\ \sim \ P_g}\left[\log \left(\frac{\rho _g\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\\ \\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ E_{x\sim P_{data}}\left[\log \ \left(\frac{\rho _{data}\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\ +\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad E_{z\ \sim \ P_g}\left[\log \left(\frac{\rho _g\left(x\right)}{\rho _{data}\left(x\right)\ +\ \rho _g\left(x\right)}\right)\right]\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ KL\left(p_d\ \mid \mid \ p_d\ +\ p_g\right)\ + KL\left(p_g\ \mid \mid \ p_d\ +\ p_g\right)\\ \ \ \ \ \ \ \ \ \ \ \ \ =\ KL\left(p_d\ \mid \mid \frac{\ p_d\ +\ p_g}{2}\right)\ +\ KL\left(p_g\ \mid \mid \ \frac{p_d\ +\ p_g}{2}\right)\ -\ \log \left(4\right)\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ =\ 2JS\left(p_d\ \mid \mid \ p_g\right)\ -\ \log \left(4\right)$

JS-Divergence는 Non-Negative한 Metric이므로, Loss가 가장 낮은 경우는 -log(4)의 값을 가진다.
즉, Loss 값이 가장 낮아질 때는 $P_{data} = P_g$ 인 상황이다. 실제 Data 분포와 Generator가 만든 Data의 분포가 동일하여, Discriminator가 둘을 구별하지 못하고 결국 (찍어서) 50%의 정확도를 가지는 상황이 가장 Loss가 낮아질 때가 되는 것이다.

하지만, 여기에서 JS를 낮춘다는 말이 조금은 이상할 수 있다.
Discriminator 자체가 처음부터 완벽하지 않다. 위조 지폐범과 경찰으로 예시를 들자.
인간, 즉 Data를 볼 우리들은 매우 능력이 뛰어난 경찰이다. 그리고 결국 위조 지폐범은 인간인, 매우 능력이 뛰어난 경찰을 속여야 한다.
그런데, Discriminator는 처음에는 신입 경찰이다. 즉, 위조 지폐 구분 능력이 그렇게 뛰어나지 않다. 하지만, 우리는 Generator가 Discriminator의 판독 결과를 활용하여 학습한다는 것을 알고 있다. 무능한 경찰이 구분한 Data를 활용하여 학습을 수행하고, 이를 통해 뛰어난 경찰(인간)을 속여야 한다는 것이다.

즉, Discriminator 자체가 처음부터 완벽하지 않기 때문에 동시에 학습시키면서 JS를 낮춘다는 말이 어떻게 보면 말이 안되는 것이다.

GAN의 발전

DCGAN, Info-GAN, Text2Image, Puzzle-GAN(이미지 안의 Subpatch들이 존재하여, 이를 활용해 원래 이미지를 복원), CycleGAN(이미지 사이 도메인을 바꿀 수 있는 것), Star-GAN, Progressive-GAN(낮은 이미지를 활용하여 고차원(고화질) 이미지로 바꿔줌)

 ⇒ 처음 설명했던 사이트에 몇 개에 대해서는 설명이 되어 있음

 ⇒ 나중에 시간 날 때 마다 하나씩 찾아보고 정리하는 것을  추천

KL Divergence VS JS Divergence

JS Divergence : https://en.wikipedia.org/wiki/Jensen%E2%80%93Shannon_divergence

KL Divergence, JS Divergence 둘 모두 확률 분포 사이의 유사도를 구하는 것이다.
그렇다면, 왜 2개를 굳이 쪼갠 것일까?

KL Divergence가 두 확률 분포 사이의 유사도를 구하는 방법은 "상대적 정보 손실량의 기댓값"이다.
즉, p와 q가 얼마나 "차이가 존재하는가"에 대해 계산하기 때문에 "-"(minus) 연산이 수행되게 된다.

그런데, 마이너스를 수행하면 한 개의 단점이 발생한다.
바로 Symmetry하지 않다는 것이다
(KL(p || q) != KL(q || p))

즉, 두 확률 분포 사이의 유사도 자체는 구할 수 있지만, 이를 두 확률 분포 사이의 "거리"라고 표시하기에는 무리가 있다
(거리는 p에서 q를 보든 q에서 p를 보든 같은 값을 가져야 함)

따라서, JS Divergence를 활용하는 것이다

JS Divergence는 KL Divergence를 Symmetric하게끔 개량한 것이다.

따라서, JSD(p || q) = JSD(q || p)가 될 것이고, 이러한 이유로 두 확률 분포 사이의 Distance를 구할 때는 KL보다는 JS가 그 역할을 수행하는 것이다

사진 출처
https://deepinsight.tistory.com/126
https://m.blog.naver.com/euleekwon/221557899873
https://parkgeonyeong.github.io/GAN-%EC%A0%95%EB%A6%AC/

DONGJIN IM

개념부터 확실히!

이전 포스트

Generative Model

다음 포스트