Generative Model

Generative Model

주어진 학습 데이터를 통해 학습 데이터의 분포를 따르는 유사한 데이터를 생성하는 모델을 의미한다.

• 종류
  • Explicit Density : 학습 Data 분포에 대한 Model을 확실히 정의할 수 있고, 이를 활용하여 생성하는 Generative Model
  • Implicit Density : 학습 Data에 대한 Model을 정의하지 않고, 확률 분포를 파악하기 위해 Sample을 뽑는 방식

VAE는 대표적인 Explicit Density Model이다. VAE는 Data 분포를 학습할 수 있는 Data에 대하여 Data 분포를 학습하고, Data 분포가 잘 학습된다면 Sampling은 자동으로 수행되는 것이다.
(Sampling : 내가 원하는 Data를 Generative Model을 활용하여 "생성"시키는 것)

GAN은 대표적인 Implicit Density Model이다.
Data 분포에는 큰 관심이 없으며, 단지 진짜 같은 Sample Data를 Generate하는 것을 목적으로 고안된 Sampler이다.

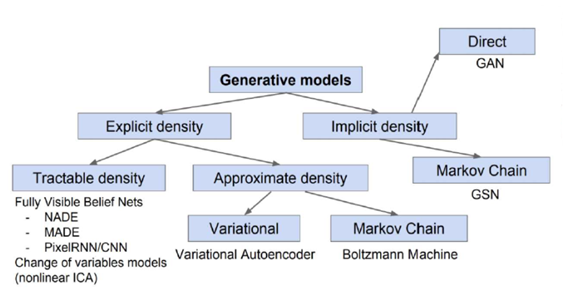
• 출처 : Ian GoodFellow, Tutorial on Generative Adversarial Networks, 2017

Generative Model이 하는 일

Generation

Sampling을 의미한다.
만든 Sampler가 (우리가 원하는) Data를 생성시키는 과정을 수행한다.

Density Estimation

이미지가 주어졌을 때 이미지에 대한 Classification 수행하는 것으로, Anomaly Detection에서 활용된다.

Unsupervised Representation Learning(비지도 학습)

Image들이 공통적으로 가지고 있는 특징을 추출하는 Feature Learning이 수행된다.

Explicit은 Data에 대한 분포를 학습하므로 Density Estimation이 가능하다. 하지만 Implicit은 Data에 대한 분포를 학습하지 않고 단순히 Sampling에만 관심이 있는 Model이므로, Density Estimation은 불가능하다.

알아두면 좋은 수학적 기법

Chain Rule

$p\left(x_1,\ ...\ ,\ x_n\right)\ = p\left(x_1\right)p\left(x_2\ \mid \ x_1\right)p\left(x_3\mid \ x_1,\ x_2\right)\newline \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad...p\left(x_n\mid \ x_1,\ ...\ ,\ x_{n-1}\right)$

Bayes' Rule

Conditional Independence

z라는 상황 아래에서 x와 y가 Independent한 상황임을 가정하자(z가 아닌 상황서는 x와 y는 Independent하지 않을 수도 있다)

수식을 보면, z인 상황에서는 x와 y는 Conditional Independence하므로 고려하지 않아도 된다.
즉, y와 z를 둘 다 만족시킨 상황에서의 p(x)는 z인 상황에서의 p(x)와 동일하다.
따라서 z인 상황에서는 y는 p(x)에 아무런 영향도 끼치지 못하므로 p(x|z)와 동일해진다.

Parameter 계산하기

$p\left(x_1,\ ...\ ,\ x_n\right)\ =\ p\left(x_1\right)p\left(x_2\ \mid \ x_1\right)p\left(x_3\mid \ x_1,\ x_2\right)\newline\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad...p\left(x_n\mid \ x_1,\ ...\ ,\ x_{n-1}\right)$

• Parameter의 총 개수 : $2^n - 1$ 개
  • p($x_1$) : 1 Parameter
  • p($x_2$ | $x_1$) : $x_1$이 0인 상황과 1인 상황 총 2개 상황을 고려해야 하므로, 2개 Parameter가 필요
  • p($x_3$ | $x_1,x_2$) : 4개 Parameter 필요
  • 총 필요한 Parameter 개수 : 1 + 2 + 4 + ... + $2^{n-1}$ = $2^n-1$

위 Case에서는 Parameter 수가 너무 많기 때문에 Model의 Accuracy를 기대하기 어려워지며, 이런 개념으로 볼 때는 Parameter 수를 줄여야 할 필요성이 존재하고, 이를 위해 Conditional Independence를 활용한다.

(ex) Markov Assumption 활용
Markov Assumption : xᵢ₊₁⊥x₁, x₂,...,xᵢ₋₁|xᵢ
즉, (i+1)번째 Data는 i번째 상황에만 Dependent
그렇다면, p(x₁, x₂, ..., xᵢ) = p(x₁)p(x₂|x₁)...p(xᵢ|xᵢ₋₁)이 될 것이다.(Chain Rule & Conditional Independence를 활용하여 나온 수식)

따라서, 필요한 총 Parameter는 1 + 2 + ... + 2 = 2(i-1) + 1 = 2i-1이다.
일반적인 상황에서 2ⁱ - 1이였다는 것을 생각하면 파격적으로 줄어들었음을 알 수 있다

---

기본적인 Generative Model

AR-N 모델

Conditional Independence를 활용하여 Parameter 개수를 줄인 모델로써, 과거 Data 중 가까운 N개 Data만 활용하여 현재 Data를 파악하는 Model이다.

과거 Data를 활용할 때 순서가 매우 중요하므로 Ordering이 필수적인 Model이다.

NADE

• 출처 : https://www.researchgate.net/figure/The-architecture-of-a-Neural-Autoregressive-Density-Estimation-NADE-model-The-input_fig1_332140920

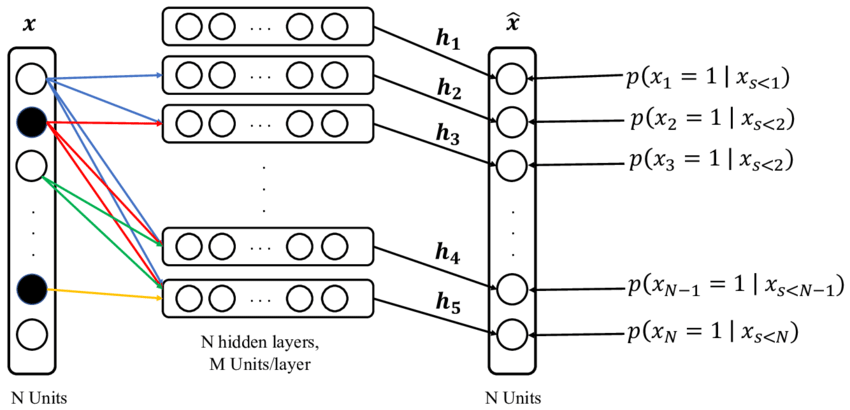
i번째 픽셀은 1 ~ (i-1) 번째 픽셀에 Dependent하다.

i번째 픽셀을 만들 때 먼저 1 ~ (i-1) 번째 픽셀 Data를 받고, 해당 Data를 활성 함수(Sigmoid 사용)에 통과시켜 확률 값을 구한다.
수식을 보면, 1 ~ (i-1) 번째 픽셀을 활용해 $h_i$를 구하고, 해당 값을 또다른 Parameter(Weight)를 활용한 이후 다시 활성함수를 통과시켜 Probability Distribution을 구하는 것을 알 수 있다.
입력 Data 개수가 달라지므로, 계속해서 입력 차원이 달라지며, 가중치 Size도 변경된다.

Explicit한 Model로써, 학습 과정에서 이미 확률 분포를 구했기 때문에, Model의 출력값을 활용하면 Density Estimation이 가능하다.

Output이 Binary Pixel일 경우 활성 함수 Sigmoid 활용하며, Output이 Continuous일 경우 (마지막 Layer에) Gaussian Mixture Model 활용한다.

• Gaussian Mixture Model 설명 : https://untitledtblog.tistory.com/133

Pixel RNN

RGB 색에 대해서, R에 대한 확률 분포를 구하고, 이후 G, B를 앞에서 계산한 값을 통해 순차적으로 확률 분포를 구하는 것이 기본적인 개념이다.
i번째 Pixel을 만들 때 (i-1)번째 Pixel 값을 활용하여 구한다.

(같은 Layer 중) 어느 것도 활용하지 않고 R에 대한 데이터를 구하고, 이전에 계산했던 R을 활용하여 G를 구하며, 이전에 계산했던 R과 G 동시에 활용하여 B를 구하는 식으로 데이터를 형성한다.

Ordering 순서에 따라 RNN 종류가 구분이 가능하다.

• 출처 : https://cvnote.ddlee.cc/2019/08/07/pixel-recurrent-neural-networks

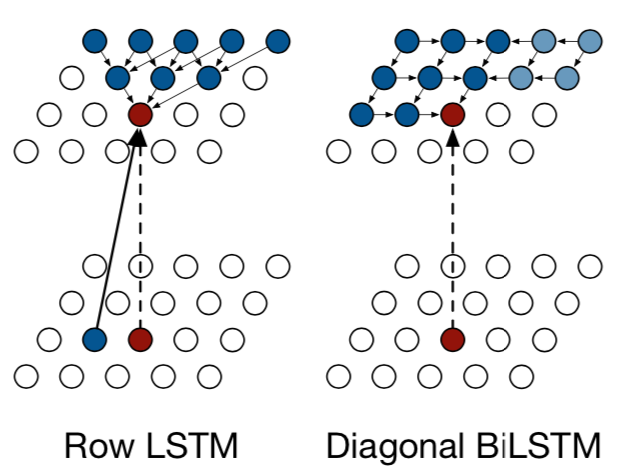
위 사진에서 빨간색 Point가 내가 계산 결과로 도출할 Pixel이고, 파란색 Pixel이 빨간색 Pixel을 만들기 위해 활용하는 Pixel들이다

Row LSTM

같은 Row에 있는 Pixel들과는 전혀 Dependency가 없고, 바로 아래 Layer에서 인접한 3개의 Pixel들을 한번에 가져와 통합하여 계산하는 Model이다.

단, 이렇게만 계산할 경우 모든 픽셀들을 효과적으로 활용할 수 없기 때문에, 직전에 계산된 (같은 Layer에 존재하는) Pixel 결과값을 동시에 활용하여 최종적으로 계산을 수행한다.

Diagonal BiLSTM

지금까지 계산된 모든 Pixel 값들을 모두 활용하는 기법으로, 내가 구하고 싶은 Pixel의 Column 기준으로 왼쪽 Pixel들은 오른쪽 방향과 아래 방향으로 Data를 전파하고, 오른쪽 Pixel들은 왼쪽 방향과 아래쪽 방향으로 Data를 전파한다.

이런 방식으로 Data를 모두 전파하여, 결과적으로 내가 얻고 싶은 Pixel을 구하는 Model이다.