Abstract

• Sample Text로부터 다음 단어를 예측하는 Task를 다룸
• Word의 Class에 기반하여 N-gram Model에 대해 다룰 것임
• 다른 단어와의 동시 발생 빈도(Co-occurence)에 기반하여 클래스를 만드는 통계적 알고리즘에 대해 설명

---

Introudction

왜 이 논문이 나왔는가?

• Noisy Channel을 통과한 왜곡된(Garbled) 단어들을 복구시키는 데 어려움이 존재
  • 이를 해결하기 위하여 어떤 영단어가 Noisy Channel에 들어가는지에 대한 Probability를 예측할 필요성이 대두됨
• 대용량 Text에서 통계적 작용에 의해 Class로 단어를 나누는 것에 대해서도 논의

논문에 대한 간략한 설명

1. 단어를 적절한 Class에 할당하는 것은 계산적으로 힘들기 때문에, Suboptimal Assignment를 찾는 2가지 Algorithm에 대해 설명

2. 2가지 다른 형태의 Word Clustering에 Mutual information을 적용

   • Single Lexical Entity로써 함께 동작하는 단어 쌍을 위해 활용
   • 두 단어가 특정 거리 내에 나타날 확률을 조사하여 Loose Semantic Coherence를 가진 클래스를 찾기 위해 활용

추가 설명

Single Lexical Entity란 어휘 분석을 통해(Lexical) Entity 1개를 찾는 과정이다.
즉, Single Word를 찾는 과정이라고 생각했다.

또한 두 단어가 특정 거리 내에 존재한다는 것은, N-gram Model에서 보았을 때 "얼마나 유사한가"를 나타내는 지표라고 생각한다.
즉, 2개 클래스가 어느정도의 유사성을 가지고 있는지 찾을 수 있다는 것이다.

논문에 들어가기 앞서

• 이 논문은 수학적 이론의 용어와 표기법을 자유롭게 활용함(Draw Freely)
  • 참고로, 이 논문 뿐만이 아닌 다른 논문들도 수학 공식을 약간 자기 입맞에 맞춰 쓰는 경우가 다수 존재하므로, "어떤 의도를 가지고 그 용어를 활용했는가"에 집중하여 수식을 볼 필요가 있는 것 같다.
• 미리 알아야 할 것들
  • Markov Chains
  • Conditional Probabilitis
  • Entropy
  • Mutual Information

Markov Chains

Markov Property부터 알야아한다.
Markov Property는 N번째의 상태가 오직 (N-1)번째의 상태에서만 영향을 받는 것을 의미한다.

Language적으로 Markov Chain을 적용한다면 오직 현재 단어 이전 단어에만 영향을 받아 현재 단어가 형성된다는 것을 의미한다.

Conditional Probabilities

• https://velog.io/@idj7183/DL%EC%9D%84-%EC%9C%84%ED%95%B4-%EC%95%8C%EB%A9%B4-%EC%A2%8B%EC%9D%84-%ED%86%B5%EA%B3%84%ED%95%99-%EC%9D%B4%EB%A1%A0%EB%93%A42#%ED%99%95%EB%A5%A0-%EB%B6%84%ED%8F%AC-%EC%82%AC%EC%9D%B4%EC%9D%98-%EA%B1%B0%EB%A6%AC%EB%A5%BC-%EC%9C%A0%EB%8F%84%ED%95%98%EB%8A%94-%EB%B0%A9%EB%B2%95

Entropy

정보를 표현하는데 필요한 최소 자원량이다.
즉, 정보를 Vector나 2진법등으로 표현할 때, 평균적으로 어느 정도 길이로 표현할 수 있는가에 대한 개념이라고 생각하면 편하다.

Entropy는 "실제 데이터"에 대한 데이터를 활용한다.
예를 들어, 많이 활용되는 단어에는 짧은 Vector를, 적게 활용되는 단어에는 긴 Vector를 활용한다면 전체 문장을 더욱 짧게 표현할 수 있게 되는 것이다.

Mutual Information(KL Divergence)

간단히 말하자면, 두 사건이 얼마나 밀접한 연관을 가지고 있는지 수량화 한것이다.

정확한 의미론적으로 설명하자면, Joint Distribution P(A,B)가 P(A)P(B)와 얼마나 비슷한지를 측정하는 척도로써, KL Divergence 공식에 의해 도출해 낼 수 있다.
(0에 가까울수록 Independent하다. 즉, 연관성이 없다)

KL Divergence는 (크로스 엔트로피) - (엔트로피)이다.
KL Divergence가 작다는 의미는 크로스 엔트로피가 작아진다는 의미이며(엔트로피는 실제 데이터에 대한 값으로 변동이 없음), 이는 내가 예측한 방법으로 만든 엔트로피 값이 작아졌다는 것을 의미한다.
즉, 단어를 Vector로 표시해서 나열했을 때 길이가 더 짧아졌다는 것을 의미하며, 더 효율적으로 구성되었다고 생각하면 된다.

KL Divergence가 작아질수록 A와 B가 유사하다는 의미이며, Mutual Information이 커진다는 것이다.
A가 실제 데이터 분포, B가 우리가 만든 Model이 만든 데이터 분포일 때 MI가 클수록 좋은 모델이라는 의미이다.(왜냐면 두 모델이 가깝다, 즉 차이가 별로 없다는 의미이기 때문에 실제 데이터와 유사하다고 판단해도 문제가 없어지기 때문)

• 0에 가까울수록 Independent한데 작으면 좋다? 무슨 말이죠?

  KL Divergence는 Log 함수를 활용한다. 이 때 log 안에 들어가는 값은 $\frac{p(x_i,y_i)}{p(x_i)p(y_i)}$로써 1 이하의 값을 가진다.
  즉, 0이 가장 큰 값이 되는 것이며, 0 이하가 될수록 Independent가 줄어든다는 것을 의미한다.

---

Language Model

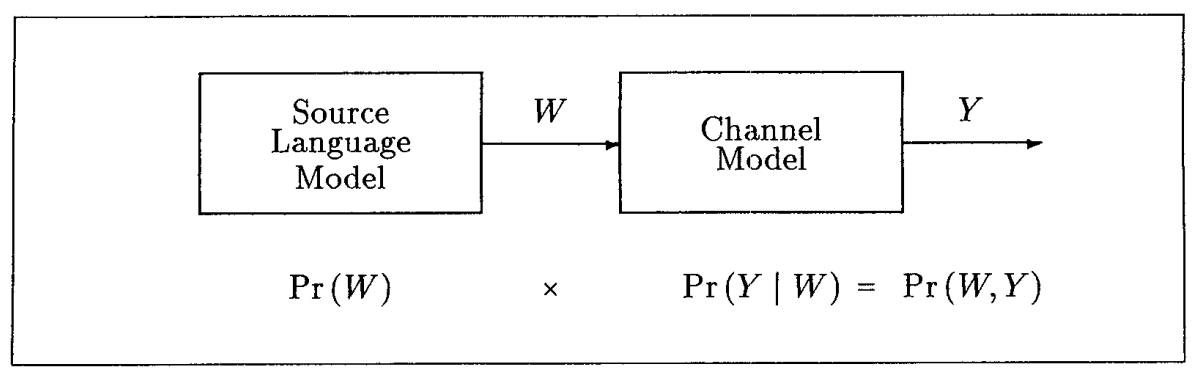
이 논문이 쓰여지게 된 계기

위 사진은 그 당시 활용되던 (Language) Model이다.
Speech Recognition, Machine Translation, Spelling Correction 등의 Task에서 활용되었다.

다른 연구가들은 "결과물 y"에 집중하여 최대한 결과와 가깝게 만들려고 노력하였다.

하지만, 이 논문은 Model의 Input으로 넣어주는 W에 집중하여 성능 향상을 노렸다.

y의 Posteriori Probability를 가장 크게 하는 단어 W를 고르지 않을 Probability Error를 최대한 줄이는 방식으로 학습을 진행하였다.

이게 무슨 말인지 예시를 통해 확인해보자.
내가 원하는 Output은 $y_1$이 나오길 바란다.
하지만, Model의 Input에 따라, $y_2, y_3,...$가 나올 수도 있다.
(어디까지나 Model은 정확한 값을 도출한다기 보다는 확률적으로 가장 큰 값을 결과물로 반환하므로)
즉. $y_1$ 이외의 값이 도출되게 하는 단어 W가 Model의 Input으로 들어갈 확률을 최대한 줄이는 방향으로 학습이 진행된다는 의미이며, Posteriori Probability를 가장 크게 하는 W라는 것은 $y_1$을 도출시키는 단어가 W라는 것을 의미한다.
마지막으로, W를 고르지 않으면 $y_1$이 아닌 다른 값이 도출될 것이므로, 이는 Probability Error의 증가로 이어질 것이다.

Model 관련 수식

• 가정 : 영어 Text는 Conditional Probabilities로 특정 할 수 있음

  • 원래라면 The cat sat 라는 단어 이후에 어떤 단어가 올지 "영문학적 정의"로써는 정할 수 없다. 왜냐하면 The cat sat이 문장의 끝일지, 아니면 이후 장소가 나올지는 영문학적 정의에서는 알 수 없는 내용이기 때문이다.
    하지만, 이 논문에서는 The, cat, sat이라는 단어를 활용하여 Conditional Probabilities를 구하면 "on"이라는 단어가 이후 나올 확률이 가장 높다는 것을 반환할 수 있으며, 이 단어로 특정 지을 수 있다는 가정을 가지는 것이다.

• 용어 설명

  • $w_1^{k-1}$ : 1 ~ (k-1) 번째까지의 단어

수식 설명

N-gram을 대표하는 수식이라고 할 수 있을 것이다.
1 ~ k번째 단어 w가 순서대로 나올 확률이 $Pr(w_1^k)$이다.

위 가정에서 영어 Text는 Conditional Probabilities로 특정 가능하다고 했다.
즉, $w_1$이 나올 확률은 $Pr(w_1)$이며, $w_1$ 이후 $w_2$가 나올 확률은 $Pr(w_2|w_1)$가 될 것이다.

우리는 "동시에" $w_1 \sim w_k$까지 나올 확률을 구하고 싶기 때문에 위에서 구한 모든 Pr값을 곱해줘야 할 것이다.
(왜냐면 $w_1$이 나오고, 동시에 이후 단어가 $w_2$여야 하며, 동시에 이후 단어가 $w_3$여야 하는 과정이 반복되므로)

위 과정을 통해 수식을 도출할 수 있다.

결과 측정 방법

• 완벽한 System의 Context와 우리가 만든 Model의 예측치를 비교하는 것은 너무 많은 비용이 소비됨

  • 이를 대체할 수 있는, 본질적인 측정치 방법이 필요함

• 이 논문에선 결과 측정을 위해 "Perplexity"라는 것을 활용함

Perplexity(PPL)

언어 모델을 평가하기 위한 내부 평가 지표이다.
즉, 2개의 언어 모델(Language Model;LM)이 존재할 때 이 2개를 비교할 방법이 필요한데, 만약 결과물의 완성도로 비교하면 위에서 말한 것처럼 너무 많은 비용이 소비 될 것이다.
따라서 활용하는 방식이 PPL이다.

여기서 중요한점은 PPL은 낮을수록 모델의 성능이 좋다는 점이다.
(나중에 나오겠지만, 역수를 취해주기 때문)

PPL은 단어의 수로 정규화 된 Test Data에 대한 확률의 역수이다.
(논문에서는 기하학적 평균의 역수라고 표현)

문장 W의 길이가 N이고, 문장 W의 i번째 단어를 $w_i$라고 하자.
이 때 PPL 수식은 아래와 같다.
$PPL(W) = P(w_1, w_2, ... w_N)^{-\frac{1}{N}}=\sqrt[N]{\frac{1}{P(w_1, w_2, ... w_N)}}$

위 수식에 Chain Rule을 적용하면 아래와 같이 변경된다.
$PPL(W) = \sqrt[N]{\frac{1}{P(w_1, w_2, ... w_N)}} = \sqrt[N]{\frac{1}{\Pi_{i=1}^NP(w_i| w_1, ... w_{i-1})}}$

논문에서는 Perplexity는 Sampling Error의 영향을 받으므로 언어 모델 간 미세한 차이에 대해서도 측정된다고 말하고 있다.

그렇다면 N-gram Model에서의 Perplexity는 어떻게 될까?
N-gram Model은 $Pr(w_k | w_1^{k-1})$과 $Pr(w_k|w_{k-n+1}^{k-1})$을 동일하게 본다.
(N-gram Model은 "이전 N개 단어"만 현재 단어를 예측하는데 활용하기 때문)

즉, $PPL(W) = \sqrt[N]{\frac{1}{\Pi_{i=1}^NP(w_i|w_{k-n+1}^{k-1})}}$

Parameter 개수

1-gram Model은 $Pr(w)$ 값만 존재하면 되기 때문에, Parameter 개수는 총 (V-1)개가 될 것이다.
원래라면 V개의 단어가 존재하므로 Parameter 개수는 V라고 생각할 수도 있지만, Probability를 모두 합치면 1이 되야한다는 조건 때문에 (V-1)개 Parameter가 필요하다는 제약조건이 있다고 한다.
(나머지 1개에 대한 Parameter는 그냥 1 - (나머지 Pr값)을 통해 계산할 수 있으므로)

2-gram Model은 $Pr(w_{k}|w_{k-1})$ 값이 필요하기 때문에, 총 V(V-1) Parameter가 필요할 것이다. 또한, 2-gram Model에도 $Pr(w_k)$는 필요할 것이므로 Pr(w)의 Parameter 총합은 $V(V-1) + (V-1) = V^2-1$이다.

이처럼 연산을 이어나가면, n-gram Model에서는 $V^{n-1}(V-1) + (V^{n-1}-1) = V^{n-1}-1$만큼의 Parameter가 필요할 것이다.

Sequential Maximum Likelihood estimation

이 논문에서 Parameter 평가 방법으로 활용되는 방법을 말한다.
간단히 말하자면, order-n parameters Model에서 Train 과정에 어떤 방식으로 학습이 일어나는지에 대한 수식이라고 생각할 수 있다.

• 용어 설명
  • C(w) : 1 ~ T까지의 Sentence에서 단어 w가 등장한 횟수
  • $C(w_1^{n-1}w_n)$ : $w_1 \sim w_{n-1}$까지의 단어가 나왔을 때, 다음 단어가 $w_n$인 횟수

위 수식은 Train 과정에서 활용되는 함수라고 말하였다.
그렇다면 어떻게 활용될까?

우리는 $w_1 \sim w_{n-1}$ 단어가 나왔을 때 이번 단어를 $w_n$으로 예측하고 싶은 것이다.
즉, $Pr(w_n|w_1^{n-1})$을 최대화 시키는 방향으로 Model의 학습이 진행되는 것이다.

Interpolated Estimation

대충 예상하다시피, N-gram에서 N이 커질수록 Accuracy 자체는 더욱 커질 것이다.
하지만 Parameter의 수식을 보면, N이 커질수록 Parameter의 개수도 기하급수적으로 커짐을 알 수 있다.

즉, N의 증가는 Accuracy의 증가를 가져오지만, 데이터가 충분하지 않다면 Reliability가 떨어지며, 필요한 데이터의 개수도 기하급수적으로 늘어날 것이다.

이를 해결하기 위한 방법이 Interpolated Estimation이다.

이 방법을 간단히 설명하자면, "여러 LM을 Linear하게 일정 비율로 섞는 것"이라고 할 수 있겠다.

수식으로 이해하자

• 용어 설명
  • $\hat{Pr}$ : 최종적으로 활용할 모델
  • $Pr^{(j)}$ : j-gram Model에서 구하는 (N-gram 기반) 확률
  • $\lambda_j$ : Probability를 최대화하기 위해 각 모델에 가중치를 주는 held-out data

즉, Interpolated Estimation은 1-gram ~ j-gram Model을 일정 비율로 곱해준 이후 합해주는 것이다.

이 논문에서는 j를 3까지, 즉 1-gram, 2-gram, 3-gram Model을 통합시켜 최종 모델을 형성하는 것에 대해서 설명하고 있다.

---

Word Classes

단어는 유사성을 가지고 있다.
만약, 그 유사성을 활용해 단어들을 Class로 묶으면 더 좋은 예측이 가능하지 않을까라는 생각으로 나온 개념이다.

단어에 Class를 적용하기

클래스를 활용한 N-gram Model의 수식은 위와 같을 것이다.
$w_k$를 예측할 때 원래는 $w_1 \sim w_{k-1}$을 활용했지만, 우리는 클래스를 활용하기로 했다.
따라서 Word들을 Class로 치환하면 $Pr(c_k|c_1^{k-1})$가 될 것이다.
마지막으로 우리는 "Word"를 예측하고 싶은 것이다.
따라서, $Pr(w_k|c_k)$를 곱해주어, 해당 클래스 중 특별히 우리가 원하는 단어일 확률을 구하는 마지막 과정이 수행되어야 한다.

위 수식에 대한 Parameter 개수를 구해보면, 총 $C^n - 1 + V - C$개임을 알 수 있다.
이는 단어에 대해서만 N-gram을 수행했을 때보다 훨씬 적은 개수의 Parameter라는 것을 알 수 있다.

Class를 활용한 학습 방향

• 용어 설명
  • $\pi$ : 단어를 Class로 Mapping해주는 함수
  • C(c) : 1 ~ T까지 나온 단어 중 Class C인 단어들의 개수

• 수식 설명
  • 1 $\Rightarrow$ 2
    수식적인 이해보다는 개념적으로 접근했다. 우리가 구하고 싶은 것은 단어 $w_1$이후 $w_2$가 나오는 횟수와 $c_1$이후 $c_2$가 나올 확률, 그리고 $c_2$ 안에 $w_2$일 확률을 Log 연산을 통해 구해주는 것이다.
    이를 풀어서 생각하면, 먼저 현재 클래스가 $c_2$일 확률을 구하는데, 이때 $c_1$ 이후에 $c_2$가 나와야 하므로, $c_1$ 이후 $c_2$가 나올 확률 & $c_2$가 나올 확률을 곱해준다. 마지막으로, 2개 클래스가 연속으로 나오는 개수를 세준다.
    즉, 앞 수식은 클래스 $c_1$ 이후 $c_2$가 나오는 것에 관련된 수식이다.
    다음으로 우리는 $w_1$ 이후 $w_2$가 나올 확률을 구해주고 싶을 것이다. 먼저, 현재 과정에서 $c_2$가 나오고, 해당 Class 중 $w_2$가 나올 확률을 곱해준다.(동시 사건이므로)
    마지막으로, $w_2$ 이전에 나오는 모든 단어에 대한 합연산을 진행하여 모든 단어 Case에 대한 연산을 수행한다.
    즉, 여러 개 단어 Case에 대하여 이번 클래스가 $c_2$이고, 해당 클래스 중 $w_2$가 뽑힐 확률을 구한다. 그런데 하필이면 앞 단어가 Class $c_1$에 속하는 확률을 구해 결국 $w_1$이 속하는 $c_1$ 다음 $c_2$에 속하는 $w_2$가 나오는 연산이 진행되는 것이다.
  • 2 $\Rightarrow$ 3
    $logPr(w_2|c_2)Pr(c_2)$는 결국 $Pr(w_2)$이다. 또한, $\frac{\sum_wC(ww_2)}{T-1}$은 $w_2$의 Frequency와 관계 있으므로, $Pr(w_2)$로 간주할 수 있다.
    마지막으로 $w_2$는 고정되어 있지 않으므로(전체 단어가 후보이므로) w로 치환 가능하니 앞 수식을 형성할 수 있다.
    $Pr(c) = \frac{C(c)}{T}$이므로 $\frac{C(c_1c_2)}{T-1}$도 비슷하게 $Pr(c_1c_2)$로 치환 가능하며, 최종 수식이 만들어진다.

자, 다음 Step을 이해하기 전 위 수식이 이해가 안된다고 해도 걱정하지 말자.
수학을 알고 있는 사람일 수록 헷갈릴 수 있는 수식인 것 같다.
상수항은 도대체 어떻게 없앴으며, 비례한다고 같다고 처리하는 것은 어디서 나온 생각인지 궁금할 수 있다.
하지만 위에서 말했듯, 이 논문은 "자기 맘대로" 수식을 활용한다.
즉, 수식의 정확도를 따지기 보다는 어떤 의미로 이렇게 수식을 변형시켰는지 확인하자.

한마디로, $w_1$이후 $w_2$가 나올 확률을, $c_1$ 뒤에 $c_2$가 나올 확률을 구하고, 이 중 특별히 $c_2$에 존재하는 다양한 단어 중 딱 $w_2$일 확률을 구하여 두 개를 조합한 수식이라고 생각하면 된다.

마지막 수식에서 H(w)는 1-gram Word Distribution의 Entropy이며, $I(c_1, c_2)$는 인접한 Class들의 평균 Mutual Information이다.

우리는 $L(\pi)$를 최대화 시키기 원하기 때문에, 결국에는 $I(c_1, c_2)$을 최대화 시켜야 한다.

Mutual Information 최대화

위에서 말했듯 우리는 Mutual Information을 최대화 시켜야 한다.
하지만, 이렇게 Partition을 만드는 실용적인(Practical) Method는 존재하지 않으므로, Greedy Algorithm을 활용할 것이다.

Greedy Algorithm은 아래와 같은 순서로 진행된다.
1. 단어를 Distinct Class에 할당함
2. 인접 클래스 사이에 Average Mutual Information을 계산
3. 최소 값을 가진 2개 Group을 하나로 합침
4. 1 ~ 3 과정을 (V-C)번 수행하면 총 C개 Class만 남음

여기서 발생하는 문제점은, 한 단어가 Class에 한번 들어가면 다른 Class로 못들어간다는 점이다.
따라서, Merge 시킨 이후 Average Mutual Information 값이 가장 큰 Partition에 들어가 Cycle을 돌며, 해당 단어를 다른 Partition에 넣어보며 그럼에도 불구하고 우리가 선택한 Partition이 가장 큰 Mutual Information 값을 가지는지를 확인한다.
만약, 이 과정을 거쳤는데도 해당 클래스가 가장 큰 Average Mutual Inforamtion 값을 가진다면 잘 Partition 된 것이라고 볼 수 있다.

위와 같은 알고리즘으로 수행한 결과, 놀라울 정도의 Grouping 결과를 보였다
특히, 없는 단어에 대해서는 Mistype으로 간주하여, Mistype의 원본 단어와 매우 유사하다고 Partition(Class)로 묵였음을 볼 수 있었다.

---

Sticky Pairs and Semantic Classes

Sticky

인접한 단어 $w_1$과 $w_2$에 대한 Mutual Inforamtion에 대한 수식이다.
대부분 $w_1$과 $w_2$는 다른 단어와도 결합될 수 있으므로 $Pr(w_1w_2)$ 값이 더 작고, log 값도 음수가 나온다.

하지만 가끔 $Pr(w_1w_2)$이 더 커서 양수가 나오는 경우가 있다.

이런 Case를 Sticky라고 할 것이며, Symmetric 하다는 특징을 가지고 있다.

• Sticky에 대한 예시

  예를 들어, New York 이라는 단어는 이상하게 많이 쓰일 것이다(당연하다. 우리가 알다시피 저 단어는 저 2개 단어를 합쳐 하나의 Entity로 활용되니깐)
  하지만 Model 입장에서는 New York이 도시인지, 새로운 York인지 알 도리가 없다.
  이런 상황에서 위 log 수식을 계산해보면 New York는 양수의 Mutual Information 값을 가지며, 이를 통해 Model은 New York이 사실 한 단어라는 것을 알게 된다는 것이다.

• Sticky가 Symmetric하다고요?

  생각해보자.
  New York는 New 다음 York가 나오기 때문에 Sticky 한 것이다.
  만약 York New라는 단어가 나온다면 이 또한 Sticky로 볼 수 있을까?
  아마 아닐 것이다.(이런 Entity는 내가 아는 한 존재하지 않으므로)
  즉, Sticky는 Symmetric하다는 것이다.

Semantically Sticky

• 수식 이해 : $Pr_{near}(w_1w_2)$
  • $w_1$를 중심 단어로 설정했을 때, 5보다 먼 거리에서 랜덤하게 뽑힌 (가까운) 1001개 단어를 Select했을 때, $w_2$일 확률을 의미함
  • 즉, 좌우로 500개씩 단어를 고르는데, 여기서 $w_1$가 가까운 5개 단어씩을 빼야하니깐(자기자신 포함) 왼쪽에서 495, 오른쪽에서 495개 단어 중 하나를 선택했을 때 이 단어가 $w_2$일 확률을 의미함

$Pr_{near}(w_1w_2)$이 $Pr(w_1)Pr(w_2)$보다 크다면 Semantically Sticky라고 한다.

이는 "의미적으로" 유사한 단어라는 것을 말한다. 즉, 유사한 단어는 가까운 위치에서 다시 사용되었을거라는 생각으로 위와 같이 지정해준 것이다.
위 수식을 통해 Semantically Sticky한 단어들을 구하면 {we, our, us, ourselves, ours} 등으로 묶여 의미적으로 비슷한 의미를 가짐을 알 수 있다.

또한, Semantically Sticky는 Sticky와는 다르게 Symmetric하다
(we - our는 유사하고, our - we 또한 의미론적응로 유사하다)

---

Discussion

저자들은 이 논문으로 (단어 표현에 있어서) 통계적 기술의 가치를 보여줬다고는 생각하지만, 완전한 가치를 입증하지는 못했다고 말했다.

Word Classes를 활용하면 Perplexity 자체는 조금 커지지만 저장 공간을 상당히 Save할 수 있어 더욱 실용적이 된다고 말한다.

저자들은 이 논문에 나온 기법을 활용했지만, 그렇게 큰 성능 향상을 보지는 못했다.
하지만, 3-gram Model이 더 좋은 성능을 낼 때 이 논문이 결국에는 큰 도움이 될 것이라는 것에 대해 자신감을 가지고 있다.

---

느낀점

내가 지금까지 본 논문 중 가장 오래된 논문이라 그런지 정리하기가 조금은 힘들었다
(내가 소주제를 직접 정해야 하는 느낌...?)
또한 이 논문을 읽을 때 미리 알아두면 좋을점을 써둔 논문이라 꽤나 신박했던 것 같다
또 다른 논문들은 SOTA를 달성했다고 무조건 써 놓던데, 솔직히 성능을 못냈다는 부분을 마지막 Discussion에 추가한 것도 꽤 신박하게 느껴졌었다.

N-gram이라는 기법이 사실 이전 N개의 단어만 활용한다는 것만 알고 모호했던 것 같은데 이 논문을 통해 조금 더 확실히 알게 된 것 같은 경험이였다.