기계 학습(Machine Learning)

• 사진 출처 : https://opentutorials.org/module/4916/28942

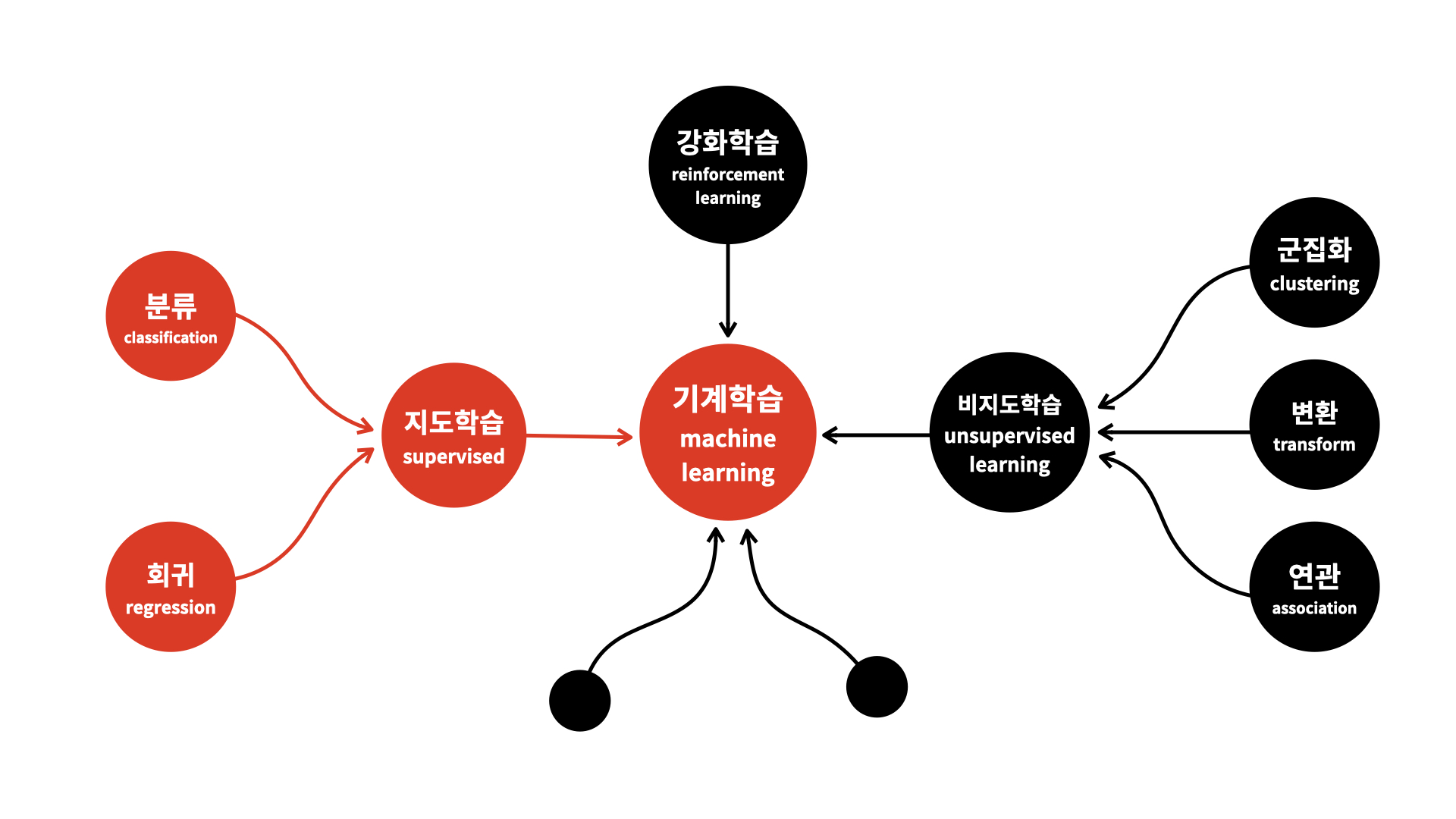
Unsupervised와 Supervised

먼저 Unsupervised와 Supervised의 차이를 알 필요가 있다.

한 마디로 설명하자면,
Unsupervised는 Labeling 없는 Data로 학습하는 것, Supervised는 Labeling한 Data로 학습하는 것이다.

Supervised Learning은 쉽게 이해가 될 것이다. "나는 우울해"라는 문장에 "슬픔"이라고 Labeling한 데이터를 활용하여 모델의 학습을 진행하는 것이다.
즉, 모델이 맞춰야 할 답이 존재하는 것이기 때문에 Loss를 구하고 모델이 학습되는 과정이 쉽게 이해가 된다.

하지만 Unsupervised Learning은 이해가 잘 가지 않을 수 있다.
어떻게 정답이 없는데 학습을 진행할까? "나는 우울해"라는 문장만 주어졌을 때 도대체 이 문장으로 어떻게 학습을 진행하면 될까?

유명한 모델 중 하나인 BERT를 예시로 들어보자.
BERT는 먼저 Large Corpus에 대하여 Unsupervised Learning을 수행한다(자세한 것은 나중에 배운다)
어떤 방식으로 진행 된냐면, 문장이 주어졌을 때 특정 단어를 [MASK]로 치환하고, 해당 부분의 단어를 예측하는 방식으로 학습이 진행된다.
예를 들어, "나는 오늘 밥을 먹었다"에서 "나는 오늘 [MASK] 먹었다"라는 문장으로 바꾸고, [MASK] 단어를 맞추는 방식으로 학습이 진행되는 것이다.
"나는 오늘 밥을 먹었다"에 대한 정답 Label은 없지만, [MASK]를 맞추는 과정에서 학습이 진행된다.

다른 예시로는 Word2Vec이 있을 것이다.
Word2Vec은 텍스트를 집어 넣어 단어를 Vector로 바꾸는 알고리즘이다. 이 과정에서 텍스트(Corpus)에 대하여 어떠한 Labeling도 수행되지 않으며, 그럼에도 불구하고 비슷한 단어들은 비슷한 벡터 공간에 존재하게 되는 방식으로 학습이 진행된다.

Unsupervised Learning 종류

1. Clustering
비슷한 것을 묶는 Unsupervised Learning을 말한다.
다른 말로, 한 개의 큰 그룹을 작은 그룹으로 세분화하는 알고리즘이다.

대표적인 예시로 K-means Clustering이 존재한다.
클러스터(Cluster)라고 부르는 2개의 중심점을 알맞은 자리에 위치시키고, 이 중심점을 바탕으로 데이터를 2개로 군집화하는 것이다.
A점과 B점을 중심점으로 지정하였을 경우, A점을 중심으로 하는 A Set Data, B점을 중심으로 하는 B Set Data로 나누어 2개의 Data 그룹으로 만들게 된다.
이렇게 만들어질 2개 Data가 최적으로 나누어지는 지점을 찾는 것이 K-means Clustering의 특징이다.

2. 데이터 압축(Dimensionality Reduction)
다차원의 데이터를 한 단계 낮은 차원의 데이터로 축소하는 방법을 말한다.
데이터 압축을 수행하면 머신이 학습하는 시간을 단축할 수 있으며 동시에 성능이 좋은 시스템을 빠르게 구축할 수 있게 된다.
(차원의 저주 문제를 해결할 수 있는 대표적인 방법 중 하나이다)

3. 연관 규칙 학습(Association Rule Learning)
어떤 사건이 얼마나 자주 함께 발생하는지, 혹은 얼마나 연관되어 있는 분석하는 것이다.
예를 들어, A라는 특징을 가지고 있는 사람들은 B라는 특징도 가지고 있는 추세를 보인다 라는 관계성을 찾는 알고리즘이다

Supervised Learning 종류

1. 분류
데이터를 특정한 Label들로 나누는 것을 의미한다.
Clustering과 다른 점은 분류(Classification)은 쪼개지는 Label 값이 정해져있지만 Clustering은 그렇지 않다는 점이다.

대표적인 알고리즘으로 SVM 알고리즘이 존재하는데, 데이터 속성 간 Decision Boundary라고 부르는 Hyperplane을 그려 Margin을 최대화하는 Hyperplane을 구하는 알고리즘이다.
데이터는 이미 Labeling이 되어 있으며, 단지 Labeling된 Data를 최적으로 쪼개는 Hyperplane을 구하는 알고리즘이므로 Classification이 될 것이다.

2. 회귀
특성(Feature)를 기준으로 연속된 값을 예측하는 것을 말한다.
Labeling 처럼 옳고 그름, 혹은 특정 숫자로 결과가 나오는 것이 아닌 실수값으로 결과가 나오는 경우를 말한다.

대표적인 예시로 Linear Regression 알고리즘이 존재한다.
Input Data x를 최대한 Linear하게 만들기 위해 데이터 x를 변환시켜 y로 만드는 알고리즘이다.

이 회귀는 결국 Input Data x를 y로 변환시키기 때문에 Unsupervised가 아닐까 생각할 수도 있다.
하지만 중요한 점은 Linear Regression 과정은 Y라는 종속 변수가 존재한다는 것이다.
결국 Input Data x에 대해서 Y라는 예측치가 나와야하기 때문에 Labeling을 미리 수행한 것이고, $(x_1, y_1), (x_2, y_2), ...$을 최대한 선형으로 만들기 위해 데이터를 변환하는 것으로, Supervised Learning이라고 할 수 있을 것이다.

• 예시로 본 회귀와 분류
  특정 문자가 욕인지 아닌지를 살펴본다고 하자.
  이 때, 답은 "욕이다", 혹은 "욕이 아니다" 2개 Label만 존재하므로, 분류 문제가 된다
  땅 위치, 주변 편의 시설 등의 Input이 주어졌을 때 땅값을 예측하는 문제를 풀어보자
  이 때 결과는 "숫자"로 나오게 될 것이다. 하지만, 해당 Input에 대하여 "300만원" 등의 Label 값은 존재한다.
  따라서 이런 문제는 회귀 문제라고 생각할 수 있을 것이다

분류 문제에서는 선형 회귀를 활용하지 않는 이유

• 공부한 사이트 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=je1206&logNo=220783024411

정확히 말해서는 "할 수 있지만 권장하지 않는다"가 맞는 말이다.

회귀 문제에서 중요한 점은 "Label의 값에 의미가 존재하지 않는다"이다.
하지만, 선형 회귀 같은 경우 Output이 값으로 나오게 된다.
예를 들어, Labeling이 1, 2, 3일 때 Output이 1.5라면, 이 값은 어떤 Label에 포함될까?

그럼 Label이 2개이고 Output을 0 ~ 1로 두어 Probability로 구하면 되지 않을까? 여기에서도 문제가 존재한다.
"선형"이라는 것을 생각해보면, 이 선형 값에는 Label을 넘어가는 값(즉, 1 이상)과 Label보다 작은 값(즉, 0 이하)도 존재하게 된다.
그런데 어쨌든 선형 회귀 모델에서는 Output으로 나올 수 있기 때문에
분류 문제에서도 해당 Answer를 확률에 포함시킬 것이다.
즉, 절대로 나올 수 없는 값을 확률에 포함시키기 때문에 Accuracy가 떨어진다.
이를 위해 활용하는 모델이 "로지스텍 회귀 모델"이다.

Logistic Regression

로지스틱 회귀는 Linear Regression의 확률화라고 생각하면 편하다

데이터를 Linear Regression을 통해 변환해본다.
이 때 위에서 말했듯 0 ~ 1 사이 값이 아닌 음수 및 1 초과인 수도 많이 나오게 될 것이다.
이 함수를 정제하여 0 ~ 1 사이 값을 가지게 하고, 이를 확률로 보아 그 중 최대 값을 가진 Label으로 Classification 문제를 해결할 수 있을 것이다.

0 ~ 1 사이 값을 가지게 하는(이진 분류 모델 Case) 가장 대표적인 함수는 Sigmoid 함수이다.
또한 다중 분류 모델의 경우 0 ~ N 사이의 값을 가져야 할텐데, 이 경우에는 Softmax 함수를 활용한다.

코드로 간단히 구현한 Logistic Regression

class BinaryClassifier(nn.Module):
    def __init__(self, in_features):
        super().__init__()
        self.linear = nn.Linear(in_features, 1)
        self.sigmoid = nn.Sigmoid()
    def forward(self, x):
        return self.sigmoid(self.linear(x))

Sigmoid Layer를 거쳐 0.5 이상이라면 1으로 예측하여 "맞다"라고 판단하고, 0.5 미만이라면 0으로 예측하여 "틀리다"라고 판단하는 것이다.

만약 다중 분류를 수행하고 싶다면, nn.Linear의 1을 Class 개수로 바꾼 뒤 nn.Sigmoid()가 아닌 nn.Softmax(dim=1)를 활용하면 될 것이다
([x,y]에서 x는 Batch Size를 의미하므로, dim=1으로 설정해 줘야 한다)

사이킷런을 활용한 (단일, 다중) 분류 회귀분석 코드

from sklearn.linear_model import LogisticRegression

model = LogistricRegression(C=20, max_iter=1000)
lr.fit(train_data, train_target)
# 이 부분에서 다중 분류를 설정할 수 있다.
# train_target에 N개의 Class가 저장되어 있다면 다중 분류가 수행될 것이다
# 반대로, 2개 Class만 존재한다면 0 혹은 1로만 분류할 것이다

lr.predict(train_data)
# train_data를 통해 예측한 값

lr.predict_proba(train_data)
# train_data를 통해 얻은 정답 확률

• max_iter : 모델 훈련 반복 횟수
  • 최소값 : 100
• C : 규제 정도
  • alpha와 같은 기능을 수행한다.
  • alpha : 값이 커지면 규제 정도가 세짐
    C : 값이 작을수로 규제 정도가 세짐
  • 나중에 Overfitting을 줄이는 방법에서 자세히 설명하겠다.

lr.predict_proba를 통해 얻은 확률을 활용해 가장 큰 확률을 가진 Label으로 예측하는 것이고, 이를 lr.predict를 통해 출력할 수 있는 것이다.

참고로, train_target에서 입력되어 있는 Class 순서가 어떻든 알파벳순으로 정렬하여 활용한다.

따라서, print(lr.classes_)를 통해 Index에 해당하는 Class Name을 미리 파악하는 것을 추천한다.

여기서 (내 기준으로) 매우 신기한 기능이 있었으니, 바로 lr.coef_이다.

lr.coef_는 계수(coefficients)를 확인하는 메서드인데, 이 값을 출력함으로써 어떤 Feature가 결과에 큰 영향을 주는지 확인할 수 있다.

예를 들어보자. Input Data의 Feature가 ['Sex', 'Age', 'FirstClass', 'SecondClass'] 순으로 입력되었다고 가정하자.
그리고 coefficients가 [1.22434276 -0.42234411 0.99546021 0.43311383]로 출력되었다고 가정하자.

그렇다면 우리는 Coefficients 값을 통해 어떤 Feature가 생존이라는 결과에 영향을 미치는지 알 수 있다.
Sex는 1.22의 값을 가진다. 즉, Sex는 양수의 값을 가진다. 따라서, 성별이 1(즉, 클 수록)으로 설정될수록 생존확률이 올라간다는 것을 알 수 있다.
또한, 'FirstClass'가 'SecondClass'의 계수보다 크다. 따라서 FirstClass에 탑승했다면 생존확률이 올라갔다는 것으로 이해할 수 있다.
마지막으로, Age는 음수의 값을 가지므로 나이가 많을수록(수가 클수록) 생존 확률은 낮아진다고 파악할 수 있다.

---

선형 회귀(Linear Regression)

선형 회귀란?

종속 변수 y와 1개 이상의 독립 변수 x와의 선형 관계를 모델링하는 회귀 분석기법이다.
회귀 분석이란 둘 이상의 변수 간의 관계를 보여주는 통계적 방법으로 이해하면 될 것이다.

즉, 여러 개의 데이터가 있을 때 선형 관계를 가지도록 데이터를 변환해주는 기법이다.

선형 회귀의 종류

• 단순 선형 회귀 분석(Simple Linear Regression Task)
  $y=Wx+b$
  • 독립 변수 1개에 의하여 종속 변수를 도출 하는 선형 회귀 방식
• 다중 선형 회귀 분석(Multiple Linear Regression Analysis)
  $y=W_1x_1 + W_2x_2 + ... + W_nx_n+b$
  • 독립 변수 N개에 의하여 종속 변수를 도출 하는 선형 회귀 방식

선형회귀식 찾는 방법

1. 무어 펜로즈 역행렬

• 수행 과정
  (1) y = bx에서 b를 찾고 싶다.
  (2) Xb = y => b = X$^+$y( X$^+$ : 무어 펜로즈 역행렬)
  (3) X$^+$는 Python에서 np.linalg.pinv(X)를 통해 구할 수 있으므로, b도 구할 수 있음
  

2. 경사 하강법
최근에는 무어 펜로즈 역행렬 보다는 경사 하강법을 많이 활용하기 때문에, 수행 과정을 잘 알아야 한다.

다음 Section의 핵심이라고 볼 수 있다.