Gradient Descent

DONGJIN IM·2022년 4월 25일

AI 이론

AI(NLP) 이론

목록 보기

2/18

선행되어야 할 개념들

Loss Function(Cost Function)

모델은 y = Wx+b를 가장 잘 만족시키는 W와 b를 찾을 것이다.
그렇다면 어떻게 해야 W, b가 적절한 값인지 판별할 수 있을까?

이를 위해 Cost Function(Loss Function)이라는 것을 활용한다.

결론부터 말하자면 내가 만든 Model의 예측 값과 실제 값을 비교하여 나오는 차이를 Loss라고 생각하고, 이 Loss를 함수식으로 형성하여 Loss Function을 생성하는 것이다
우리는 Loss를 최소화 하는 것을 원하기 때문에, 결국 Loss Function을 최소화 시키는 W와 b를 찾으면 되는 것이다.

예를 들어, Wx+b를 통해 예측한 값이 y'이고, 실제 x에 대한 값이 y일 때 ||y-y'||을 가장 작게 만드는 W와 b를 찾는 것이라고 말할 수 있을 것이다

그렇다면 어떤 방법으로 최적의 W와 b를 구할 수 있을까?
바로 이를 위해 활용되는 것이 Optimizer이다.

Optimizer(최적화 알고리즘)

모델의 Loss Function을 최소화 하는 W, b 등의 Parameter를 찾기 위해 활용되는 알고리즘으로, $||y-y'||$ 을 최소화 시키는 Parameter를 찾기 위해 활용되는 "방법"을 Optimizer라고 한다.

경사 하강법은 대표적인 Optimizer 중 하나이다.

경사 하강법

경사 하강법이란?

미분 값을 빼서 함수의 극솟값의 위치를 구할 때 활용하는 방법이다.

미분값을 더하여 함수의 극댓값의 위치를 구할 때 활용하는 방법인 경사 상승법이 존재하는데, 이와 반대되는 개념이라고 할 수 있다.

우리는 Loss Function의 "극솟값"을 찾기 원하므로 경사 하강법을 활용하며, 만약 Function이 다변수로 확장될 경우에는 Gradient Vector를 활용한다.
Gradient Vector란 변수별로 편미분하여 계산한 Vector로써, 수식은 아래와 같다.

$\nabla f = (\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, ..., \frac{\partial f}{\partial x_n})$ : Gradient Vector

Optimizer(with 경사 하강법)

다른 Optimizer도 다양하지만, 여기서는 경사 하강법을 활용하는 Optimizer들만 설명하겠다

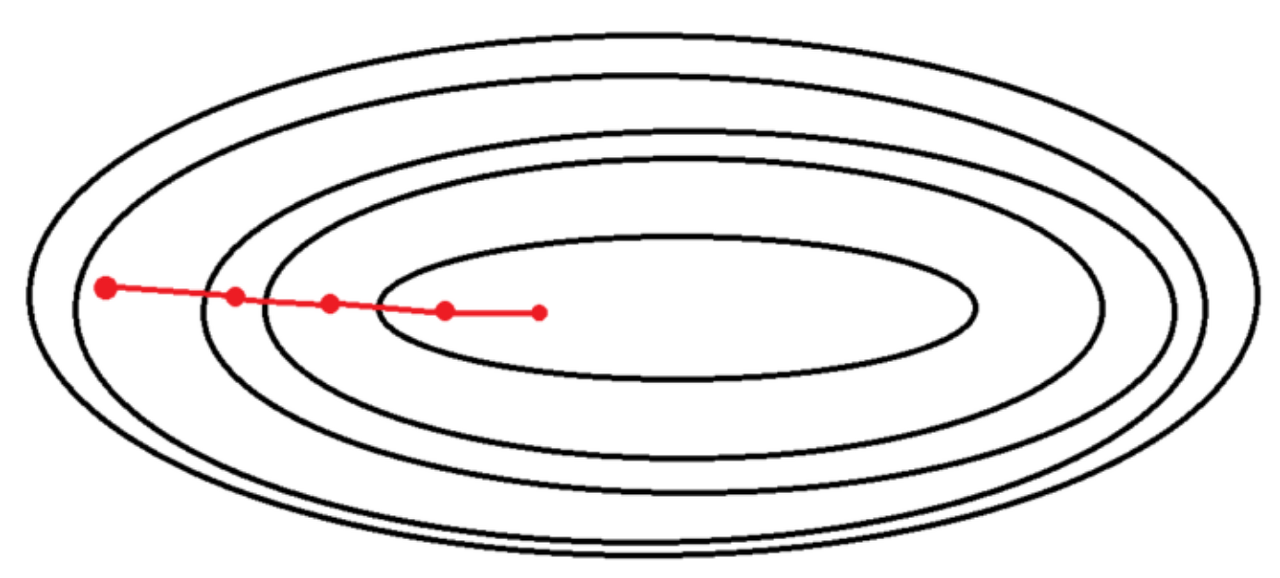
배치 경사 하강법(BGD)

출처 : https://wooono.tistory.com/93 $W_{t+1} = W_t - lr * g_t$
수식 변수 정리
- $W_t$ : Weight(가중치). 학습 해야 할 대상
- lr : 학습율
- $g_t$ : Gradient Vector

경사 하강법의 원리 모든 Data에 대하여 각각의 Gradient를 계산하고, 그들의 기댓값을 오차로 하는 것이다.
이렇게 구한 오차를 수식에 대입하여 Weight를 Update시켜 Loss를 최소로 하는 알고리즘이다.

장점으로는 Train Data를 모두 활용하므로, 수렴이 안정적이라는 점이다. 즉, Gradient의 방향 변환이 크지 않다는 것이다.

단점으로는 Local Optima(Local Minmum) Problem을 뽑을 수 있다.
Local Optima는 Global Minimum을 찾는 알고리즘에서 Global Minimum을 찾기 전 Local Minimum에 빠져 Local Minimum을 Global Minimum으로 인식하는 문제로써, 초기 W에 따라 Local Minimum에 빠질 수도 있고, Global Minimum을 찾을 수도 있게 된다.
신경망 Layer를 깊게 쌓았을 때 모든 층에서 Local Minimum에 빠질 확률은 매우 적기 때문에, 이러한 방법으로 Local Opitma 문제를 해결할 수도 있고, 이런 관점에서 사실 Local Optima는 없다라고 주장하는 사람도 있다.
두 번째 단점은 연산 Cost이다.
BGD는 모든 Data에 대하여 각각의 Loss Function을 계산하기 때문에, 연산 수가 Data에 비례하게 된다.
DL의 특징 상 데이터가 매우 많으므로, 연산 Cost도 매우 커지게 된다.

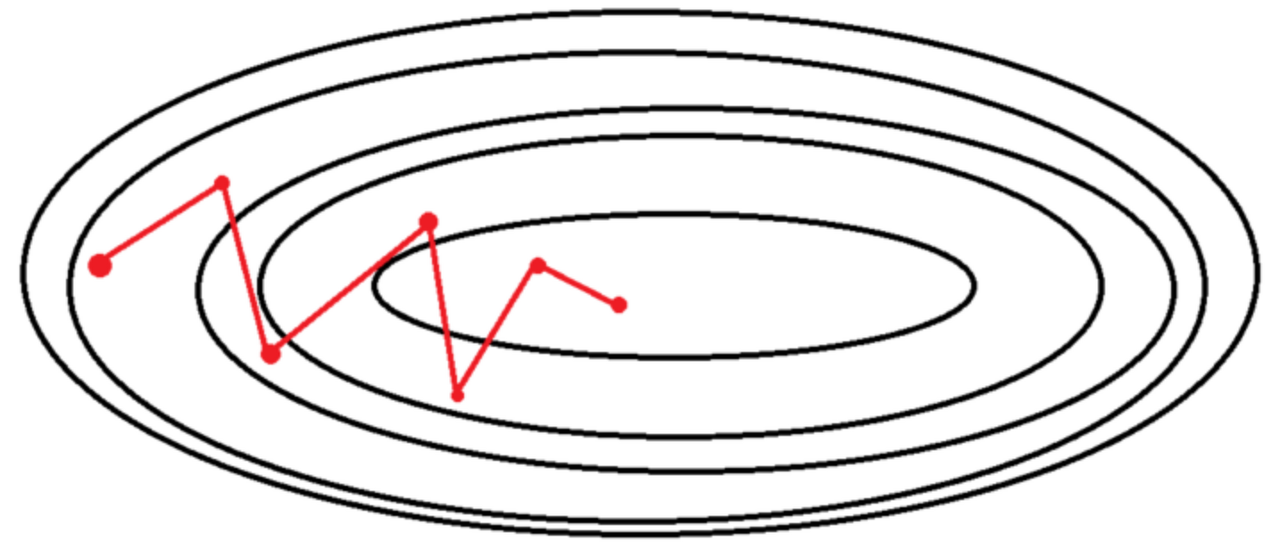
확률적 경사 하강법(SGD)

출처 : https://wooono.tistory.com/93 $W_{t+1} = W_t - lr * g_t$
경사 하강법과 수식 자체는 동일

SGD의 Batch는 전체 데이터 셋과 동일하다.(Batch Size = 1)
이러한 Batch에서 랜덤하게 한 개의 데이터를 뽑은 이후, Gradient를 구하여 경사 하강법을 활용한다

즉, 전체 데이터 셋(Batch)에서 1개의 랜덤 데이터를 뽑아 Gradient를 계산하고, 이렇게 구한 Gradient를 수식에 활용하여 Weight를 Update시키는 것이다

SGD의 장점은 Local Minimum에서 쉽게 빠져 나올 수 있고, Global Minimum을 찾을 가능성이 BGD보다 높다는 것이다.

SGD의 단점은 최적해(Global Minimum)에 정확히 도달하지 못할 가능성이 존재한다는 것이 크다.
2번째 단점은 "Shooting"이 있다.
"Shooting"이란 Gradient(기울기) 방향이 매번 크게 바뀌는 것을 말하는데, Data 개수와 상관 없이 1개 Data만 활용하여 Gradient를 계산하므로, Iteration이 매우 커지고 수렴 방향 차이가 커진다는 단점이 존재한다.

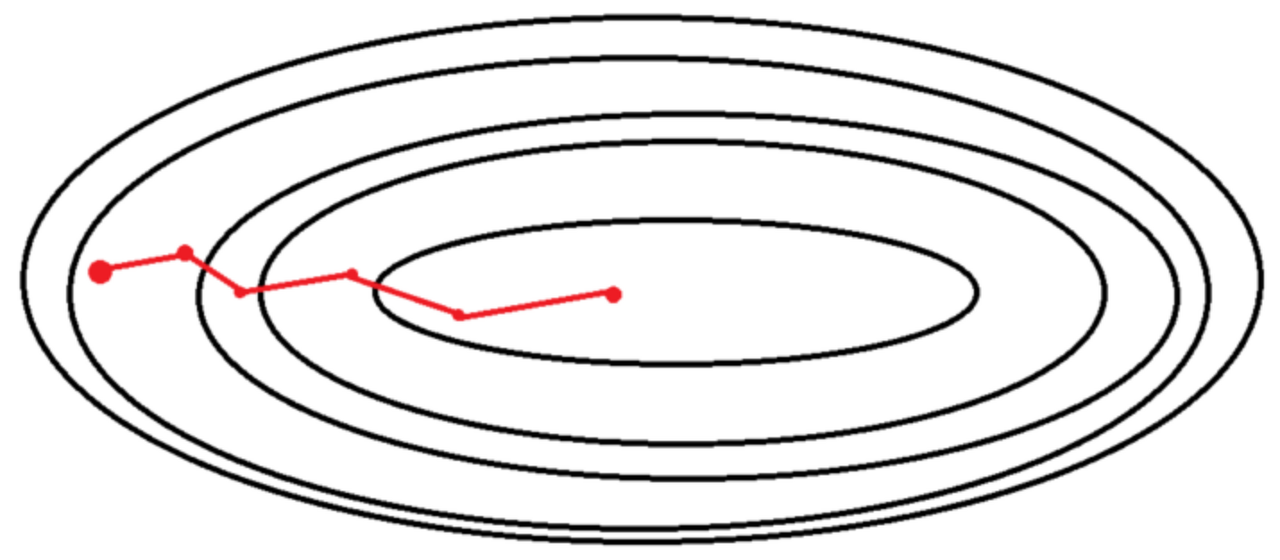
미니 배치 확률적 경사 하강법(MSGD)

출처 : https://wooono.tistory.com/93 $W_{t+1} = W_t - lr * g_t$
경사 하강법과 수식 자체는 동일

MSGD는 SGD에서 Shooting이 너무 많이 발생하는 것을 줄여, Shooting이 적당하게 발생하도록 해주는 알고리즘으로, BGD와 SGD의 절충안인 알고리즘이다.
참고로, 최근 SGD라고 하면 위에서 설명한 SGD보다는 MSGD를 통칭하는 경우가 더 많음

MSGD는 전체 데이터 셋을 Batch라는 여러 개의 Data Set Group으로 나눈다.(이 때 만들어진 Batch 개수를 Batch Size라고 한다)
이후, Batch 1개당 1번의 SGD를 수행한다. 즉, Batch 개수만큼 SGD가 수행될 것이고, 이 과정이 1 Epoch마다 수행될 것이다

이렇게 얻은 SGD 값들의 기댓값을 Gradient Vector로 정하고, 이 값을 활용하여 경사 하강법을 진행한다. 이렇게 Weight를 Update하면 다시 Batch마다 SGD를 수행하여 위 과정을 반복한다

MSGD의 장점으로는 Batch Size가 클 경우, BGD보다 속도가 빠르며, 메모리를 적게 먹는다는 것이 있다. 또한 Shooting이 적당히 발생하며, Local Optima 문제를 어느정도 회피할 수 있다는 장점도 가지고 있다.

MSGD의 Batch Size를 정할 때 고려할 점이 몇 개 존재한다.

Batch Size는 $2^n$ 승의 Size로 정하는 것이 좋음
강제는 아니지만, 대부분의 시중에 나온 메모리들의 Size는 $2^n$ 이며, 메모리를 최대한 활용하기 위해 이런 방법을 활용한다.
메모리 크기를 고려해야 함
메모리가 작은데 Batch Size가 너무 크면 OOM이 발생할 위험성이 존재한다.
전체 DataSet 개수가 2000보다 작다면 BGD가 빠름
만약 전체 데이터수가 Batch 개수에 나눠 떨어지지 않을 경우, 마지막 배치는 버리는 게 좋음

마지막 Batch는 버리는 게 좋은 이유

예를 들어 10000개의 Data가 존재하고, Batch Size가 100개라면 100개의 Batch 모두 총 100개의 Data를 가지고 있기 때문에 그대로 활용해도 된다.

하지만 10001개의 Data가 존재하고 Batch size가 100개라면, 100개의 Batch는 100개 Data를 가지고 있지만, 마지막으로 만들어지는 Batch는 1개의 Data만 가진다.

이런 경우, 마지막 Batch의 Data가 학습에 더 큰 비중을 갖게 되어, 마지막 Batch에 포함된 Data가 학습에 과도하게 큰 영향력을 끼칠 수 있다.

1개의 Batch마다 1의 가중치를 가지고, 이 1들을 종합하여 학습을 진행하는 것이다. Data를 뽑는 확률은 모두 같으므로, 100개의 Data를 가진 Batch는 1개 Data당 0.01의 가중치를 갖는다고 볼 수 있다.
그런데, 마지막 Batch는 1개 Data만 존재하므로, 해당 Data 자체가 1의 가중치를 가지게 된다.
즉, 마지막 Batch에 포함된 Data의 가중치(즉, 영향력)이 다른 Data에 비해 너무 커지기 때문에, 이런 과도한 영향력을 줄여야 할 필요가 있다

따라서, 모든 Batch의 Data 개수를 맞춰주기 위해 마지막 배치를 버리는 것이다

Batch Size에 따른 일반화 성능

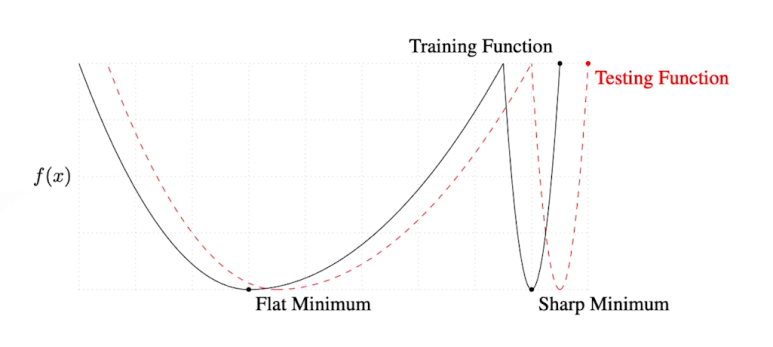
Batch size가 클 경우 Sharp Minimizer로 수렴하지만, Batch Size가 작을 경우 Flat Minimizer로 수렴한다.
Flat Minimizer는 왼쪽 그래프에서 수렴성을 찾는 것, Sharp Minimizer는 오른쪽 그래프에서 수렴성을 찾는 것이라고 알고 있으면 된다.

출처 : On Large-batch Training for Deep Learning Generalization Gap and Sharp Minima, 2017

일반화를 위해서는 Batch Size를 작게하여 Flat Minimizer를 갖도록 하는 것을 추천한다.

Flat Minimum 같은 경우 Testing Function과 Model이 차이가 조금 있더라도 Loss 값의 차이가 그렇게 커지진 않는다.
하지만, Sharp Minimum 같은 경우 차이가 조금이더라도 Loss 값의 차이는
너무 커지기 때문에 오차가 커진다.(그래프 참조)

즉, Generalizataion을 좋게 하기 위해 Flat Minimum을 추천한다.

앞에서 성능을 위해서는 Batch Size를 최대한 크게 하는 것이 좋다고 하였다. 하지만 Batch Size가 너무 크면 일반화 성능이 떨어질 수 있기 때문에 이 2개 요소를 고려하여 적절한 Batch Size를 고르는 것도 모델의 성능을 높이는데 중요한 요소라고 할 수 있다.