RNN

Sequence Data

소리, 문자열, 주가 등 시간 순서에 따라 나열된 Data로써, 과거의 사용 단어나 추세 등의 영향을 받는 Data를 의미한다.
주가, 문자열, 소리(대화) 등의 데이터가 존재한다.

과거 정보 또는 앞뒤 맥락 없이 미래를 예측하거나 결과물을 도출할 수 없는 Data로써, 독립동등분포(i.i.d) 가정을 잘 위배한다는 특징을 가진다.

i.i.d란 확률변수 $X_1, X_2, ..., X_n$이 상호 독립적이고 동일한 확률 분포를 가진다는 가정인데, Sequence Data는 과거에 영향을 받기 때문에 i.i.d 가정을 잘 위배하게 되는 것이다.
특히, 순서를 바꾸거나 과거 정보에 손실이 발생할 경우 데이터 분포가 바뀌므로, i.i.d 가정을 더 잘 위배하게 된다.

Sequence Data의 처리 Model

• Bayes' Theorem을 활용한 기본 Model

  $P\left({X}_1,{X}_2,...,{X}_t\right)\ =\ \prod _{s=1}^tP\left({X}_s\ |\ {X}_{s-1},...,{X}_1\ \right)$
  • 판단하는 시점보다 과거에 존재하는 모든 정보를 활용하여 현재 추세를 판단하는 방법

• 자기 회귀 모델

  • $X_1 \sim X_{n-1}$까지의 Data를 활용하지 않고 현재를 예측하는 모델
    • 과거 모든 Data를 활용하기에는 시간이 지날 수록 Model이 처리해야 하는 Data개수가 너무 많아짐
  • 판단을 위해 사용하는 길이가 $\tau$로 정해져 있을 경우, 이를 자기 회귀 모델이라고 함
    ${X}_{t+1}\ \ =\ P\left({X}_{t+1}\ |\ {X}_t,..,{X}_n \right)$
  • 고정된 길이($\tau$)를 어느 정도로 해야할지 항상 신경써야 함
    • 어느 때는 짧은 과거 Data로만 현재 상황을 추측할 수 있지만, 반대로 매우 오래된 Data가 필요한 경우도 존재
    • 고정된 길이를 결정하기 위해 외부 요인을 고려해야 하는 경우도 존재

• 잠재 AR 모델

  • 잠재 회귀 모델의 $\tau$ 모호성을 해결하기 위해 나온 모델
  • 잠재 변수로 과거 일정 길이 Data를 인코딩해서 활용하는 Model
    ${X}_{t}\ \ =\ P\left({X}_{t}\ |\ {H}_t \right)$
    $<{H}_{t} : X_1 \sim X_{t-1}\;\; Data를 \;\;Encoding한\;\; 잠재변수>$
  • RNN(순환 신경망)
    • 잠재변수를 인코딩하는 방법
    • 잠재변수 $H_t$를 신경망을 통해 반복 사용하여 Sequence Data의 패턴을 학습하는 모델

RNN의 순전파

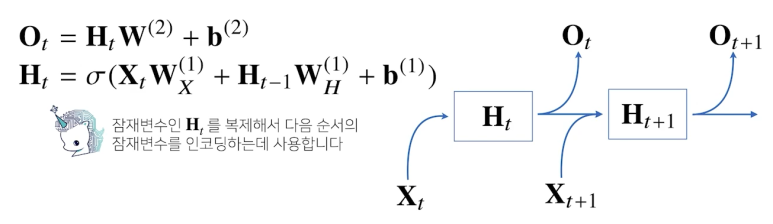
• $H_{t+1}$을 계산할 때 $H_t$(이전 잠재변수), $X_{t+1}$(입력 Data), b(절편 벡터)를 활용하여 계산
  • 이전까지의 Data를 활용하여 현재 Data를 파악
• W 행렬은 t가 변한다고 해도 절대로 바뀌지 않는 가중치 행렬

RNN의 역전파

BPTT(Backpopagation Through Time)이라고 하며, 순전파 과정에서 방향을 바꾸면 BPTT의 흐름이 된다.

• Loss Function에 대한 편미분(중간 계산 과정 생략)
  $\partial {w}_hh_t\ =\ \partial {w}_hf\left({x}_t,h_{t-1},w_h\ \right)\ \newline \quad \quad +\ \sum _{i=1}^{t-1}{\left(\textcolor{#ff0010}{\prod _{j\ =\ i+1}^t\partial {h}_{j-1}f\left({x}_j,h_{j-1},w_h\ \right)}\right)}\partial {w}_hf\left({x}_i,h_{i-1},w_h\ \right)$

위 수식에서 우리는 Sequence 길이가 길어질 수록 역전파의 학습 결과가 불안정해지기 쉽다는 것을 알 수 있다.

수식의 빨간색 부분이 Sequence 길이가 길어질 때 역전파를 불안정하게 하는 요인이다.
시퀀스 길이가 길어질 경우 Gradient의 계산이 매우 불안해진다.
예를 들어, 빨간 수식 값이 모두 2라고 가정하자. Sequence 길이가 1이고, 값이 하나 추가될 경우 1 -> 2로 Gradient가 변경되지만 변화값은 1밖에 되지 않으므로 안정감을 가진다.

하지만, Sequence 길이가 10으로 길어질 경우, 곱 연산은 1024의 값을 가지며 값이 하나 더 추가될 경우 1024 -> 2048로 Gradient값이 변경된다.
즉, 변화값이 매우 커 안정감을 가지지 못하고 계산이 불안해지는 것이다.

또한 기울기 소실 문제(Gradient Vanishing) 문제도 발생할 수 있다.
괄호의 값이 1/2이고 길이가 매우 길어지게 된다면 해당 값은 곱 연산이기 때문에 0에 빠르게 수렴할 것이다.
즉, 길이가 조금만 길어지더라도 과거 Data를 거의 활용하지 못하는
문제가 발생하게 된다.

이런 문제점을 해결하기 위하여 Sequence 길이를 끊어 BPTT를 수행하기도 하는데, 몇 개 Block을 형성하여 각각의 Block에 대해서만 역전파를 수행하는 것이다.

또한, 문제를 해결하기 위해 LSTM이나 GRU 같은 새로운 네트워크가 만들어지기도 하였다.

---

Sequential Model

Sequential Model이란

Sequential Data를 처리하는 여러가지 Model로써, Sequential Data는 과거 Data에도 의미가 존재하므로 Sequential Model은 과거 Data를 현재 예측값에 반영해야 한다는 특징을 가진다.

Sequential Data는 2가지 이유로 다루기가 매우 어렵다.
1. Sequential Data는 Input 길이를 특정할 수 없음

• Input Size가 매번 다르기 때문에 입력 Size와 Independent한 Model을 만들어야 한다는 이유

2. 데이터가 순서에 영향을 많이 받으므로 손실이 발생하거나 순서가 바뀌는 것에 대한 영향이 큼

• trimmed Sequence : 처음 Data나 마지막 Data 몇 개가 손실
• Ommitted Sequence : 중간 Data가 손실
• Permuted Sequence : Data 순서가 바뀜

Sequential Model 종류

• Naive Sequence Model : 이전에 들어온 모든 데이터를 활용하여 다음 Data 예측
  
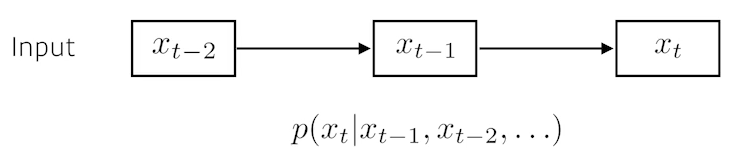
• AutoRegressive Model : 현재 데이터 값을 예측할 때 참조활 과거 데이터 개수를 한정하는 Model
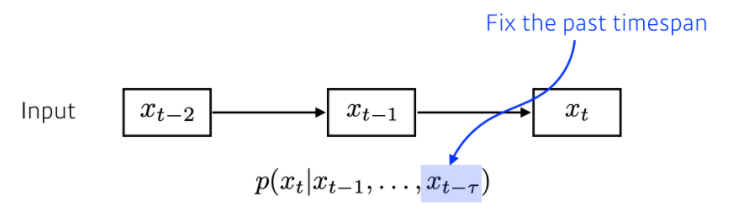
  • Fix the Past timespan
    
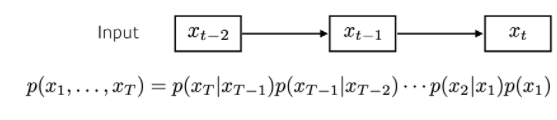
• Markov Model : 현재 Data는 직전 과거 Data 1개에만 Dependent한 Model
  • 다른 모델과 비교해봤을 때 과거의 정보를 많이 버려야 함
  • Joint Distribution(결합 분포)를 표현하기 쉽다는 장점을 가짐
    
• Latent AutoRegressive Model : Input과 Output 사이에 Hidden State를 생성하는 Model
  • Hidden State : Input과 직전의 Hidden State를 활용하여 도출됨
  • Hidden State는 과거으 ㅣ정보를 포함하고 있음
    

---

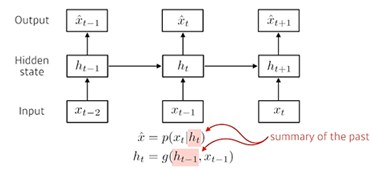
Vanilla RNN

Vanilla RNN이란?

기본적인 순환 신경망(Visual Recurrent Network)으로, Shallow NN 구조에 순환(Recurrent)를 추가한 Model이다.

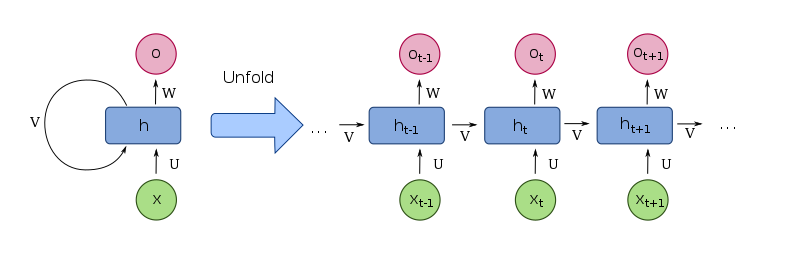
h 구간에서 Recurrent 과정인 v가 수행됨을 알 수 있다.

RNN 구조

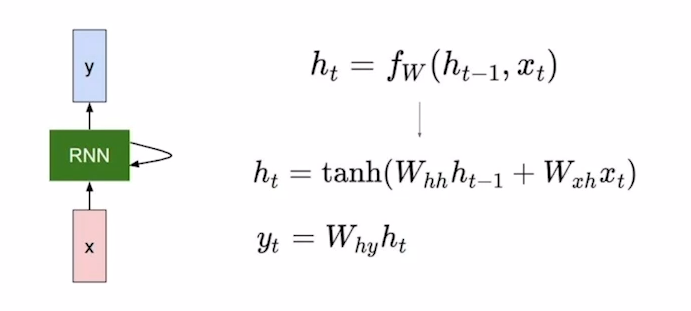
• $f_w$ 및 $W_{hh}, W_{xh}$는 모든 Time Step에서 동일함
• $h_{t-1}$ : Old Hidden-State vector
• x_t : Input Vector
• $h_t$ : New Hidden-State Vector
• $f_w$ : RNN Function with parameters W
• $y_t$ : Output Vector at time step t

같은 Function & 같은 Parameter가 모든 Time Step에 동일하게 적용한다는 특징을 가지며, 가장 처음 RNN이 시작할 때, 초기 Hidden State값($h_0$)는 0으로 초기화하여 빈 Vector를 전달해준다.

$W_{hh}h_{t-1} + W_{xh}x_t$에 대한 추가 설명

• 가정 : Hidden Vector의 Dimension은 2, x Vector(Input)의 Dimension은 3
  

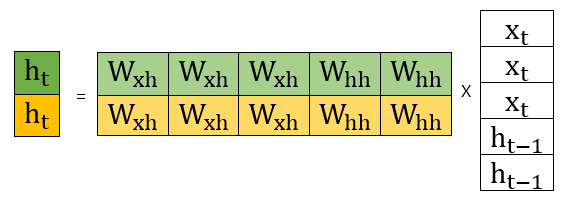
우리는 왼쪽 Matrix $h_t$를 구하고 싶은 것이다. 그리고, 이 연산을 위해서는 $W_{hh}h_{t-1} + W_{xh}x_t$를 수행해야 한다고 했다. 그렇다면 Matrix 2개를 형성하여 학습을 진행해야할까?
그것은 아니다. 이는 Matrix의 연산과정과 연관하여 이해하면 편하다
먼저 $x_t, h_{t-1}$ Vector를 Concat 시킨다. 위 예시에서 3,2로 각각 Dimension을 설정해줬으므로, Concat의 결과 5의 Dimension으로 설정될 것이다.(가장 오른쪽에 존재하는 Matrix)
이후 중간에 존재하는 Matrix인 2 X 5 꼴의 W(가중치 행렬)을 곱해주면 우리가 원하는 현재 Time Step의 Hidden State Vector를 구할 수 있을 것이다.
이 때, 행렬곱 과정을 생각하면 $W_{xh}$는 $x_t$와만 곱해지고, $W_{hh}$는 $h_{t-1}$와만 곱해지는 것을 알 수 있다. 단지, 초록색 부분은 초록색 부분의 연산값을 더해주고, 노란색 부분은 노란색 부분의 연산값을 더해주어 각각 초록색 $h_t$와 노란색 $h_t$를 형성함을 알 수 있다.
이는 결론적으로 한 개의 가중치 행렬 W를 2개로 쪼개 연산을 각각 수행한 이후 더한 값과 결과가 같을 것이다
($W_{xh}, W_{hh}$ Matrix로만 쪼갠 이후, $(W_{xh} * x_t) + (W_{hh} * h_{t-1})$의 결과와 같을 것이다)

RNN Type

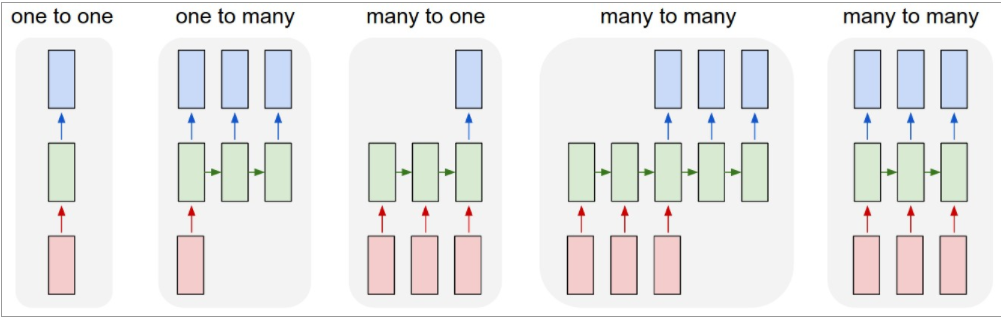
• One-to-One
  • Standard Neural Networks
• One-to-Many
  • Image Captioning
  • 이미지 하나를 주고, 이미지에 대한 설명글을 예측 혹은 생성하기 위해 Time Step 별로 여러 출력값을 내는 것
  • 첫번째 RNN에만 데이터를 넣어주고, 이후 Image와 같은 Size를 가지지만 값은 0으로 채워진 빈 Data를 RNN Model에 전달해 줌
• Many-to-One
  • Sentiment Classification
  • 문장을 단어로 쪼개서 RNN Time step 별로 단어 1개씩을 Input으로 넣어주고, 이렇게 해서 얻은 "최종적인" Output에 대해서만 Output Layer를 적용해 내가 원하는 값을 반환
• Many-to-Many(Delay)
  • Input이 모두 주어진 이후, Input에 해당하는 Output을 도출하는 형태
  • Machine Translation
• Many-to-Many(Undelayed)
  • 입력을 모두 받은 이후부터 Output을 받는 것이 아닌, Input에 대한 처리를 바로 하여 Output으로 반환해주는 형태
  • POS Stagging, Video classification on frame level
  • Character-Level Language Model
    • 학습을 끝낸 이후, Inference 때는 Model의 예측치를 다음 Time Step의 Input Data로 활용하여 예측 수행

BPTT

RNN에서 계산되는 Back Propagation로써, RNN에서는 Time도 매우 중요한 개념이므로, 이를 활용하여 Back Propagaation을 수행하는 것을 의미한다.

time step이 T일 때, T에서 Back Propagation 과정을 통해 얻어진 Data 뿐만이 아닌, T 이전에 발생한 모든 Back Propagation 결과값들을 활용하여 학습을 진행한다.

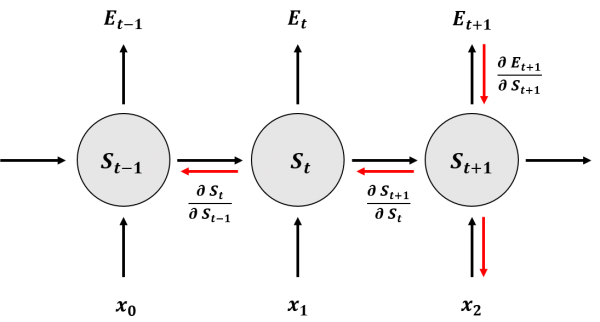
먼저 현재 시점(T)에서 Input과 Output을 활용하여 Error를 계산한다.
이후, Weight를 학습시킨다.

원래 BP라면 여기서 끝내고 다음 학습을 진행하지만 BPTT는 이렇게 학습된 Weight를 이전 RNN Model에 전파시킨다. 이전 RNN이라고는 하지만, 사실 RNN은 모두 같은 Weight를 활용하므로 Input과 Hidden State Vector 값만 바뀐 것이라고 할 수도 있다.
이렇게 전파된 Weight에 대하여 (T-1) 시점에서 다시 학습을 진행한다.
이 과정을 T번 거쳐, 첫 Input 시점($x_0$)에서 수행되는 RNN Model까지 Error를 전파시켜 학습을 진행시키는 것을 의미한다.

BPTT의 단점으로는 시계열 데이터의 시간 크기가 커지면 소비하는 컴퓨팅 자원이 증가한다는 것, 시간 크기가 커지면 역전파 시 기울기(Gradient)가 불안정해진다는 점이 있을 것이다.

BPTT 때 Hidden State Vector의 특정 Dimension 값을 고정시켜 변화를 확인할 수 있는데, 이 과정을 통해 해당 Dimension이 RNN의 순전파 과정이 수행될 때 어떤 역할을 담당하고 있는지 알 수 있다.

Truncated-BPTT

BPTT의 단점을 해결하기 위해 도입된 방식으로, 큰 시계열 데이터를 취급할 때 신경망 연결을 적당한 길이로 끊어 역전파를 수행하는 것이다.

T 크기를 전체 시간으로 설정하는 것이 아닌, 적당한 크기로 끊어 각각의 구간에서만 학습이 진행되도록 하는 것이다.

예를 들어보자.
Truncation 길이를 10으로 설정했다면, 1 ~ 10의 RNN 과정에서 BPTT를 수행하고, 11부터는 새로운 학습이 시작되는 것으로 생각한다. 즉, 원래라면 Time Step 20일 때의 BPTT는 20 -> 1까지 Error를 전파시켜 학습을 진행하였을 것이다. 하지만, Truncation 길이를 10으로 설정했으므로 20 -> 11까지만 Error를 전파시키고, 1 ~ 10까지의 Error에 대한 학습은 이미 진행되어 있는 것이다.

Vanilla RNN 단점

Long-Term Dependencies인 Data의 처리가 어려움

Sequence Data 중 관련된 요소(현재 Data 예측에 영향을 많이 줘야하는 요소)가
(시간적으로) 멀리 떨어져 있는 경우, Sequence에
Long-term Dependency(장기 의존성)이 존재한다고 한다.

Vanilla RNN 같은 경우 과거의 데이터를 h(Hidden State)를 통해 전달하는데,
step을 거칠 때마다 과거 정보가 지수적(Exponentially)으로 감소한다.

RNN에서는 가중치(Weight)가 0.5일 경우, step이 10번만 지나도
1/1024의 값을 가지기 때문에 현재 데이터에 영향을 끼치기 매우 힘들다.

Vanishing Gradient/Exploding Gradient

Vanilla RNN의 매우 큰 단점으로, 모든 Time Step에서 항상 동일한 W를 곱해주기 때문에, W가 1보다 작을 경우 Vanishing Gradient가, W가 1보다 클 경우 Exploding Gradient가 발생함

학습 과정에서(Backpropgataion 과정에서) Gradient가 기하급수적으로 작아져서, Optimal Solution을 구하는 데 도움을 줄 수 없는 Vanishing Gradient 현상이 발생할 가능성이 존재한다.

반대로, 학습 과정에서 Gradient가 기하급수적으로 커져 NaN 값을 가지고, 학습을 진행할 수 없는 상태가 되는 Exploding Gradient 상황이 발생하기도 한다.

특히 ReLU 함수는 Exploding Gradient를 발생시킬 가능성이 높은 활성함수이므로, RNN에서는 잘 활용하지 않는다.

물론 CNN 등 다른 알고리즘에서도 많이 발생하는 문제점이지만, RNN은 특히 같은 가중치를 가진 계산(h)이 반복되고, Size가 큰 Data가 들어오는 경우가 많아 이런 문제점이 더욱 부각된다.

이런 장기 의존성과 Gradient에 관련된 단점을 해결하기 위하여 LSTM, GRU 개념이 도입되었다.