LSTM
LSTM이란
2개의 State를 가지는 Model로써, Hidden State + Cell State를 가진다.
Vanilla Rnn은 하나의 Hidden State만 가지는 것과 비교하여 가장 큰 특징이다.
Input Gate, Forget Gate, Output Gate라고 불리는 3개의 Gate 구조가 추가되었다.
추가된 Gate를 활영하여, 과거의 Data 중 버릴 것을 결정하여 버리고 필요한 Data는 유지시켜 Long term Dependency를 가진 Data에 대해서도 잘 처리하게 만들었다.
과거 Data 손실을 적게 하고, 필요 없는 Data는 버려 Size를 작게 했다.
이전 Time Step의 Hidden State Vector 중 필요한 정보를 "덧셈"을 활용하여 다음에 수행되어야 할 Model의 Input 정보를 만든다는 특징을 가지고, 이는 Vanishing Gradient나 Exploding Gradient 문제가 잘 발생하지 않는다는 장점을 가지고 왔다.
LSTM 구조
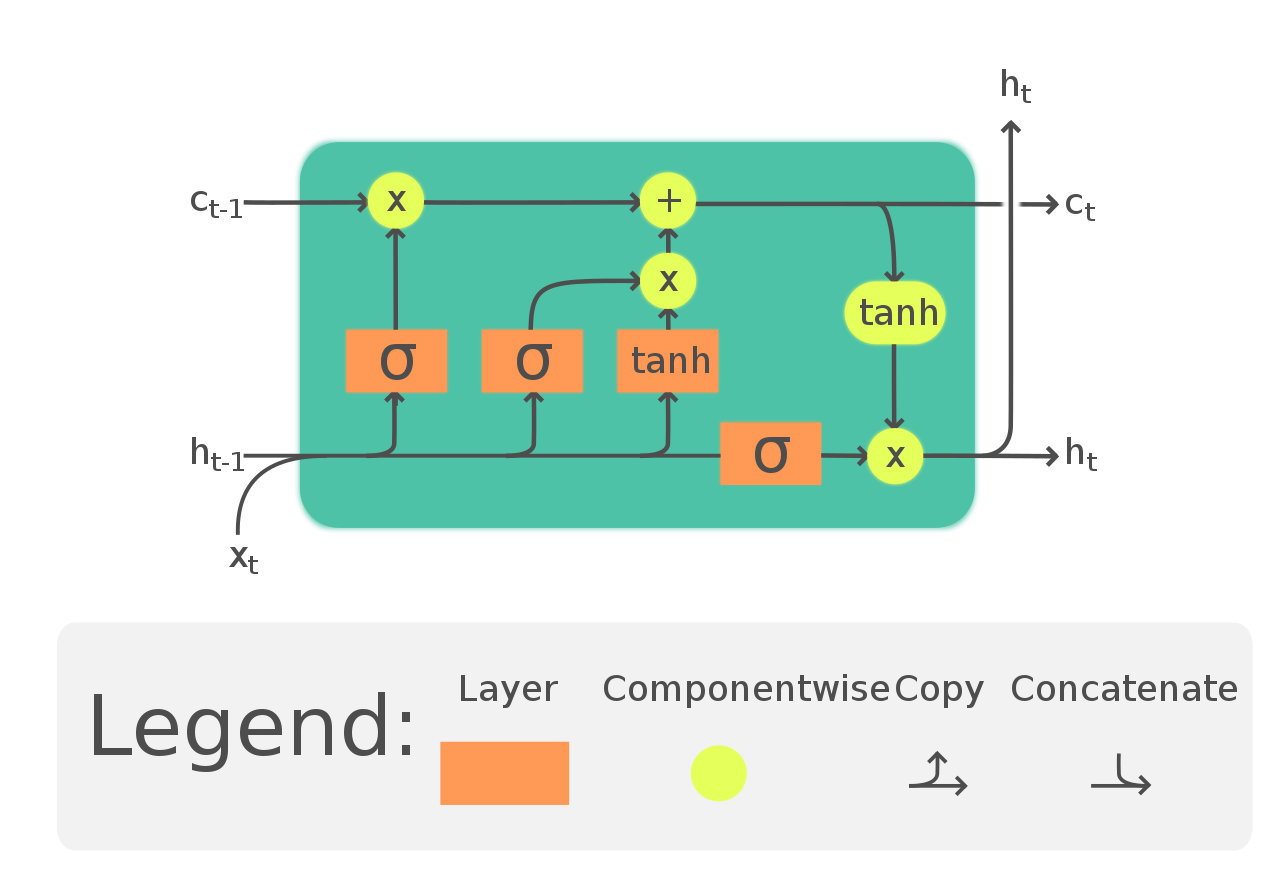
- 출처 : https://en.wikipedia.org/wiki/Long_short-term_memory#/media/File:LSTM_Cell.svg
- LSTM 모듈의 기본적 구조
- : Cell State
- : Hiddne State(Output)
- : Input Data
- ρ : Sigmoid 활성 함수
- 0과 1 사이 값을 내보내고, 이는 과거 정보를 어느정도 보존해야 하는지에 대한 척도가 됨
- LSTM 2가지 State
- Cell State
- 이전까지의 정보를 Summarize하는 State
- Linear Interaction만 적용시키면서 계속해서 흘러감
- 절대로 모듈 밖으로는 도출되지 않는 값
- Hidden State(Output)
- 직전 모듈에서 반환한 Output
- Cell State
한 눈에 보는 LSTM
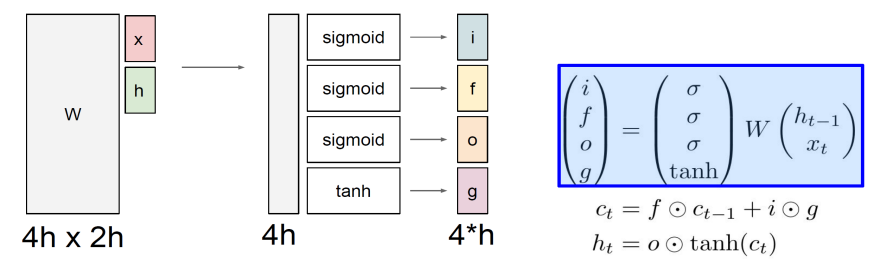
- x : Input Data, h : Hidden State Vector
W(가중치 행렬)에 x와 h를 Concat 시킨 Vector를 곱해주면 최종적으로 4h X 1 형태의 Matrix가 나올 것이다. 이 부분을 4등분하여 각각의 Part마다 특정 함수를 적용하면, LSTM에서 활용하는 각각의 Gate를 구할 수 있다.
Input Gate
i에 해당한다.
Cell에 이번 Input Data를 얼마나 적용할지 결정한다.
Gate gate
g에 해당한다.
Data 값을 얼마나 Cell에 적용시킬지를 결정한다.
Output Gate
o에 해당한다.
Cell State를 어느 정도 보존하여 Hidden State Vector를 만들지 결정해준다.
Forget Gate
f에 해당한다.
이전 Cell State를 어느 정도로 보존할지 정해준다.
- : Cell State 연산 과정.
이전 Cell State()을 어느 정도의 비율로 보존시키고(forget gate; ), 현재 Data(g; Gate gate)를 어느 정도 비율로(i; input gate)로 반영시킬지 결정한 이후 현재 Data를 "더하기" 연산을 통해 Cell State에 반영시켜줌 - : Hidden State 연산 과정
위에서 먼저 Cell State를 Update 시킨 이후 수행되는 연산. Cell State를 Update시키고, 이 Cell State를 어느 정도 비율(o; Output gate)로 보존시켜 최종적인 Hidden State Vector로 만들지 결정함
g(Gate gate)와 i(Input Gate)의 차이
처음 공부했을 때 가장 이해가 되지 않은 부분이였다.
용어가 겹쳐서 조금 어려운데, 쉽게 말하자면 는 우리가 최종적으로 LSTM 연산에 활용할 Cell State, 인 Gate gate는 오로지 이전 Hidden State Vector와 Input Vector만을 통해 구한, Vanilla RNN에서의 현재 시점(T)에서의 Hidden State Vector라고 생각하면 된다.
단지, LSTM의 Hidden State Vector는 최종적인 Cell State 를 활용해서 구하기 때문에, Vanilla RNN을 통해 구한 Hidden State Vector를 Hidden State Vector라고 말하면 의미가 다른데 용어가 겹치므로 활용할 수 없다. 따라서 Gate gate라는 별다른 용어를 활용하는 것이다.
Cell State는 과거 정보를 담는 State, Hidden State는 Cell State를 활용하여 도출한 Hidden State Vector라고 생각하면 된다.
Hidden State Vector가 Output으로 반환되고, 다음 LSTM Model에 전달된다.
Gate gate는 Vanilla RNN에서 과 를 활용해 얻을 수 있는 Hidden State Vector이다.
단지, LSTM에서는 이렇게 구한 Hidden State Vector를 Cell State에 적용시켜 최종적인 Cell State를 구하고, 이렇게 구한 최종적인 Cell State로 Hidden State Vector를 구하므로 용어의 분리를 위해 새롭게 만든 용어이다.
LSTM 동작 과정(단계별)
Step 1 : Forget Gate
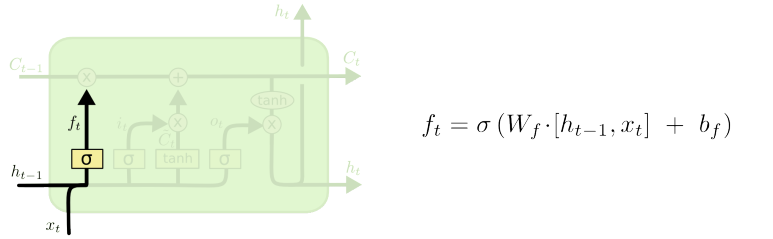
- (이전 Module의 Cell State) 중 지울 데이터와 유지할 데이터를 정하는 과정
- 과거 데이터 중 필요하지 않은 부분들을 삭제하고 남은 데이터들도 가중치를 적용하여 Data 유지하기 위한 함수 생성 과정
- 활성 함수(Sigmoid) 값이 0이라면 해당 Data는 지우고, 1이라면 해당 Data는 유지해서 다음 모듈에 전달해 주는 것
Step 2 : Input Gate
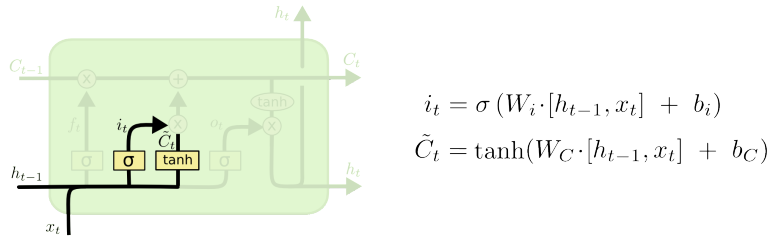
- 이전 Cell State에 저장할 Data를 결정하는 과정
- 이전 Module에서 전달받은 Cell State에 현재 데이터를 반영해야 이번 Module의 완벽한 Cell State가 됨
- Cell State에 현재 Input을 반영하는 과정
Step 3 : Update Cell
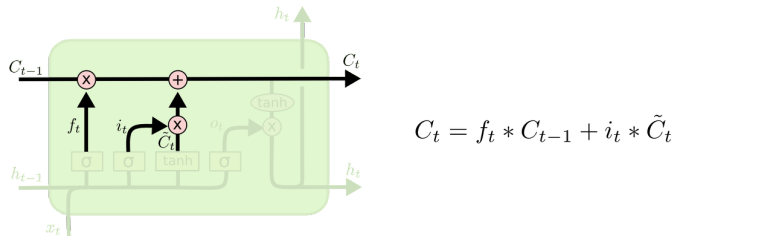
- Input Gate로 처리한 현재 데이터와 Forget Gate로 처리한 를 활용하여 Cell state를 Update
- 이전 Module에서 반환한 Cell State 중 필요하지 않은 Data를 삭제하고(x 연산), 현재 Data를 Cell State에 반영하는(+ 연산) 과정
- : (이전 Cell State를 반영하지 않고) 해당 Time Step t 때 만들어진 Gate gate와 이전 LSTM Model에서 전달된 Cell State에 이번 Input Data를 어느 정도로 반영할지 결정하는 를 곱해주어, 최종적으로 이번 Time Step에 만들어진 Cell State(Gate gate)를 어느 정도로 반영할지 결정해주는 연산
Step 4 : Output Gate
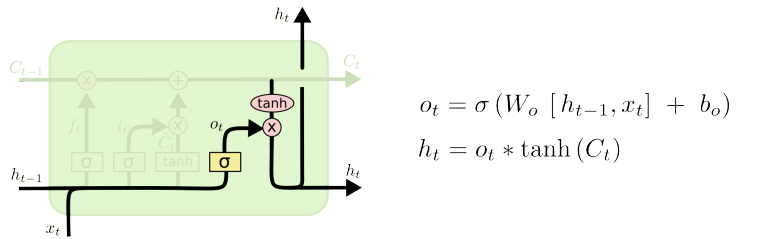
- Update Cell에서 구한 를 활용하여 Output(Hidden State)를 반환하고, 동시에 다음 Module에 Output을 전달함
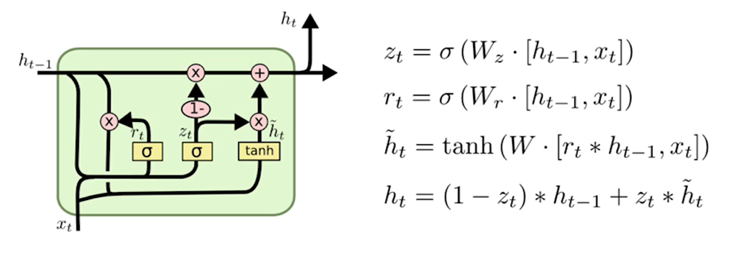
GRU(Gated Recurrent Unit)
LSTM에서 Cell State를 없애고 Hidden State만 활용한 Model로써, Reset Gate와 Update Gate만 존재한다.
를 활용하여 (Forget Gate)와 (Input Gate)를 동시에 대체했다.
Gate 수를 줄였기 때문에 계산 과정 및 State를 줄여 Paramter가 줄어든다.
계산양과 메모리 사용량을 줄인, LSTM이 경량화 된 모델이다.