Regularization

Regularization이란?

일반화 성능을 높이는 방법으로, Overittin을 방지하는 기법들을 말한다.
학습을 일부러 방해하는 것을 통해 일반화 성능을 높인다.

Early Stopping

Generalization Gap이 커질 때 학습을 멈추는 방식으로, 어떤 방식으로든 Train에 참여하지 않은 Data로 Test한 이후, Generalization Gap을 계산하여 Training 멈춘다.
(이 때 대부분 Cross Validation을 활용하여 멈추는 시점을 선택한다)

Parameter Norm Penalty

Parameter가 너무 커지지 않도록 하는 것이다.
Parameter가 너무 커지면 과하게 구불구불한 형태의 함수가 만들어지고, 이는 Overfitting의 원인이 된다

• $(||W||_2)^2$ : Parameter Norm Penalty

Total Cost를 미분하면 W 앞에 특정 값이 곱해진다. 이를 Weight Decay라고 한다.
Weight Decay에 의하여 가중치가 비 이상적으로 커지는 일을 방지하는데, Weight Decay에 큰 영향을 주는 값이 위 수식에서 'a'이고, 규제 강도라고도 부른다.

Weight Decay 값이 커지면 가중치 값이 작아지며, 자연스럽게 Overfitting 현상이 줄어든다.(가중치 값이 너무 커지면 Weight Decay에 의해 Penalty가 발생하여 너무 커지지 않음)
하지만, Weight Decay 값이 너무 크면 가중치 값이 Update가 잘 되지 않아 Underfitting이 발생할 수 있으므로, 적당한 값을 활용해야 한다.

Data Augmentation

Data가 많아질수록 DL의 성능이 좋아지므로, Data의 양을 늘릴 필요가 있다. 이를 위해 Data Augmentation(데이터 증강)을 수행한다.

Text에서는 Backtranslation, 이미지에서는 Data를 회전시키는 등의 방법을 활용하여 1개 데이터를 변형시켜 여러 개 Data가 있는 것처럼 Data 양을 늘리는 방법이다.
이 때, Data 종류에 따라 Data의 Label(Target)이 바뀌는 경우가 존재하므로 Data Augmentation 방법을 신중히 고를 필요가 있다.

Noise Roubustness

입력 Data 뿐만이 아닌 Weight에도 Noise를 적용하여 계산을 정확히 하는 방법이다.

Label Smoothing

학습 데이터 2개를 뽑아 데이터를 섞어주는 방식으로, Decision Boudnary를 부드럽게 만들어주는 효과를 가진다.

• Image에서 대표적인 Label Smoothing 방법
  • mixup : 이미지 2개를 고른 뒤, 두 데이터를 (Smooth하게) 섞음
  • cutout : 특정 데이터의 일부 영역을 잘라 데이터를 평가
  • cutmix : 이미지 2개를 고른 뒤 특정 Data 1개를 cut하여 (Smooth하지 않게) 다른 Data에 붙임

Dropout

Layer 개수가 많아졌을 때는 일반적으로 많은 문제를 해결할 수 있도록 학습 능력이 좋아진다는 장점을 가지고 있다.
하지만, Overfitting의 가능성이 높아지며, 신경망에 대한 학습 시간이 길어지고, 훈련 데이터 양이 많이 필요하다는 단점이 존재한다

특히, 훈련 데이터 양이 많이 필요하다는 것에 집중하자. 층이 깊을수록 좋으니 너무 많은 층을 만들어버리면, 데이터의 양에 비해 Layer가 깊어져 Overfitting의 가능성이 급증한다

Dropout은 학습을 진행할 때 일부 뉴런 값을 0으로 만들어, 학습 과정에서 해당 뉴런을 생략해 줄어든 신경망을 통하여 학습을 수행하는 것이다. 학습 과정에서 생략할 뉴런은 랜덤하게 선택된다.

장점으로는 Voting에 의한 평균 효과를 얻을 수 있어 Regularization과 비슷한 효과를 얻는다는 것이 있을 것이다.
또한 앙상블과 비슷한 효과를 내기 때문에 성능 향상을 가지고 온다는 장점도 가진다.

Co-adaption이라는 현상을 방지할 수 있다는 장점도 가지는데, Co-adpation이란 특정 뉴런의 Bias나 Variance가 커질 때, 해당 뉴런의 영향으로 학습이 느리게 진행되거나 다른 뉴런들이 영향을 받아 잘못된 방향으로 학습이 진행되는 것을 의미한다.

• 공부한 사이트 : https://m.blog.naver.com/PostView.naver?isHttpsRedirect=true&blogId=laonple&logNo=220542170499

Batch Noramlization

내가 적용하는 Layer의 statics를 정규화하는 것으로, Layer Parameter들의 평균과 표준편차를 구한 뒤, 정규화시켜 Parameter 크기를 줄이는 방식을 택한다.

정규화란, 평균을 빼고 표준편차를 나눠줘 값을 작게 하는 과정이다.

---

Batch Normalization

기존 Batch 단위 학습의 문제점 : Internal Covariant Shift

아래 사진을 보면, 학습 과정에서 계층 별로 입력의 데이터 분포가 달라지는 현상이 발생할 수 있다

• 사진 출처 : https://gaussian37.github.io/dl-concept-batchnorm/

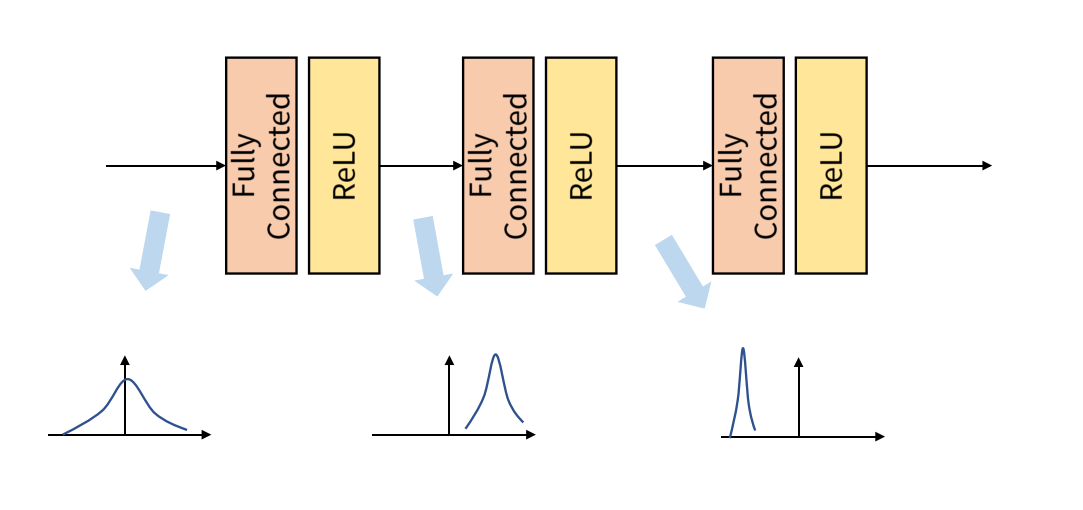
Model을 통과하기 전과 후 데이터 간 분포가 달라질 수 있는데, 만약 Batch 단위로 학습하면 Batch 단위간 데이터 분포의 차이가 발생할 수 있다.
(데이터마다 Model 통과 전후 분포가 달라질 것이므로)
이런 현상을 Internal Covariant Shift라고 하며, 모델 성능에 악영향을 미친다.

Batch Normalization 도입 이유

Internal Covariant Shift 문제를 해결하는 3가지 방법이 존재한다.
1. Change Aacitvation function : ReLU의 활용
2. Careful initialization : 가중치 초기화를 잘 함
3. Small Learning Rate : learning rate를 작게 설정함

하지만, 위 3가지 방법은 간접적인 방법의 해결 방법으로 궁극적인 문제는 해결하지 않는다.
이런 문제를 직접적으로 해결하는 것이 Batch Normalization이다.

또한 Batch Normalization을 활용하면 평균과 분산이 지속적으로 변하고 Weight Update에도 계속 영향을 주어 가중치가 큰 방향으로만 학습되지 않아 Overfittin을 방지하는 Regularization 효과를 낼 수 있다는 점도 도입된 이유이다.
(Overfitting 문제에 좀 더 Robustness)

마지막으로, Local Optimum에 빠질 수 있는 가능성을 낮춘다는 장점도 가지고 있다.

Batch Normalization

Internal Covariate Shift를 없애기 위해 Layer 및 Batch 별로 Batch Normalization Layer가 추가 되어 Normalization을 해주는 기능을 말한다.

• 사진 출처 : https://gaussian37.github.io/dl-concept-batchnorm/

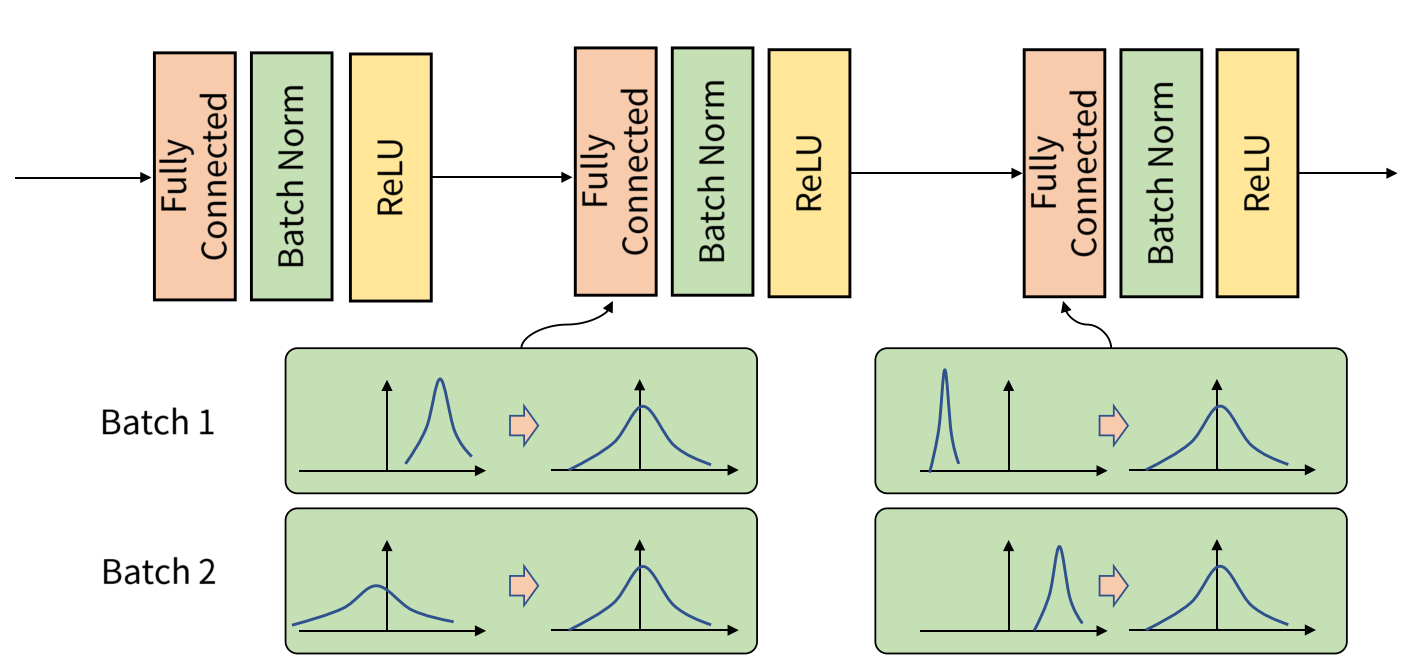
각 Batch별로 평균과 분산을 활용하여 정규화 하는 것으로, Batch 단위나 Layer에 따라 입력 값 분포가 모두 다르지만 정규화를 통해 Zero mean gaussian 형태로 만드는 과정이다.

학습 단계에서는 Normalization 이후 Activation Function에 대해 적합한 Scaling 및 Bias를 적용하기 위한 $\gamma, \beta$를 활용한다.

• $\gamma$ : 추가 Scaling
• $\beta$ : 편향

이 2개 요소는 Backpropagation을 통해 학습할 수 있는 값들로써, 모든 계층의 Feature가 동일한 Scale이 되어 lr 결정에 유리해지고, Scale 및 Bias도 학습하기 때문에 Activation에 적합한 분포로 변환 가능하게 된다.

추론 단계에서의 Batch Normalization은 학습 시와는 약간 다른 방식으로 진행된다. $\gamma, \beta$ 및 평균, 표준 편차 모든 값을 고정하여 Batch Normalization을 수행한다.

Batch Normalization 단점

• Batch 크기에 영향을 많이 받음
• Batch 크기가 너무 작음
  • 큰 수의 법칙, 중심 극한 이론을 만족하지 않으므로 데이터 전체 분포를 표준 편차가 잘 표현하지 못함
• Batch 크기가 너무 커짐
  • 병렬 연산에 있어 비효율적임
  • Batch 크기가 너무 크면 Multi Model 형태의 Gaussian Mixture 모델 형태가 나타날 수 있어 Batch Normalization이 좋은 Modeling이라고 말할 수 없음
  • Gradient 계산을 한번에 하게 되므로, 학습에 악영향을 끼칠 수 있음

이런 단점을 해결하기 위해 Weight Normalization, Layer Normalization 등을 활용하기도 한다.

Instance/Layer/Group Normalization

• Instance Normalization
  • 이미지 스타일 변환에 주로 활용됨
  • Mini-Batch의 이미지 한장씩만 계산하여 각각의 개별 이미지 분포를 활용
• Layer Normalization
  • Mini-batch Sampler간 의존 관계 없음
  • Channel에 전체 데이터에 대하여 Normalization 수행
  • Batch Norm의 Mini-Batch Size를 뉴런 개수로 변경
  • 작은 Mini-Batch를 가진 RNN에서 성과를 보임
• Group Normalization
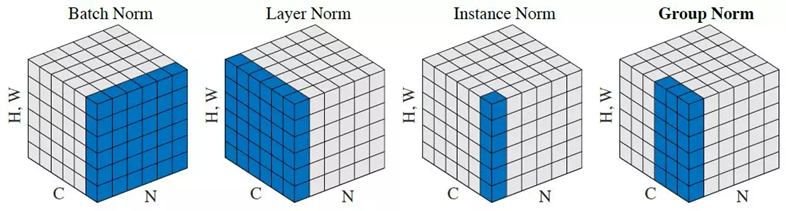
  • 각 Channel을 N개의 그룹으로 나누어 정규화