CNN

Convolution

Kernel을 입력 벡터 위에서 움직여 가며 선형 모델과 합성 함수가 적용되는 구조를 의미한다.
아래 사진을 보면 Filter를 Input Data 위에서 움직여가며 연산을 수행하는데, 이 연산을 Convolution이라고 말한다.

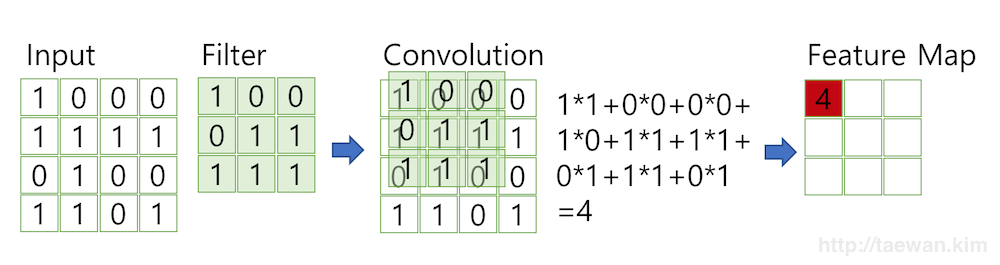
• 사진 출처 : http://taewan.kim/post/cnn/

• 수학적 의미의 Convolution

  • f, g가 Continuous
    $[f*g](x)\ =\ \int_{{R}^d} f\left(z\right)g\left(x-z\right)dz\ =\ \int _{{R}^d}f\left(x-z\right)g\left(z\right)dz\ =\ \left[g*f\right]\ \left(x\right)$
  • f, g가 Discrete
    $\left[f*g\right]\ \left(x\right)\ =\ \sum _{a\in {R}^d}^{ }f\left(a\right)g\left(i-a\right)\ =\ \sum _{a\in {R}^d}^{ }f\left(i-a\right)g\left(a\right)dz\ =\ \left[g*f\right]\ \left(x\right)$
  • 신호(Signal; f(x))를 커널(g(x))를 이용하여 국소적으로 증폭 또는 감소시켜 정보를 추출하거나 필터링 하는 것

Kernel은 계속해서 움직이지만 절대로 값이 변경되지는 않는, 말 그대로 Filter이다.
이런 커널을 국소적(Local)으로 적용하기 때문에, Transolation Invariant의 특징을 가진다.

CNN에서 translation invariance란 input의 위치가 달라져도 output이 동일한 값을 갖는것을 말하는데, 이미지에서 왼쪽 위에 고양이가 있든 오른쪽 아래에 고양이가 있단 두 데이터 모두 고양이를 표현한다는 의미를 가진다.

1차원 뿐만이 아닌 다양한 차원에서 계산이 가능하고, 단지 Channel이 여러개인 2차원 Data의 경우, 2차원 Convolution을 Channel 개수만큼 적용하기만하면 된다.

위 말을 풀어서 하면 2차원 Kernel을 N층으로 복사하고, 이를 3차원 입력에 대해
Convolution으로 수행해주면 되는 것이다.

예를 들어, Dimension이 각각 Kernel은 (A,B,C)이고 Data는 (H,W,C)라고 가정하자.
이 때, Convolution을 수행할 경우 Kernel에서 (a, b, x) 구간을 뽑았다면, Data에서도 (h, w, x) 구간을 뽑아 같은 x를 가진 Kernel과 Data 부분을 뽑아 연산을 수행해주는 것이다.
즉, Data와 Kernel에서 x 위치에 존재하는 것들만 뽑아 2차원 Convolution을 수행해주고, 모든 x에 대해 이런 연산을 수행한 이후 이렇게 나온 2차원 결과값들을 모두 더해주면 Channel이 여러 개인 Data의 Convolution도 수행할 수 있는 것이다.

이 말인 즉슨, C 숫자가 무엇이든 간에 결과값은 (O1, O2, 1)로 나온다는 것이다

• 만약, $(O_h, O_w, O_c)$로 Convolution 연산 결과값을 만들고 싶다면, Kernel를 총 $O_c$개 활용하여 Convolution을 수행해주면 된다

Convolution 연산의 역전파(Back Propagation)

• 수학적 의미의 Convolution 역전파 : $\frac{\partial }{\partial x}\left[f*g\right]\left(x\right)\ =\ \left[f*g'\right]\left(x\right)$

역전파를 알기 위해서는 먼저 순전파에 대한 이해가 선해되어야 한다.

CNN에서 커널을 통한 순전파 과정

CNN에서 input값이 들어올 경우, Model을 활용해 출력을 내는 과정으로, 입력 값에 대해 커널을 움직이며 곱 연산을 수행한다.

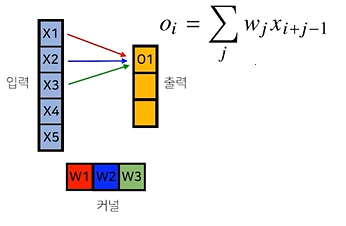
CNN에서 일어나는 역전파

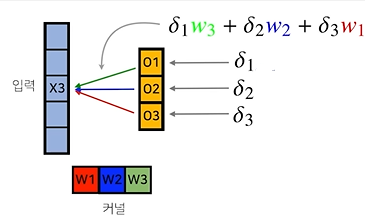
• $δ_1$ : Gradient 값

위 2개 사진을 보며 이해하는 것이 편하다.

1. 순전파 과정에서 $o_1$을 만들기 위해 $(w_3, x_3)$가 활용되었고, $o_2$는 $(w_2, x_3)$, $o_3$는 $(w_1, x_3)$가 활용되었음을 볼 수 있다.

2. 역전파는 순전파의 역방향으로 미분(Gradient) 값을 활용해 학습하는 것이다.

3. Input 기준으로 관점을 바꿔보자.

• $x_3$는 $w_3$와 함께 $o_1$을 만들었다. 즉, 역전파에서는 $w_3$dhk $o_1$에 관련된 Gradient인 $δ_1$이 같이 활용된다. 따라서, $δ_1 * w_3$ 연산이 수행된다.
• $w_2, w_1$일 때도 같이 생각해보면, $δ_2 * w_2$, $δ_3 * w_1$ 연산이 수행되어야 함을 알 수 있다.

4. Kenrel 기준으로 살펴보자.

• $w_1$같은 경우 $x_3$와 곱해져 $o_3$를 형성했다. 반대로 생각하자면, $w_1$의 Gradient에는 $δ_3 * x_3$ 요소가 포함되어야 할 것이다.($o_3$와 관련된 Gradient는 $δ_3$)
• $w_2$, $w_3$도 이와 같이 생각하자면, $δ_2 * w_3$, $δ_1 * w_3$ 요소가 포함되어야 함을 알 수 있다.

5. 마지막으로 $x_3$ 뿐만이 아닌 $x_1 ~ x_n$까지 모든 Input Data에 대해 연산을 적용시켜보자. 우리가 구하고 싶은 값은 $w_i$에 대한 미분을 활용하여 학습하는 것이므로, 아래와 같은 수식을 활용하여 역전파 알고리즘이 수행될 것이다.
   $\frac{\partial L}{\partial{w}_i}\ =\ \sum _j^{ }{\delta }_j{x}_{i+j-1}$
   • L : Loss Function

CNN Layer

Convolution Layer

입력된 이미지에서 테두리, 선, 색 등 이미지의 특징이나 특성을 감지하는 목적으로 만들어진 Layer이다.

입력 계층으로는 Kernel을 통해 처리해 줄 Data가 들어오고, 은닉 계층(Hidden Layer) : Kernel을 통해 입력 계층을 처리한 이후의 Data가 존재한다.

Kernel 이외에 1개의 편향 값(Bias)를 적용하여 Hidden Layer Data를 생성한다.

이 Layer에 Kernel은 이미지를 인식하기 위해 필요한 가중치를 줄이고, 이를 통해 연산량을 대폭 감소시키기 위해 활용한다.

Pooling Layer

Convolution Layer 이후 Data에서 특정 범위의 값들 중 하나를 선택해서 가지고 오기 위한 목적의 Layer이다.

Max Pooling, Average Pooling 등의 방법 존재하며, 영역 내 이미지나 영상 위치가 조금 변경되더라도 아무 지장 없이 인식할 수 있게 해준다는 장점을 가지고 있다.

Fully Connected Layer

처리된 Data들을 모두 연결시키고 1차원 배열로 풀어서 표시하는 목적을 가진 Layer로써, Decision Making(Classification)을 위해 활용된다.

해당 Layer는 입력과 출력을 모두 연결해주는 Layer인 Dense Layer로 생각할 수 있다.

Layer 관련 용어

Channel

Data가 쌓인 계층이다.
RGB로 이미지를 표현하면, R에 해당하는 Data, G에 해당하는 Data, B에 해당하는 Data가 존재하기 때문에 총 3개 Channel로 형성되어 있다.

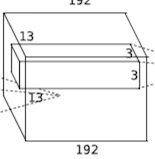
• 아래 사진을 보면 13 * 13의 Data가 192개 모여 우리가 원하는 Data 1개를 형성한다. 이 때, 192가 Channel을 의미한다
  

Convolution & Pooling Layers

CNN에서 Feature Extraction을 위해 활용하는 Layer로, 이미지에서 유용한 정보 뽑아오는 역할을 수행한다.

Fully Connected Layer

Fully Connected Layer를 줄이거나 사용하지 않는 것이 추세이다.
대신, Convolution 및 Pooling Layer를 많이 만들어 층을 깊게하는 추세이다. 이유는 아래와 같다.

Fully Connected Layer는 Dense Layer이다.
즉, 필요한 Dimension은 (Input 뉴런 개수 * Output 뉴련 개수)이다.
따라서, Fully Connected Layer의 Parameter 개수가 너무 커진다는 단점이 존재한다.
학습이 잘 진행되고 Generalization을 잘 하기 위해서는 Layer를 깊게 하고 Parameter 수를 적게해야 한다.
즉, Parameter가 기하급수적으로 커지는 Fully Connected Layer를 줄이는 것이다

CNN에서의 Parameter 개수

• Parameter 개수 : Kernel 크기 Input Channel Output Channel * Kernel 개수
  • Kernel 크기 : Convolution을 수행하는 Kernel 크기
  • Kernel 개수 : 가끔 Convolution에서 1개가 아닌 다수 Kernel을 동시에 활용하는 Case가 존재하고, 이 때 Kernel의 개수를 세서 곱해줘야 함
  • Input Channel : Convolution을 수행하기 위해서는 Kernel을 Channel만큼 복사하여 계층을 만들 필요가 존재하므로 Input Channel만큼의 Kernel이 필요함
  • Output Channel : 1개 Kernel을 통해 만들 수 있는 Output의 Channel은 무조건 1개이다. 따라서, Output Channel 개수만큼의 Kernel이 필요할 것이다.

Kernel 관련 용어

Stride

Kernel이 Input Data의 Convolution을 위해 움직일 Pixel 수를 말한다.

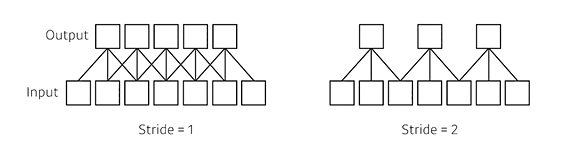
Padding

Side에 붙일 쓰레기 값 계층이다.
원래 이미지 등의 데이터 가장자리 값은 Kernel의 계산에서 많이 제외된다.
이를 방지하기 위해(가장자리 값도 Kernel에 대해 모든 연산을 수행하기 위해서) 쓰레기 값을 붙여 Convolution에 영향을 주지 않으면서 가장자리 값 계산을 수행하도록 하기 위해 활용한다

• zero padding : 붙일 쓰레기 값의 Data를 0으로 채움
  

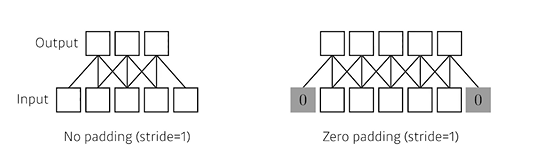
1 * 1 Convolution

1 X 1 X (Channel) 형태의 Kernel로 Convolution 하는 것을 의미한다.

• 목적
  • Dimension Reduction : Channel 방향으로 Dimension을 감소시킴
  • Convolution Layer를 깊게 쌓으면서 Parameter 수를 줄임
  • Bottleneck Architecture

---

CNN의 역사

간단한 특징

• VGG : Repeated 3 X 3 Blocks
• GoogLeNet : 1 * 1 Convolution
• ResNet : Skip-Connection
• DenseNet : concatenation
• 발전될 수록 Layer가 깊어짐

AlexNet

GPU 부족을 해결하기 위해 Network를 2개로 나누어 계산한 Model로써, 5 Convolution Layer & 3 Dense Layer를 가진다.

AlexNet은 몇 가지 특징을 지닌다.

ReLU 활성 함수 활용

• Linear Model의 특성을 유지해줌
• Gradient Descent를 통한 학습이 쉬워짐
• Good Generalization
• 기울기 소멸 문제의 해결에 효율적

Local Response Normalization

현재는 많이 활용되지 않는 기법으로, 측면 억제를 활용한 Normalization 방법이다.
특정 값이 주변 픽셀에 영향을 미치는 것을 밪이하기 위해 인접한 채널의 같은 위치에 존재하는 픽셀 n개를 정규화하는 것

Overlapping Pooling

Data Augmentation

Dropout 적용

VGGNet

모든 계층에서 3X3 Convolution Kernel만 활용한다는 특징을 가지며, Stride는 1로 설정하여 필요한 Parameter 개수를 최대한 줄이기 위해 노력했다.
또한 Fully Connected Layers에서는 Parameter를 줄이기 위해 1X1 Convolution Kernel 활용했다.

Dropout 활용했으며, vgg16, vgg19가 대표적인 Model이다.

GoogLeNet

1X1 Convolution을 적극적으로 활용하여 Parameter 개수를 줄인 특징을 가진 Model로써, Inception Block이라는 새로운 개념을 적용했다.

• 사진 출처 : https://norman3.github.io/papers/docs/google_inception.html

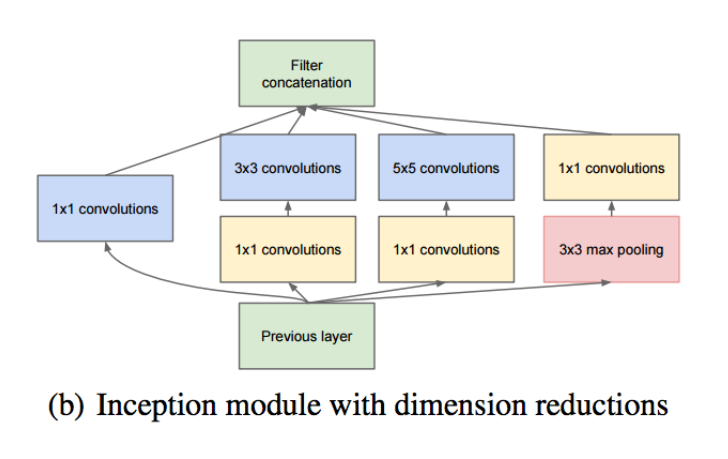
Inception Block은 Layer를 1X1 Convolution을 활용하여 Parameter 개수를 줄이고, 여러 계산을 통합하여 다음 Layer를 만드는 방식이다.

ResNet

Skip Connection(Identity Map) 활용한다는 특징을 가진 Model이다

Skip Connection이란 Convolution 이후 결과 값에 계산 이전 값을 더하여 활용하는 것을 의미하며, Output = f(x) + x 수식을 활용한다.

기존에 학습한 정보를 활용하여 추가적으로 학습하는 내용이 무엇인지 알 수 있게한 Model로써, 오픈북이 가능한 시험으로 생각하면 될 것이다.
여기서 책 = x, 시험 = f(x)으로 생각하면 될 것이다.

연산 과정

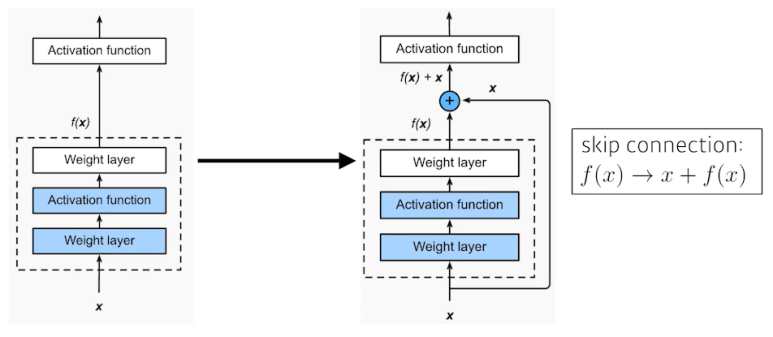
• 오른쪽 사진에 '+' 연산을 추가하여 f(x)를 f(x) + x로 변경시킴
• '+' 연산은 Identity Mapping으로써 f(x)와 f(x) + x의 Shape는 동일해야 함

Resnet 변형

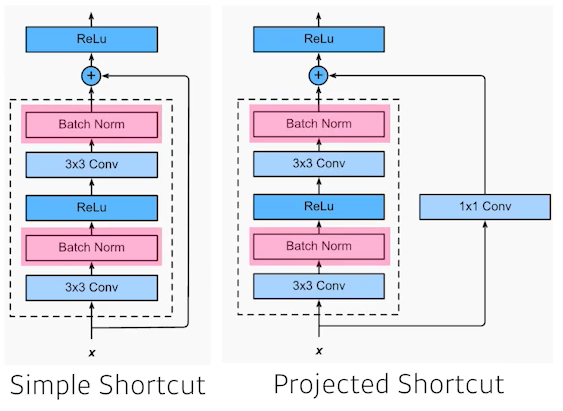
• Simple Shortcut : ResNet 구조에 BatchNorm 추가
• Projected Shortcut : x와 f(x)의 Dimension이 다를 경우를 대비해 1X1 Convolution을 추가하여 차원이 다른 Data끼리 연산이 수행되지 않도록 함
  • 가장 효율적인 Batch Norm의 위치에 대해서는 논란이 있음
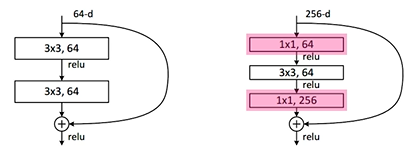
• Bottleneck Architecture
  • 목적 : Parameter 개수를 줄이기 위함
  • Convolution 수행 전에 Input Data를 1X1 Convolution으로 Channel을 줄이고 Convolution 수행 이후 1X1 Convolution을 활용해 다시 원래 Channel로 복구시키는 구조
    

DenseNet

ResNet에서 '+' 연산 대신 Concatenation으로 이전 Data들을 (List에) 담게 변형시킨 Model이다.

Concatenation을 활용하므로 Data Channel이 지수적으로 증가하며, Parameter를 줄여야 하므로 중간 중간 Transition Block을 통해 Channel을 줄이는 과정이 추가된다.

DenseNet의 Block은 Denses Block과 Transition Block이 존재한다.
Dense Block에서는 Channel이 Concatenation을 통해 증가하는 과정을 처리하며, Transition Block에서는 Data의 Channel 수를 줄이는 과정을 처리한다.
Transition Block에서는 Batch Norm -> 1X1 Convolution -> 2X2 AvgPooling 과정을 거쳐 데이터를 처리한다.

---

여러 가지 Image 처리 목적

Semantic Segmentation

• 공부했던 사이트 : https://kuklife.tistory.com/117
• Pixel이 속하는 Label 값을 출력하는 것
• 활용하는 이론 : FCN(Fully Convolutional Networks)
  • Fully Connected Layer(FCL)은 Image Segmentation에 적합하지 않으므로, FCL을 대체하는 방법으로써 활용하는 기법
  • 이유 : FCL을 활용하려면 Input이 고정되어 있어야 하며, FCL을 거치면 위치 정보가 사라지는데 FCL에서는 위치 정보가 중요하기 때문에(복원을 시켜야 하므로) 심각한 문제가 발생
  • FCL을 Convolution Layer 활용으로 대체
    • Input이미지가 커져도 Result dimension이 커질 뿐 동작이 가능
    • 위치 정보가 보존됨
  • Convolution Layer를 거친 이후 Heatmap을 활용하여 Segmentation 구현
• Deconvolution
  • Convolutio의 역연산
  • 추출된 Feature의 정보로부터 크기를 키워주는 역할 수행
    • Unsampling 방법
  • Convolution 과정을 통해 만들어진 Result(Heatmap)을 Deconvolution으로 다시 Unsampling 하여 처음 Input Data와 유사하게 복원시켜 Segmenatation Output을 얻는 것
    • (ex) 고양이가 있으면, 고양이를 Convolution으로 Unsampling한 이후 Heatmap을 얻는다. 이후 이 Heatmap을 활용하여 다시 고양이 형태와 유사하게 복원하는 과정을 말한다.

Detection

• 정의 : 이미지 내에 객체의 위치를 나타내는 Bouding Box를 그리고, Bounding Box에 해당하는 Object의 Label(종류)에 대해 찾는 문제
• 최근 가장 핵심적인 문제

---

Detection Algorithm

• RoI(Region of Interest) : 흥미가 있는 영역(내가 확인해 볼 영역;Region)
• 추가 공부를 위한 추천 사이트 : https://yeomko.tistory.com/13

R-CNN

• Data 처리 과정
  (1) 이미지를 Input으로 집어 넣음
  (2) Cropping : 여러 개의 Region(주로 2000개)를 Bounding Box로 뽑아 Selective Search Algorithm을 통해 추출하여 잘라냄
  (3) Warping : CNN 모델에 넣기 위해 모두 같은 사이즈로 만듬
  (4) 2000개의 Warped Image를 모두 CNN 모델에 넣어 각각 Classification을 진행하여 결과를 도출
• 단점
  • Image를 Warping 시키는 과정에서 이미지 변형으로 인한 손실 존재
  • CNN 모델에 모든 Data를 넣기 때문에 시간이 매우 오래 걸림
  • Selective Search나 SVM이 GPU에 적합한 구조가 아님
  • 뒤에서 수행한 Computation을 Share 하지 않아 Back Propagation이 없음

SPPNet

• 개념 : CNN을 한 번만 돌려 Detection을 수행하자
• Data 처리 과정
  (1) 전체 Image를 미리 학습된 CNN을 통과시켜 Convolution Feature Map을 추출
  (2) Selective Search를 통해 찾은 RoI들에 SPP를 적용하여 고정된 크기의 Feature Vector 추출
  (3) FCL에 통과시키고, 이를 통해 얻은 Vector로 이미지 클래스별 Binary SVM Classifier를 학습시킴
  (4) 추출한 Vector로 Boudnign Box Regressor를 학습시킴
• 단점
  • End-to-End 방식이 아니므로 학습에 여러 단계가 필요함
  • Selective Search의 이용
  • 학습 과정에서 Conv Layer들은 학습시키지 못함

Fast R-CNN

• Data 처리 과정
  (1) 전체 이미지를 미리 학습된 CNN에 통과시켜 Convolution Featue Map을 추출
  (2) Selective Search를 통해 찾은 각각의 RoI에 대해 RoI Pooling을 진행하여 고정된 크기의 Feature Vector를 얻음
  (3) Feature Vector는 FCL들을 통과하여 2개 Branch로 나뉨
  • softmax 브랜치 : 해당 물체의 Label을 Classification
  • bbox regressor 브랜치 : bounding box regression을 통해 Selective Search로 찾은 박스의 위치를 조정
• 단점
  • 아직도 시간이 오래 걸림
  • Bottleneck이 발생할 수 있음

Faster R-CNN

• 개념 : Fast R-CNN에서 Selective Search 대신 RPN을 활용

• 미리 정해 놓은 Detection Box인 Anchro Box를 준비해 활용

• RPN(Region Proposal Network)
  (1) CNN을 통해 Feature Map을 생성하고, 입력으로 받음(크기 : H X W X C)
  (2) Feature Map에 3X3 Convolution을 256 or 512 Channel만큼 수행. 이 때 H와 W는 유지시켜 두 번째 Feature Map을 얻는다
  (3) 두 번째 Feature Map으로 Classification과 Bounding Box Regression 예측값을 계산한다. 이 때 FCN의 특징을 가진다(Size에 Independent한 알고리즘이 필요함)

  • Classification Result : 1X1 Convolution을 (2*Num.Anchor) Channel만큼 준비
  • Bounding Box Regression Result : 1X1 Convolution을 (4*Num.Anchor) Channel만큼 준비

  (4) Classification을 통해 특정 물체일 확률 값을 정렬하고 확률이 가장 높은 순으로 K개의 Anchor 선택
  (5) K개의 Anchor에 대해 Bounding Box Regression을 적용한다. 이 때 (3)에서 얻은 값들을 활용한다
  (6) Non-Maximum-Supression을 적용하여 RoI를 구해줌

YOLO

• S X S Grid로 나누고, 물체의 중앙이 해당 Grid에 들어가면 Box를 지정하고 동시에 Label 예측까지 수행해줌

  • 동시에 두 작업을 수행하고 마지막에 두 정보를 취합함

• Bounding Box Sampling이 필요 없음

• Data 처리 과정
  (1) S X S grid로 공간을 쪼갬
  (2-1) grid의 cell(box) 값을 통해 Bounding Box를 예측함

  • Confidence, Box Refinement(x,y,w,h) 값을 활용하여 예측
  • box refinement
    • (x,y) : Bounding Box의 중심점 좌표
    • w : 너비
    • h : 높이
  • Box Refinement를 활용하여 Confidence를 계산하고, 이를 활용해 Bounding Box 예측

  (2-2) 각 Cell이 의미하는 객체가 무엇인지를 고려하여 Class 개수를 나눔

  • (2-1), (2-2) 과정이 동시에 수행됨

  (3) 결과적으로 S X S X (B*5 + C) Size의 Tensor가 형성되며, 이 Tensor를 활용하여 학습 진행

  • S X S : Grid 공간
  • B : 예측한 Bounding Box 개수
  • C : Class 개수