Bag of Words(BOW)

Bag of Words란?

단어들의 순서는 전혀 고려하지 않고, 단어들의 출현 빈도에만 집중하여 Text Data를 수치화하는 방법이다.

각 단어들에 고유한 정수 인덱스를 부여한 뒤, 단어 Token의 등장횟수를 해당 단어에 부여된 index에 저장하여 Bag of Words를 생성한다.

Bag of Words 구현 과정

• John really really loves movie를 예시로 설명

Step 1 : Unique한 단어들을 모아서 Vocabulary를 구축

• Vocabulary : List 형식에 단어들을 "한 번 씩"만 나오도록 저장
• (ex) Vocabulary : {"John", "really", "loves", "movie"} -> really는 2번 나오지만 중복 없이 List를 구성해야 함

Step 2 : 각각의 단어를 One-hot vector로 형성함

• Step 1에서 구현한 Vocabulary를 활용하여 각각의 단어와 index(Dimension)을 Mapping함
• 모든 단어 사이의 Euclidean distance는 $\sqrt{2}$이며, cosine similarity는 0
  • 실제 단어 구조 및 의존성과 관계없이, Bag of words에서 모든 단어들은 동일한 관계를 가지는 Vector로 표현됨
• (ex) John : [1, 0, 0, 0], really : [0, 1, 0, 0], loves : [0, 0, 1, 0], movie : [0, 0, 0, 1]의 One-hot vector로 형성

Step 3 : Bag of Words 생성

• Sentence/Document의 모든 단어에 대한 One-hot vector를 더하여 최종 Bag of words Vector를 형성
• (ex) John, loves, movie는 1번씩, really는 2번 더해지므로, 최종적으로 [1, 2, 1, 1]의 Bag of Words를 형성할 수 있음

---

Naive Bayes Classifier

Naive Bayes Classifier란?

Bag-of-Words를 활용하여 정해진 Class 중의 하나로 분류할 수 있는 대표적 방법이다.
Bayes' theorem을 이용하여 텍스트 분류를 수행하는 Classifier로써, 토큰화 이전 단어의 순서는 중요하지 않다. BoW와 비슷하게 단어의 순서나 관계를 무시하고 오직 빈도수만을 고려하는 Classifier이다.

Naive Bayes Classifier의 Decision Rule은 MAP(Maximum A Posterior)로써, most likely class를 찾는 것이다.
즉, 해당 Document가 속할 것이라고 예측되는 Label(클래스)을 찾는 것이다.

Naive Bayes의 수식적 이해

• Document d가 존재하고, 이 document 내에 여러 개의 클래스(Label) c가 존재하며, 모든 클래스 c의 합집합을 C라고 가정하자

MAP에 관련된 수식

• 첫번째 줄 : $c_{MAP}$의 개념
• 두번째 줄 : Bayes Rule의 적용
• 세번째 줄 : 우리는 Document d에 대해서만 판단할 것이기 때문에, P(d) = 1로 가정
• P(d|c) : Category(Class)가 고정되었을 때 문서 d가 나올 확률

위에서 P(d|c)는 Category가 고정되었을 때 문서 d가 나올 확률이라고 하였다. 그리고 세번째 줄에서 P(d) = 1로 고정되었다.
둘이 모순적이지 않은가?

이는 기준점의 차이에 있다고 생각한다.
결국 P(d|c)는 결국 Document 내에 존재하는 모든 개별의 단어에 대해 Class 여부를 판단하여야 한다. 즉, 문서 d가 나올 확률이라고 말하였지만 정확히 말하자면 문서 d에 존재하는 단어가 c일 확률을 구하는 것이다.
하지만 P(d)는 실제로 내가 판단하는 문서가 d인가?를 물어보는 확률이기 때문에, P(d) = 1로 설정한 것이다.

MAP 수식의 발전

• $w_i$ : Document에 존재하는 i번째 단어

Conditional Independence Assumption을 적용한 수식이다.
Naive Bayes Classifier는 위에서 말했듯 단어 사이의 관계 등을 무시하고 오직 빈도수만을 생각하기 때문에, $w_1$ 단어와 $w_2$ 단어는 서로 독립적인 관계이다

위 수식을 $c_{MAP}$에 적용하면 최종적으로 위 P(d|c)P(c) 값을 가장 크게 만드는 c를 찾으면 될 것이고, 이것이 Naive Bayes Classifier가 하는 일이다.

---

Word Embedding

Word Embedding이란?

단어를 특정 차원의 Vector로 표기하는 기법이다.

서로 Similar한 단어이면 Short distance, 비슷하지 않을 경우 Far distance를 가지도록 Vector를 형성하며, BoW와는 달리 단어들 사이의 관계까지 고려 할 수 있는 방법이다.

Word2Vec

Word2Vec이란?

같은 문장에서 나타난 단어들은 유사할 것이라는 가정으로 수행되는 알고리즘으로, NNLM의 느린 학습 속도와 정확도를 개선하여 탄생한 알고리즘이다.

NNLM은 Word Embedding의 개념을 처음 도입한 모델로써, NNLM은 Projection Layer에서 한 개의 Hidden Layer를 더 거치지만, Word2Vec은 그 과정을 생략했다는 특징을 가진다.
또한 NNLM은 이전 단어들만을 참조, Word2Vec은 전후 단어 모두 참고한다는 차이점을 가진다.

Word2Vec은 단어들을 Vector로 표시한 것이기 때문에, (충분한 학습이 진행된 이후) 특정 Vector를 더하거나 빼서 다른 단어를 유도할 수도 있다.
예를 들어, "한국 - 서울 + 파리" 연산으로 "프랑스"라는 결과 단어를 출력할 수 있다.
또한, Hidden Layer(Projection Layer)가 1개인 얕은 신경망으로 구현되어 활성화 함수가 없고, 단순히 W(가중치 행렬) 2개만 존재하는 Model이다.

Word2Vec의 학습 방식

CBOW(Continuous Bag of Words)와 Skip-gram 2가지 방식이 존재한다.

CBOW는 주변에 있는 단어들을 입력으로 중간에 있는 단어를 예측한다.

Skip-gram은 중간에 있는 단어들을 입력으로 주변에 있는 단어들을 예측한다.

메커니즘 자체는 매우 유사함을 알 수 있다.

Word2Vec 수행 과정(CBOW)

• 사진 출처 : https://wikidocs.net/22660

1. 윈도우(Window) 설정

• 윈도우 : 중심 단어를 예측하기 위해 앞뒤로 몇 개의 단어를 볼지 정하는 (탐색) 범위
• 윈도우 크기를 n으로 설정했다면, 실제 중심 단어를 예측하기 위해서는 앞의 n개, 뒤의 n개를 고려하여 총 2n개의 단어를 활용한다.

2. 학습 Data를 Word별로 분리(Tokenization) & Vocabulary 만들기

• Vocabulary를 활용하여 단어별 One-hot Vector를 형성함(BoW와 동일)

3. Sliding Window 기법을 적용하여 학습을 위한 데이터 셋을 만듦

• Sliding Window : 윈도우를 옆으로 움직여 중심 단어를 변경해가며 여러 가지 Data를 만드는 것
• Input : Window 크기로 인해 설정된 주변 단어들
  Output : 중심 단어
  

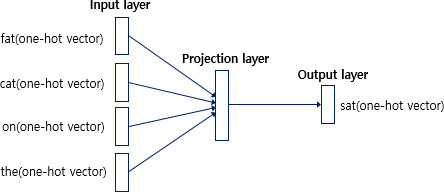
4. 입출력 쌍을 처리하기 위한 2-Layer 구조를 만듦

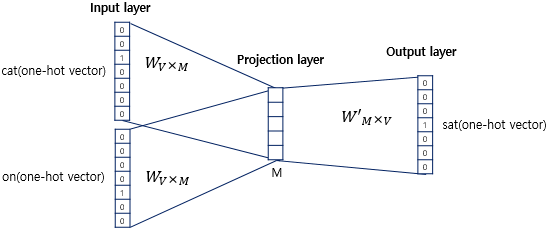
• Hidden Layer의 Node 수는 인간이 직접 정해주고 학습이 진행됨

5. 모든 주변 단어(Input)에 대하여 $W_{V X M}$을 곱해주고, 이렇게 나온 다수의 Vector들을 합침

• 수행되는 연산 : v = $\frac{\sum{V_{주변 단어}}}{2 X N}$
• 위에서 연산으로 써서 복잡해보이지만, 그냥 모든 단어에 행렬을 곱해주고 결과값의 평균을 구하면 됨
• 우리는 Projection Layer에 최종적인 연산이 수행된 v를 활용함

6. Projection Layer에 저장된 v를 $W_{M X V}'$와 곱해줘 z Vector를 구하고, 해당 Vector에 softmax 연산을 수행하여 최종적인 결과값을 구함

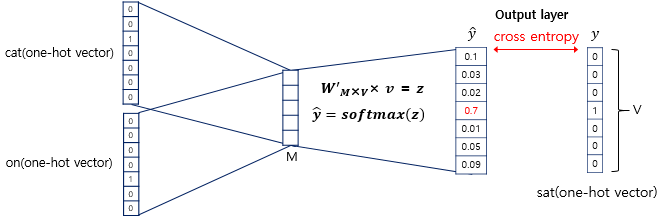
• Loss Function으로 크로스 엔트로피(cross-entropy) 함수를 활용
• softmax(z)로 나온 스코어 벡터를 one-hot vector 결과값인 y와 최대한 비슷하기 위해 크로스 엔트로피 활용

추가적 설명

• 수행되는 연산 : y = softmax($W_2W_1$x)
  • x : Input
  • y : Model 예측한 y
  • $W_2$ : Output을 도출하는 가중치 행렬
  • $W_1$ : Input을 도출하는 가중치 행렬

CBOW의 핵심은 Input, Output을 활용하여 2개의 가중치 행렬을 조금씩 조정하는 것이다.
Input, Output vector의 내적 값이 커지도록 학습이 진행되는데, 내적 값이 크다는 것은 유사한 위치에 Vector들이 존재한다는 의미이며, 이는 유사성이 크다는 것을 의미한다.

Skip-gramdptjsms CBOW의 평균을 구하는 과정은 존재하지 않으나, 대신 Output Layer를 도출하는 가중치 행렬이 많아야 한다.
일반적으로 Skip-gramdl CBOW보다 성능이 좋다고 알려져 있다.

Softmax 연산을 활용하고, 나중에는 Negative Sampling이라는 기법도 활용했다.
Negative Sampling이란 학습 과정에서 전체 단어 집합이 아니라 일부 단어 집합에만 집중할 수 있도록 하는 방법이다.
Window에 존재하는 단어들과 윈도우 내에 등장하지 않는 단어(Negative Sample) 5 ~ 20개를 뽑는다. 이후, 위 단어들을 모두 합쳐 집중할 단어(Positive Sample)을 1로, Negative Sample을 0으로 Labeling한 이후 Word2Vec 과정을 수행하는 것으로써, Unsupervised Learning을 Classification Task로 바꾸는 역할을 해준다.

Instrusion Detection

여러 단어들 중 의미가 상이한 단어를 찾아내는 Task이다.
예를 들어 dog cat tree일 경우, tree는 식물이고 나머지는 동물이므로 tree를 찾는 Task이다.

Word2Vec이 학습한 Embedding Vector를 활용하여 수행 가능한데, Euclidean distance를 자기 자신을 제외한 모든 단어에 대하여 구하고, 이 값의 평균을 모든 단어마다 계산한다.
이후, 계산된 평균값 중 가장 큰 값을 가지는 단어를 Select하는 방식으로 구현할 수 있다.

Word2Vec의 활용 영역

• Word Similarity
• Machine Translation
• PoS Tagging
• NER
• Sentiment analysis
• Clustering
• Image Cpationing

GloVe

GloVe란?

Word2Vec, LSA의 단점을 지적하며 나온 Model이다.

Word2Vec은 단어 벡터 사이의 유사도를 측정하는데는 좋지만, 사용자가 지정한 Window 내에서만 학습이 진행되므로 말뭉치 전체의 co-occurence는 반영되기 어렵다(예측 기반)
LSA는 말뭉치 전체의 통계적 정보를 활용하지만, 단어/문서간 유사도를 측정하기는 어렵다(카운터 기반)

여러 연구에서 GloVe가 Word2Vec보다 무조건 좋은 성능을 보이는 것은 아니라고 알려졌기 때문에 두 방법 모두 활용해보고 더 속도가 빨라지는 Word Embedding 방식을 활용해야 한다.

GloVE는 어떤 단어쌍이 동시에 등장한 횟수를 미리 계산하여, 이 계산값에 log를 씌운 이후 내적값의 Ground Truth로 활용하여 학습을 진행한다.
이 때 전체 말뭉치의 모든 단어에 대하여 동시 등장 확률을 계산하는데, 동시 등장 확률이란 학습 말뭉치에서 동시에 등장한 단어의 빈도를 세어 전체 말뭉치의 단어 개수로 나눠준 값이다.
즉, Document에 두 단어가 얼마나 동시에 등장하였는지에 대한 비율을 말한다.

GloVE는 단어쌍이 동시에 등장한 횟수를 미리 계산하였으므로 중복된 계산이 줄어들어 Training이 빠르게 진행된다.
또한 적은 Data에 대해서도 잘 학습한다는 장점을 가진다.

하지만, 미리 Co-occurence 행렬을 만들어야 하기 때문에, 계산 복잡성이 크며 행렬을 저장할 메모리도 많이 필요하다는 단점을 가진다

GloVe 목적 함수 유도

• 참조 : https://ratsgo.github.io/from%20frequency%20to%20semantics/2017/04/09/glove/

1. 찾고자 하는 것 : 임의의 함수 F

• $P_{ik}$ : P(k|i). i번째 단어 주변(Window Size내)에 k번째 단어가 등장할 조건부 확률

2. $w_i, w_j, w_k$간의 관계를 따지기 위해 $w_i, w_j$를 뺀 벡터와 $w_k$를 내적
& $P_{ik} = F(w_i^T\tilde{w_k})$로 정의

• $P_{ik}$는 $w_j$가 존재하지 않으므로, $w_j = 0$인 F를 고려하면 위 수식이 유도됨
  $F(w_i^T\tilde{w_k} - w_j^T\tilde{w_k}) = \frac{F(w_i^T\tilde{w_k})}{F(w_j^T\tilde{w_k})}$

3. 위 F는 아래 3가지 조건을 만족해야함

• $w_i$와 $w_k$를 바꾸어도 F는 같은 값을 반환해야 함
  • 이유 : 중심 단어는 언제든 바뀔 수 있으므로
• Co-occurence Matrix(동시 등장확률으로 만든 Matrix)는 Symmetric Matrix이고, F는 이를 반영 해야함
  • 이유 : (A, B)단어의 동시 등장확률과 (B,A) 단어의 동시 등장확률은 같아야만 함
• homomorphism 조건을 만족해야 함
• 위 3가지 조건을 만족시키기 위하여 F를 지수함수($e^x$; exp)로 치환함

4. 유도되는 수식

• F를 exp로 변환시키고, 양변에 $F(w_j^T\tilde{w_k})$를 곱해준 이후 log를 씌워주면 유도 가능
• $X_{ik}$ : i번째 단어와 k라는 단어가 동시에 등장한 빈도수
• $P_{ik} = P(k|i) = \frac{X_{ik}}{X_i}$이므로 유도되는 수식

5. 문제는 위 수식으로 유도하면 $logX_i$ 부분 때문에 $w_i, w_k$를 바꾸면 값이 달라진다. 이는 위 3번에서 말했던 F가 만족해야 할 조건을 위반하는 것이므로, $logX_i$를 $b_i, b_k$라는 상수항으로 처리해 조건을 만족하도록 했다.

6. 구한 수식 중 $X_{ik}$ 값은 정해져 있는 값이고, 좌변은 미지수이므로 둘의 차이를 최소화하는 것이 목적 함수 J의 최종적 목표가 될 것이다.

• J를 최소화하는 $w_i, w_j, b_i, b_j$를 구하는 것이 최종적 목표
• V : 전체 단어 개수

7. $X_{ij}$가 특정 값 이상으로 너무 커지는 경우(지나치게 빈도가 높게 나타나는 단어)를 방지하기 위하여 f(x)를 추가하여 최종 목적함수를 만들었다

• f(x) = $\frac{x}{x_{max}}^a$ if x < $x_{max}$
  f(x) = 1 otherwise