여러 가지 차트

DONGJIN IM·2022년 2월 21일

데이터 시각화

목록 보기

2/6

Bar Plot

Bar Plot이란?

직사각형 막대를 사용하여 데이터 값을 표현하는 차트(그래프)
Category에 따른 수치 값을 비교하기에 적합한 방법
Bar 사이 Gap이 0이라면, histogram(.hist())를 활용
그룹이 5 ~ 7개 이하일 경우 효과적 ⇒ 수가 적은 그룹을 ETC로 처리
막대 방향에 따른 분류
- 수직(Vertical) : x축에 범주, y축에 값을 표기
- 수평(Horizontal) : y축에 범주, x축에 값을 표기
  - 범주(Category)가 많을 때 적합
모양에 따른 분류
- Multiple Bar Plot : 여러 개의 Bar Plot을 그리는 것
- Stacked Bar Plot : 2개 이상의 그룹을 쌓아서 표현하는 Bar Plot
  - 그룹이 2개일 경우, positive/negative로 축 조정 가능
  - Percentage Stacked Bar Chart : 비율을 계산하여 만든 Stacekd Bar Plot
- Overlapped Bar Plot : 겹쳐서 그리는 Bar Plot
  - 3개 이상의 그룹이 존재할 경우 사용하지 않는 것이 좋음
  - 같은 축을 활용하기 때문에 비교가 쉬움 ⇒ alpha를 통해 투명도 조정으로 겹치는 부분 파악
- Grouped Bar Plot : 그룹별 범주에 따른 Bar를 이웃하게 배치하는 방법
정확한 Bar Plot 그리기
- 데이터 정렬하기
  - 시계열 : 시간순, 수치형 : 크기순, 순서형 : 범주순, 명목형 : 범주값에 따라 정렬
  - Dashboard에서는 Interactive로 제공하는 것이 유용
  - Pandas의 sort_values(), sort_index()를 활용
- 여백과 공간을 적절히 조정하여 가독성을 높임
- 필요 시 격자를 추가하거나, 축 숫자를 조정하거나, Text를 추가하여 가독성을 높임
- 오차 막대를 추가(errorbar)

코드로 보는 Bar Plot

Bar Plot 그리기

x = np.array([1,2,3,4,5]) # Category를 의미함
y1 = np.array([1,3,5,3,1]) # Value1
y2 = np.array([2,4,6,8,10]) # Value2

ax[0].bar(x,y1)  # 수직 Bar Plot
ax[1].barh(x,y2) # 수평 Bar Plot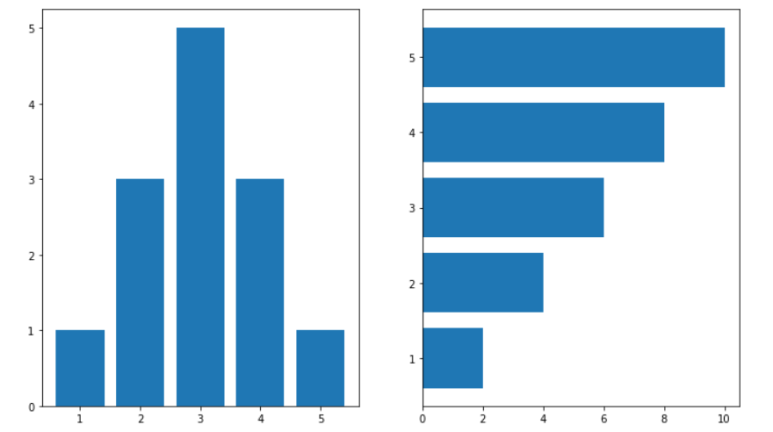

설명
수평 Bar Plot에서 ndarray의 가장 앞쪽의 값이 그래프의 가장 아래쪽에 존재하는 
것을 볼 수 있다.(1이 가장 아래에 존재) 
하지만 수평 Bar Plot의 경우 대부분 맨 위에 1부터 시작하는 것을 선호하기 때문에 
sort에 대한 Function을 수행하되 ascending=False로 지정하여 내림 차순으로 
정렬시키는 경우가 많다

y축의 Size를 동일하게 만들기(이유 : Principle of Proportion Ink를 지키기 위해)

방법 1 : 한 번에 모든 Ax size를 맞추기

# 방법 1 : 한 번에 모든 Ax size를 맞추기
fig, ax = plt.subplots(1,2, sharey=True) 
# sharey Parameter 값을 True로 설정하면 subplots로 만들어지는 모든 Ax의 y축 
# size는 동일함
# sharex = True를 통해 x축 크기도 일치 시킬 수 있음

x = np.array([1,2,3,4,5])
y1 = np.array([1,3,5,3,1])
y2 = np.array([2,4,6,8,10])

ax[0].bar(x,y1)
ax[1].bar(x,y2)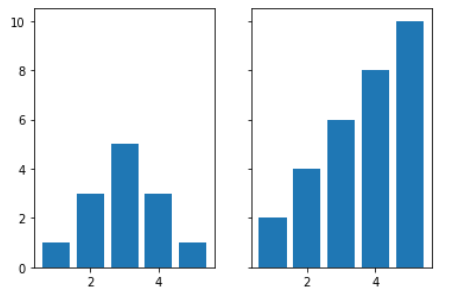

방법 2 : 모든 Ax에 대해 y축의 size를 직접 지정해주는 방식

set_ylim(최솟값, 최댓값) : 최솟값과 최댓값의 범위만큼 y축 size가 지정됨

fig, ax = plt.subplots(1,2, figsize=(12,7))

for sub_ax in ax:
    sub_ax.set_ylim(0,15)

 x = np.array([1,2,3,4,5])
 y1 = np.array([1,3,5,3,1])
 y2 = np.array([2,4,6,8,10])

 ax[0].bar(x,y1)
 ax[1].bar(x,y2)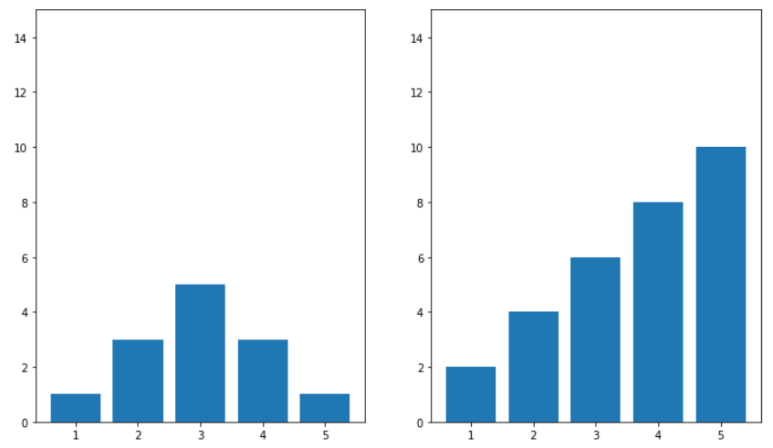

Stacked graph 생성

x = np.array([1,2,3,4,5])
y1 = np.array([1,3,5,3,1])
y2 = np.array([2,4,6,8,10])

ax[0].bar(x,y2, bottom = y1)
ax[0].set_title("Only y2")
# botttom Parameter를 활용하여, 아래에 깔(Stack 시킬) Data 값을 입력한다
# 위 예시에서는 y1을 Bottom으로 설정했으니, Bottom만큼 빈 공간으로 만든 뒤 
# y2에 대한 Bar Plot을 그린다

ax[1].bar(x,y2, bottom = y1)
ax[1].bar(x,y1)
ax[1].set_title("y1 AND y2")
# 위와는 다르게, y1에 대한 Bar Plot도 그렸기 때문에 
# Stacked Graph로 생성이 되었을 것이다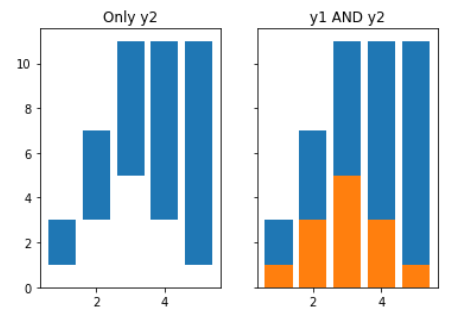

Grouped Bar Plot 그리기
Bar가 존재해야 하는 위치 공식 : $x + width * \frac{(-N+1+2*index)}{2}$

width : (Bar의) 너비
x : x축 값
N : 총 Graph 개수

index : 몇번째 그래프를 그리는가

width = 0.2
N = 2       

def f(idx, x):
    return x + width * ((-N+1+2*idx)/2)
# Bar 1개당 존재해야 하는 위치값을 반환

fig, ax = plt.subplots(1,1, sharey=True) 

x = np.array([1,2,3,4,5])
y = np.array([[1,3,5,3,1], [2,4,6,8,10]])

for idx in range(N):
    ax.bar(f(idx, x), y[idx], width = width)
    # idx번째 그래프에 대한 위치를 구한 뒤 Bar Plot을 구함

plt.show()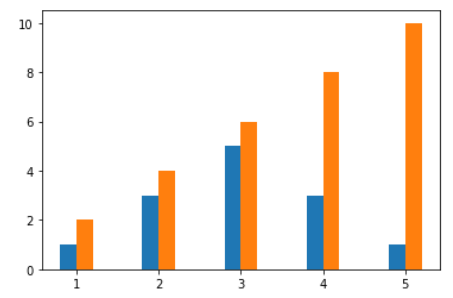

기타 Bar Plot Parameter

fig, ax = plt.subplots(1,1, sharey=True) 

x = np.array([1,2,3,4,5])
y = np.array([1,3,5,3,1])

ax.bar(x,y,
      width = 0.3,           # Bar Plot의 너비에 대한 Paramter : width
      linewidth = 2,         
      # Bar Plot "테두리" 너비에 대한 Parameter : linewidth
      edgecolor = 'r',       
      # Bar Plot "테두리" 색깔에 대한 Parameter : edgecolor
      )

ax.bar(x,y,color='black', alpha=0.2)  
# Bar의 투명도에 대한 Parameter : alpha -> 0 ~ 1 사이의 값

for value in ['top', 'right']:
    ax.spines[value].set_visible(False)
"""
Ax의 테두리 없애는 메서드 : .spines[S].set_visible(False)
주로 top과 right을 지우는 경우가 많음

이전 강의의 spines 참조
"""

ax.grid(zorder=0)
# Grid 추가. 하지만 Text를 추가하는 것을 더 추천함
# zorder : 차트를 그릴 때 바깥쪽에 그려지는 차트일 수록 zorder 값이 커야함
    
plt.show()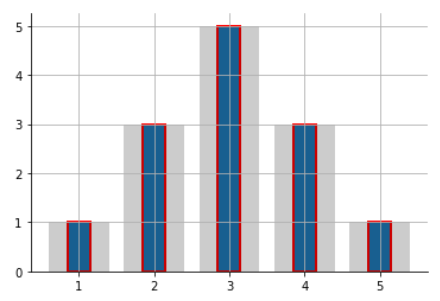

Errorbar 나타내기

모든 그래프에서 동일하게 활용 가능
코드 및 자세한 정보 : https://codetorial.net/matplotlib/errorbar.html
yerr Parameter 활용
- yerr에 들어온 값을 더한 것이 최대 오차, 뺀 것이 최소 오차가 됨
- yerr을 2*N 데이터로 입력하여 편차를 비대칭으로 표시할 수 있음
  - 첫번째 값이 아래 방향 편차, 두 번째 값이 위 방향 편차를 나타냄
  - yerr=[(2),(4)]로 지정할 경우, 오차 범위는 x-2 ~ x+4가 Errorbar로 표현됨*
capsize Parameter를 활용하여 Errorbar의 최대, 최소 위치에 가로선을 그어줄 수 있음
수학적 의미를 고려하면, yerr에는 Varaiance 값이 들어가는 것이 가장 좋음

Line Plot

Line Plot이란?

연속적으로 변화하는 값을 순서대로 점으로 나타낸 이후, 선으로 연결한 차트
시간/순서에 따라 변화하는 Data에 적합 ⇒ 추세(Trend)를 살피기 위해 사용
5개 이하의 선 사용을 추천
- 색상, Marker, 선의 종류 등을 통해 여러 개의 선 구분
- Marker : Point을 점이나 삼각형 등으로 체크하는 것
Noise의 인지적인 방해를 줄이기 위해 Smoothing 활용
Bar Plot과 달리 잉크의 원칙을 지키지 않아도 됨
Trend 관찰이 목표이므로, 이에 방해되는 Grid, Annotation을 줄이는 것을 추천
Graph 상에서 간격을 규칙적으로 해줘야 함
- 만약, 입력 데이터가 규칙적인 간격을 가지지 않는다면 Marker를 통해 관측값을 점으로 표시하여 추측 Data에 대한 오해를 줄여야 함
추가하면 좋을 것
- 라인 끝 단에 Label을 추가하면 식별에 도움이 됨
- Min/Max, 혹은 원하는 포인트에 대한 정보를 추가하면 가독성이 높아짐
- 단, Interactive하게 하거나 정보가 추가된 차트, 추가되지 않은 차트 2개를 제공하는 것을 추천
- 보다 연한 색을 활용하여 Uncertainity 표현 가능 ⇒ 신뢰 구간, 분산 등
사용을 지양하지만 알아둬야 하는 것
- 보간 : 점과 점 사이에 데이터가 없는 부분을 잇는 방법
  - Presentation 때는 Smoothing이 좋을 수도 있지만, 작은 차이를 없앨 수 있고 없는 데이터를 있다고 착각하게 만들 수 있으므로 일반적인 분석에서는 지양하는 것이 좋음
  - 방법 : Smoothing, Moving Average
- 이중 축 : 1개 Plot에 2개 축(dual axis)를 만들어 Plot을 그림
  - 종류 : 같은 시간 축에 대해 다른 종류의 데이터를 표현하는 이중 축, 한 개 데이터에 대해 다른 단위에 대한 축을 생성하는 이중 축
  - 2개 Plot을 그리는 것이 더 좋음

코드로 보는 Line Plot

Line Plot 그리기

x = np.arange(1,6)
y = x**2

ax.plot(x,y)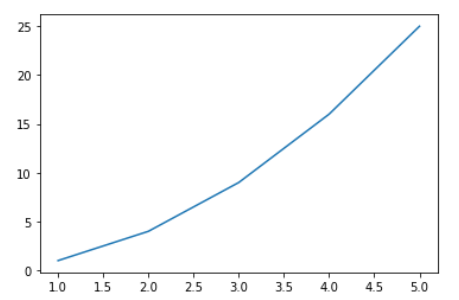

정 N각형 그리기(몰라도 된다. 신기해서 넣어봤음)

x = np.sin(np.linspace(0,2*np.pi, n))
y = np.cos(np.linspace(0,2*np.pi, n))

ax.plot(x,y)
# 결과적으로 정 (n-1)각형이 만들어진다
# n이 매우 커지면 원과 매우 유사하게 된다(아래 출력 결과는 n=4일때의 결과)

Line Plot에 대한 Parameter
- marker : 실제로 존재하는 Data에 Mark 표시를 해줄 때, 어떤 모양으로 Mark할 것인지 결정
  - .(작은 원), o(큰 원), *(별), ^(삼각형) 등
- linestyle : 데이터 사이를 잇는 Line 모양
  - solid(직선;'-'), dashed(짧은 직선 여러개; '--'), dashdot(짧은 직선과 점이 반복됨;'-.'), dotted(점으로 구성됨;':'), None(선을 그리지 않음)
- color : Line 및 Marker 색 지정

x = np.arange(1,21)
y = np.random.rand(20)

ax.plot(x,y,
       color='gray',       
       marker='*',         
       linestyle='solid'
       )

이중축
Case 1 : x축에 관련된 index는 동일하지만, Data 자체가 다름

x = np.arange(1,21)
y = np.random.rand(20)
z = np.random.rand(20)+ 20

ax.plot(x,y, color = 'red', label='Main')
ax.legend()
# 먼저, 내가 원래 그릴 Line Plot을 그림

ax2 = ax.twinx() 

# .twinx() 명령어를 통해 새로운 ax를 생성함. 
# twin에서 예측할 수도 있었겠지만, 쌍둥이처럼 같은 공간에서 그려지되, 
# 자신만의 y축 값을 가지고 있는 것이다. x축 값은 공유한다
ax2.plot(x,z, color = 'blue', label = 'Add')
ax2.legend()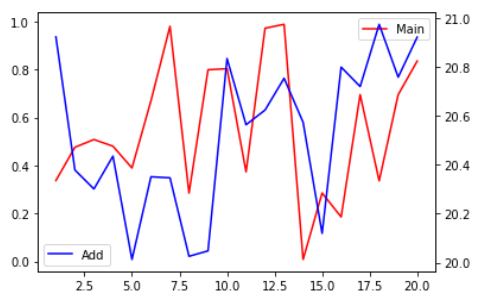

Case 2 : Data 자체는 같지만 단위 등을 다르게 표현하는 방법
- six(x)를 표현할 때, radian을 활용한 pi값으로 계산하는 방법이 존재할 것이고, degree(각도)로 계산 하는 사람도 있을 것이다. 따라서, degree와 Radian 2개의 단위를 모두 표현한 sin(x)를 그려보자
- 코드 출처 : https://matplotlib.org/stable/gallery/subplots_axes_and_figures/secondary_axis.html

def deg2rad(x):               
# degree -> Radian으로 바꾸는 함수
    return x * np.pi / 180

def rad2deg(x):               
# radian -> degree로 바꾸는 함수
    return x * 180 / np.pi

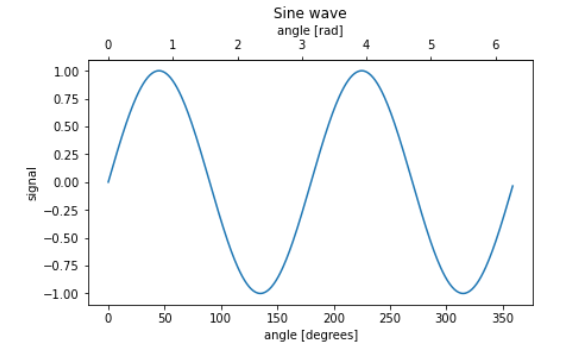
fig, ax = plt.subplots(constrained_layout=True)
x = np.arange(0, 360, 1)
y = np.sin(2 * x * np.pi / 180)
ax.plot(x, y)
ax.set_xlabel('angle [degrees]')
ax.set_ylabel('signal')
ax.set_title('Sine wave')
// 먼저, degree 값을 통한 sin(x) 그래프를 그린다

secax = ax.secondary_xaxis('top', functions=(deg2rad, rad2deg))
"""
이후, x축을 secondary_xaxis를 통해 하나 더 추가해준다.
'top' : 추가할 x축의 위치를 표현하는 것이다. 이외에도 'bottom', 
         y축일 경우 'left', 'right'이 가능하다
functions : 추가할 x축에 대해 값을 대응시켜주는 것이다
            예를 들어, 180도 일경우 Radian에서 파이의 위치와 매치시켜줘야 
            할 것이다. 이를 위한 함수이다
            첫번째 함수는 원래 그렸던 x값 -> 추가할 함수의 x값,
            두번째 함수는 추가할 함수의 x값 -> 원래 그렸던 x값으로 전환해주는 
            Function을 입력해준다
            이 Case의 경우 "먼저" 그렸던 x값은 Degree였으므로, 
            deg2rad을 첫번째 함수로 지정하였다
"""
secax.set_xlabel('angle [rad]')
# x축을 추가했고, 추가한 "x축"에 대하여 Label을 붙였다

plt.show()

"""
아래 결과 그래프를 보면, Data 자체는 sin(x)로 동일하지만 위에는 Radian 단위로, 
아래에는 Degree 단위로 설정되어 있음을 볼 수 있다. 
Function을 통해 매칭시켰으므로, 한 x축의 값을 다른 단위로 전환시켜보면
다른 x축의 값과 동일한 값이 도출될 것이다
"""

강조 표현 : Scatter, Plot, Text 등을 활용하여 표기해줌
Moving Average(이동 평균)
- 차례로 N개의 데이터를 묶어 평균을 냄
- N = 3일 경우, (1,2,3)의 평균, (2,3,4)의 평균, ...으로 Data를 전처리함
- 그래프의 Trend에 집중할 수 있게 해주는 Noise를 지워주는 대표적인 방법이다
- 이동 평균을 수행하기 위해서는 Data의 Type은 DataFrame이여야 함

# Data 전처리
x = np.arange(0,1,0.01)
y = pd.DataFrame(np.random.rand(x.shape[0]))

y = y.rolling(window=3).mean() 
# (과거 + 현재) 인접한 3개 데이터를 묶어, 그 평균을 낸 값으로 DataFrame을 생성
y.head()

설명
위에서 말했듯, rolling에서 window를 지정하면 해당 개수만큼 데이터를 묶어서 새로운
DataFrame을 형성하는 것이다
즉, 첫번째 값과 두번째 값은 (-1,0,1), (0,1,2) Data를 뽑을 수는 없기 때문에 
평균도 존재하지 않는다
따라서, 0,1 값은 NaN이 되는 것을 아래 결과에서 확인할 수 있을 것이다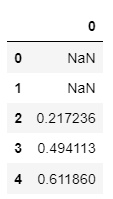

이동 평균을 활용하여 그래프의 Trend 파악을 쉽게한 방법

fig, ax = plt.subplots(1,2, figsize=(12,7))

x = np.arange(0,1,0.01)
y = np.random.rand(x.shape[0])

ax[0].plot(x,y, color='gray', linestyle=':') 
"""
원래 Data 전체에 대해 그래프를 그림
아래 출력값을 확인하면 알겠지만 너무 변화가 많다. 
나는 Trend에 대해서 알고 싶기 때문에 Moving Average 방법을 활용해 데이터를 
전처리하고, 실 Data보다는 Trend에 집중하려 한다
"""

z = pd.DataFrame(y)            
# rolling을 쓰기 위해서 DataFrame으로 변환
z = z.rolling(window=10).mean()

ax[1].plot(z.index, z, color='blue', linestyle=':')
"""
중요한 점은, 원래 Data를 rolling(Moving Average)하면 x축의 값도 바뀐다는 것이다
위에서 볼 수 있듯, 앞쪽에 존재하는 Data들이 없어지기 때문이다
따라서, z.index를 x축으로 활용하여 Line Plot을 그려야 한다
"""

plt.show()
# 오른쪽 그래프가 그나마 Trend 파악이 쉬움을 알 수 있다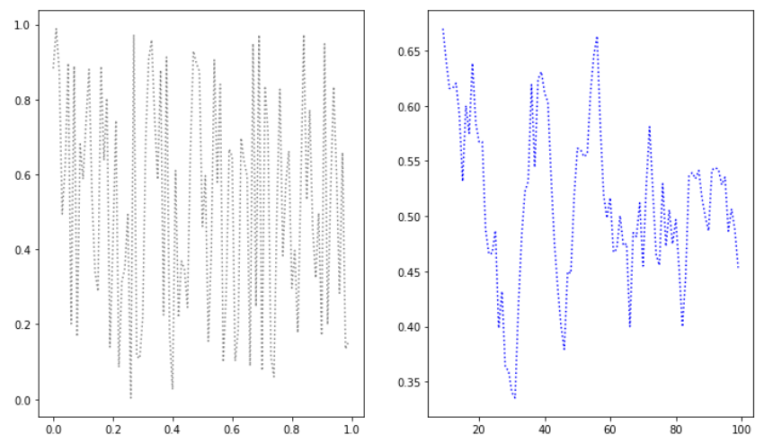

Scatter Plot

Scatter Plot이란?

점을 활용하여 두 Feature 간 관계를 알기 위해 사용하는 차트
색, 모양, 크기를 설정할 수 있음
목적 : 상관 관계 확인(양의 상관관계, 음의 상관관계, 없음)
- 군집 : 어떤 식으로 데이터가 묶여 있는가
- 군집 2개 간 값이 얼마나 차이 나는가
- 군집과 떨어져 있는 이상치 데이터 선택
Scatter Plot 정확히 그리기
- Overplotting
  - 투명도 조정
  - 지터링(jitering) : 겹치는 위치 데이터를 볼 수 있도록 점의 위치를 살짝 변경
  - 2차원 Histogram 활용
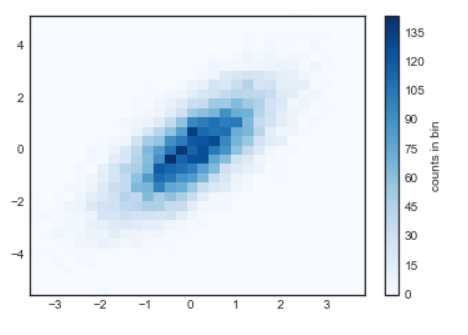
  - Contour plot : 분포를 등고선을 활용하여 표현
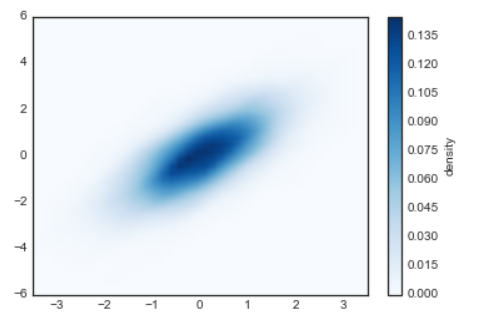
  - 그림에 대한 코드 출처 :https://jakevdp.github.io/PythonDataScienceHandbook/04.05-histograms-and-binnings.html
- 색(연속은 Gradient, 이산은 개별 색상으로 표현)
- Marker(구별이 힘들고 크기가 고르지 않음)
- 크기 : 구별하기는 쉽지만 오용하기 쉬움
  - 관계보다는 각 점간 비율에 초점을 둘 때 좋음
- 버블 차트(Bubble Chart) : 데이터를 동그란 버블로 표현하는데, 버블의 크기가 데이터의 크기(양이나 수치)를 의미함
  - 범주형이 포함된 관계에서는 Heatmap과 더불어 사용을 추천함
  - SWOT 분석(비즈니스에 사용되는 분석법)에 사용됨
인과 관계와 상관 관계를 표시하기 좋음
- 인과 관계 : 사전 정보와 함께 가정으로 제시해야 함
- 인과 관계 : A가 B에 대한 "이유가 됨"
  상관 관계 : A와 B 사건 사이에 관계가 있음
- 인과 : 비가 내리면 땅이 젖는다, 상관 : 땅이 젖었으니, 비가 왔을 확률이 높다
  - 비가 오면 물 "때문에" 땅이 젖음. 하지만 땅이 젖은 것 자체는 비가 왔다고 확신할 근거는 되지 않음
추세선 : 상관 관계를 표현할 때 활용하면 좋음 ⇒ 단, 2개 이상 활용은 지양
Grid 사용은 지양

코드로 보는 Scatter Plot

Scatter Plot 그리기

for i in range(0, 7):
    plt.scatter(0.2*i, 0, color=colors[i], s=50000, zorder=i)
# 빨간색이 가장 마지막에 그려진 scatter plot. zorder 값이 가장 크기 때문에 
# 가장 앞에 존재

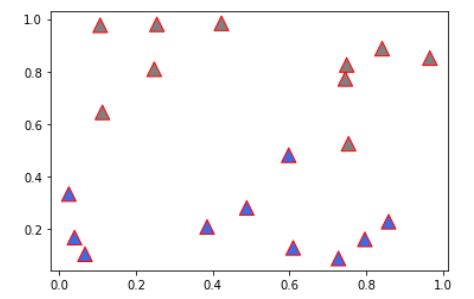
Scatter Plot Parameter
- marker : Scatter Point 모양
  - ^(삼각형), o(원), *(별) 등
- linewidth : Poinrt "테두리" 너비
- edgecolor : Point "테두리" 색깔
- color : Point 색깔
  - if 문을 활용하여 여러 개 색을 지정해 줄 수 있음
- s : Point 크기(Size)

x = np.random.rand(20)
y = np.random.rand(20)

ax.scatter(x,y,
          marker='^',
          linewidth = 1,
          edgecolor = 'r',
          color = ['royalblue' if yy <= y.mean() else 'gray' for yy in y]
          , s = 150)
# y 값이 평균보다 높으면 gray, 낮으면 royalblue로 칠했다