-
Q. 중심극한정리가 뭐냐?
A. 모집단이 평균이 뮤이고 표준편차가 세타인 임의의 분포를 이룰때 모집단의 크기가 충분히 클때 표본평균은 평균이 뮤이고 표준편차는 세타분해루트엔인 정규분포를 이룬다는 정리입니다. -
Q. 중심극한정리가 왜 필요한지 설명해봐라.
A. 중심극한정리를 통해 표본평균들의 평균과 표준편차를 구해 모집단의 평균과 표준편차를 구할 수 있는 수학적 확률적 근거가 제시가 됩니다. 또한 그 표본평균들이 모집단의 분포와는 관계없이 정규분포를 이루기 때문에 정규분포와 관련된 이론들을 적용할 수 있다.
인공지능 통계에 대해 다루기 위해 먼저 베이즈 정리를 정리한 후 이번에는 중심극한정리를 제대로 정의를 알아보기로 했다... 아마 내일은 큰수의법칙 하고나서 t test, f test, p value 등을 정리하면 될 것 같다.
사실 이 블로그를 시작한 이유에도 중심극한정리가 매우 큰 부분을 작용하는데... 카이스트 인공지능대학원 면접 보는데 중심극한정리, 큰수의법칙, p value 이렇게 3개를 순서대로 묻는데 약간 '아는듯 모르는듯' '대답은 하지만 뭔가 확실하게 알지는 않는' 대답을 했다. (인공지능 딥러닝 머신러닝은 그렇게 빡세개 공부했는데 하나도 안 물으시더라...ㅠㅠ) 사실 통계의 기본이 되는 지식들이라는 것은 아는데 제대로 대답을 못했다는 거에 내 스스로도 놀랐다. 그래서 제대로 정리하고 외우려고 이렇게 글을 썼다.
중심극한정리 Central Limit Theorem
정의 (외우자)
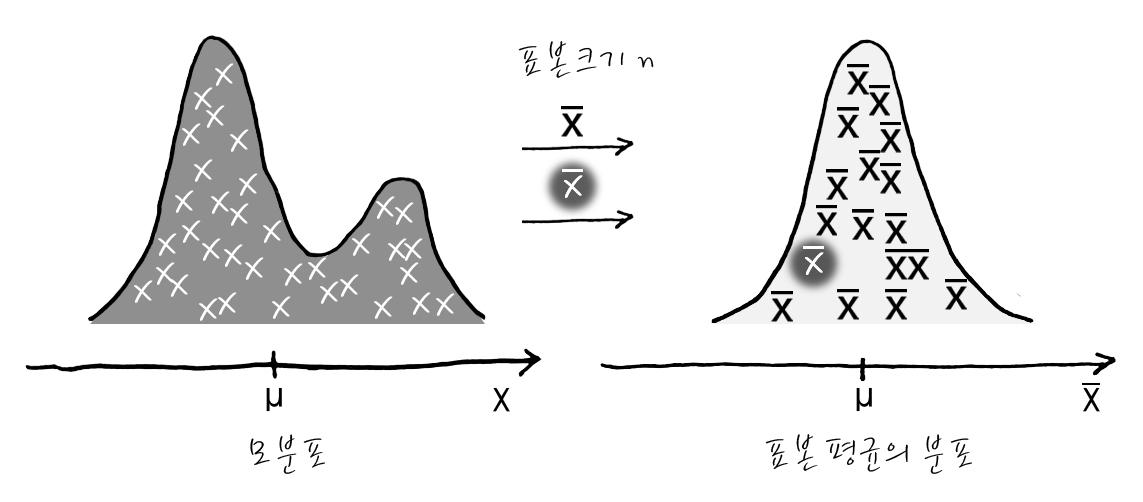
'모집단의 평균이 뮤이고 표준편차가 세타인 임의의 분포를 이룬다고 할 때, 이 모집단으로부터 추출된 표본의 크기 엔이 충분히 크면 표본평균 들은 평균이 뮤이고 표준편차는 세타분해루트엔인 정규분포 에 접근한다'
키워드는
- 모집단은 평균이 뮤이고 표준편차가 세타인 임의의 분포
- 표본의 크기가 충분히 크다
- 표본평균 들의 평균이 뮤이고 표준편차가 세타분해루트엔
- 인 정규분포에 접근한다
여기서 무조건 기억해야할 것은 중심극한정리는 '표본' 가지고 이야기하는 것이 아니라 '표본평균' 을 가지고 이야기 한다는 것이다.
표본평균을 예시로 들어 설명하자면
현재 가지고 있는 표본이 100개이면 여기서 40개를 무작위로 80번 뽑는다. 여기서 80번 뽑을때마다 40개의 값에 대한 평균이 있는데, 이들을 표본평균이라고 한다. 다른 말로, 100개 전부의 평균이 아니라 80번 뽑아 생긴 80개의 평균값들을 다룬 것이 표본평균이다.
위의 80개의 값들이 중심극한정리에서 얘기하는 표본평균이고 이 값들이 평균이 뮤이고 표준편차가 세타분해루트엔 인 정규분포를 이루는 것이다. 일단 평균과는 무조건 다른 것이다. 구별할 줄 알아야 한다.
중심극한정리가 중요한 이유 역시 알아야한다.
중심극한정리는 표본평균들을 통해 (표본이 아니라) 모집단의 뮤와 세타를 추정할 수 있다. 즉, 그 관계를 증명함으로써 수집한 표본의 통계량을 이용해 모집단의 모수를 추정할 수 있는 확률적 수학적 근거를 제시했다는 점에서 중요하다. 또한 중심극한정리를 통해 표본평균들이 정규분포를 이룬다는 것이 보여기지 때문에 정규분포와 관련된 이론들을 이용할 수 있다.
중심극한정리와 자주 물어보는 큰수의법칙에 대해서는 다음 글에 정리해야겠다.
첨부된 그림은 친절한 데이터사이언티스트 되기 강좌 https://recipesds.tistory.com 에서 발췌된 그림으로 출처를 밝힘으로써 자유롭게 사용할 수 있다고 명시하고 있습니다.