Batch Normalization (2015)

iissaacc·2021년 7월 19일

paper reading

목록 보기

4/20

updated Jul.21.21: 업데이트 전에는 그래프에 노이즈가 많았다. 혹시 학습데이터가 부족해서 그런가 해서 학습데이터를 늘려서 진행해봤더니 노이즈가 줄어들고 ICS를 관찰할 수 있었다.

Prologue

줄여서 batch norm, 더 간단하게는 bn이라고도 부른다. 이 연구에서 parameter를 업데이트 하면서 layer의 데이터 분포가 바뀌는 현상을 Internal Covariate Shift(ICS)라고 정의했다.

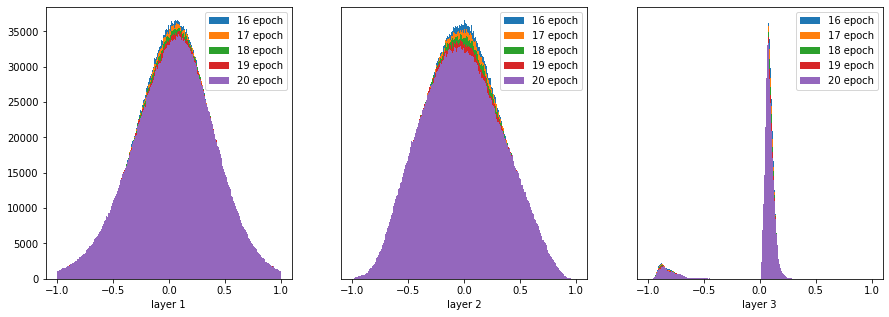
분포가 조금씩 달라지는게 보이긴 하다. layer 2를 따로 떼서 보면 이렇게 생겼다.

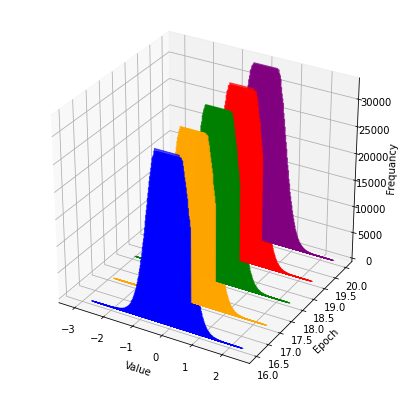
20 epoch에서 입력데이터의 분포가 갑자기 달라졌다.

What was authors try to accomplish?

이 연구에서는 ICS를 줄이는 방법을 고민했다. 구체적으로 ICS때문에 모델이 작은 변화에도 민감하게 반응한다고 생각했다. 학습률을 낮게 정하고 가중치의 초기값을 신경써야 하는 근거라고 봤는데 논문에서는 그냥 'careful'이라고 표현하고 있지만 웬지 실험을 많이 해야 한다로 읽혔다. 이 문제를 BN layer가 해결했음은 물론이고 그동안 자주 써오던 Dropout layer의 의존성을 조금 덜어낼 수도 있다.

What were key elements of the approach?

Whitening

연구자들은 원래 각 레이어에 입력되는 데이터분포를 whitening하는 것이었다. whitenning하는데는 문제점이 2가지가 있었다.

공분산 계산이 비효율적이고
억지로 쓴다고 하더라도 optimizer를 적용하기 어렵다.

Normalization

개인적으로 영상데이터를 whitening하는 게 학습에 도움이 되는지는 잘 모르겠다. 어쨌든 이런 이유들로 간단히 입력값 $x$ 를 평균이 0, 분산이 1인 분포인 $\hat{x}$ 으로 바꿔서 레이어에 입력하기로 했다. 단, 입력값이 $k$ 차원일 때 각 차원별로 normalize해야 한다.

\hat{x}^{(k)}=\frac{x^{(k)}-\mu^{(k)}}{\sigma^{(k)}}

그렇지만 sigmoid와 tanh는 0 근처에서 $f(x)=ax$ 에 가까운 모양이라서 activation function이 가지는 특성을 잃어버리는 문제가 있다.

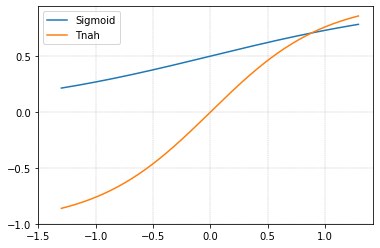
그래서 평균과 분산을 조금씩 조절하고자 $y=\gamma\hat{x} + \beta$ 로 바꿔서 $\gamma$ 와 $\beta$ 를 학습하기로 한다.

Backprop of batch norm

앞서 $\gamma$ 와 $\beta$ 를 학습한다고 했는데 $x \longrightarrow E(x) \longrightarrow \sigma^2(x) \longrightarrow \hat{x} \longrightarrow BN=\gamma\hat{x}+\beta$ 에서 우리가 필요한 미분값은 5가지다.

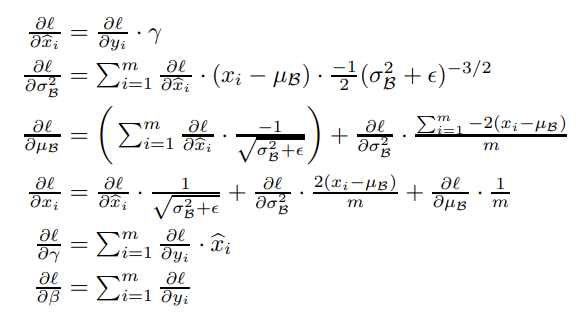
Caution

Batch size

표본평균은 표본의 크기가 커질수록 모평균과 비슷해지므로 batch size가 낮으면 효과를 볼 수 없다.

Statistics

Dropout layer처럼 학습할 때와 추론할 때가 조금 다르다. BN layer는 추론할 때 전체 학습 세트의 평균과 분산을 이용한다. 다만 우리가 학습을 통해 모델이 갖고있는 평균과 분산은 엄밀히 말하면 표본분산이므로 표본으로부터 모평균, 모분산을 추정하는 점화식에 따라 $\sigma^2(x_n)$ 에다가 $m\over(m-1)$ 을 곱해야해서 학습과 추론이 좀 다를 수 있다.

Why is it working?

gradient가 크면 weight initialization에서 봤듯이 gradient vanishing/exploding이 일어나거나 local minima에 갇힌다. BN layer는 ICS를 줄여줘서 모델이 변화에 덜 민감하게 만들어준다고 주장한다. 이후 실험에서 학습률을 높이고 dropout layer처럼 계산이 많이 드는 요소를 줄여서 학습시간을 효과적으로 줄였다고 하면서 주장을 뒷받침한다.