Derivative of conv layer

iissaacc·2021년 12월 22일
BackpropagationCNN
0

deep learning

목록 보기
11/12

Prologue

MLP에서 backward pass를 리뷰한 것을 활용해서 conv lyaer가 내부적으로는 어떻게 돌아가는지 알아보면 좋을 것 같다는 생각에서 시작했다. 레쓰고.

Forward pass

Conv layer에서는 기본적으로 이미지를 kenel의 크기만큼 submatrix로 쪼개서(물론 padding, strides를 고려해서) frobenius product한다. 이전 글에서도 짚었듯이 크기가 같은 행렬 A, BA,\ B가 있을 때 두 matrix를 frobenius product연산한다고 하면 ⟨A,B⟩F=∑i∑jai,j⋅bi,j\langle A,B\rangle_F=\sum_i\sum_j a_{i,j}\cdot b_{i,j}이렇게 표현한다. 예를 들어 이미지 X∈R3×3X\in\mathbb{R}^{3\times3}와, kernel W∈R2×2W\in\mathbb{R}^{2\times2}가 주어지고 padding=0, strides=1 일 때 XX를 4가지 submatrix로 쪼갤 수 있다.

X=[X11X12X21X22]=[[x11x12x21x22][x12x13x22x23][x21x22x31x32][x22x23x32x33]]X= \begin{bmatrix} X_{11}&X_{12}\\ \\ X_{21}&X_{22} \end{bmatrix}= \begin{bmatrix} \begin{bmatrix}x_{11} & x_{12} \\ x_{21} & x_{22} \end{bmatrix}& \begin{bmatrix}x_{12} & x_{13} \\ x_{22} & x_{23} \end{bmatrix}\\ \\ \begin{bmatrix}x_{21} & x_{22} \\ x_{31} & x_{32} \end{bmatrix}& \begin{bmatrix}x_{22} & x_{23} \\ x_{32} & x_{33} \end{bmatrix} \end{bmatrix}

이 때, 각 4개의 submatrix와 WW를 frobenius product하면 수식으로 이렇게 표현한다.

X⊛W=[⟨W,X11⟩F⟨W,X12⟩F⟨W,X21⟩F⟨W,X22⟩F]X\circledast W= \begin{bmatrix} \langle W,X_{11}\rangle_F & \langle W,X_{12}\rangle_F\\ \\ \langle W,X_{21}\rangle_F & \langle W,X_{22}\rangle_F \end{bmatrix}

정확히 conv layer에서 일어나는 연산과 일치한다. 편의를 위해 이 matrix는 FF라고 이름 붙이고
F=[f11f12f21f22]F= \begin{bmatrix} \text{f}_{11} & \text{f}_{12} \\ \text{f}_{21} & \text{f}_{22} \end{bmatrix}이렇게 정의하자. 목표는 conv layer의 backpropagation이니까 일단 FF를 다 풀어서 계산해놓는다.

f11=x11w11+x12w12+x21w21+x22w22f12=x12w11+x13w12+x22w21+x23w22f21=x21w11+x22w12+x31w21+x32w22f22=x22w11+x23w12+x32w21+x33w22\text{f}_{11}=x_{11}w_{11}+x_{12}w_{12}+x_{21}w_{21}+x_{22}w_{22}\\ \text{f}_{12}=x_{12}w_{11}+x_{13}w_{12}+x_{22}w_{21}+x_{23}w_{22}\\ \text{f}_{21}=x_{21}w_{11}+x_{22}w_{12}+x_{31}w_{21}+x_{32}w_{22}\\ \text{f}_{22}=x_{22}w_{11}+x_{23}w_{12}+x_{32}w_{21}+x_{33}w_{22}\\

준비는 끝났다. 이제 계산할 일만 남았다.

Backward pass

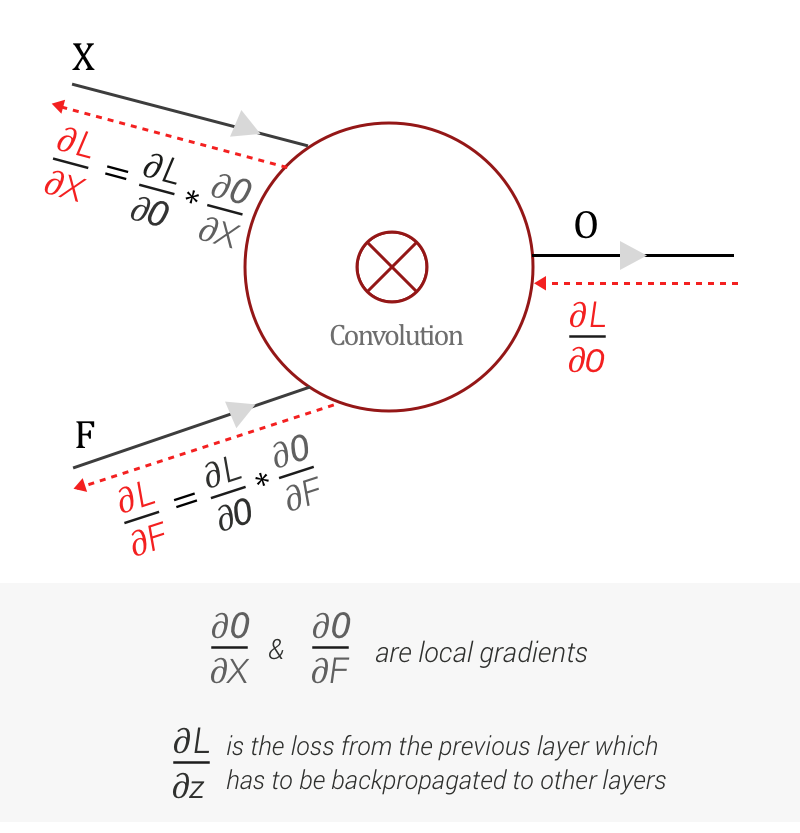
MLP에서 일어나는 Backward pass와 똑같이 chain rule을 활용해서 계산하면 된다. 다만 차이는 scaler나 vector가 아니라 matrix로 연산해야 한다는 점이다.

Prep

Chain rule을 활용하기 위해 ∂L∂F, ∂F∂X, ∂F∂W\frac{\partial{L}}{\partial{F}}_,\ \frac{\partial{F}}{\partial{X}}_,\ \frac{\partial{F}}{\partial{W}} 세 가지를 먼저 계산해줄거다.

∂L∂F=[∂L∂f11∂L∂f12∂L∂f21∂L∂f22]\frac{\partial{L}}{\partial{F}}= \begin{bmatrix}\frac{\partial{L}}{\partial{\text{f}_{11}}}& \frac{\partial{L}}{\partial{\text{f}_{12}}}\\ \\ \frac{\partial{L}}{\partial{\text{f}_{21}}}& \frac{\partial{L}}{\partial{\text{f}_{22}}} \end{bmatrix}

∂F∂W=[∂F∂w11∂F∂w12∂F∂w21∂F∂w22]=[[x11x12x21x22][x12x13x22x23][x21x22x31x32][x22x23x32x33]]\frac{\partial{F}}{\partial{W}}= \begin{bmatrix} \frac{\partial{F}}{\partial{w_{11}}}& \frac{\partial{F}}{\partial{w_{12}}}\\ \\ \frac{\partial{F}}{\partial{w_{21}}}& \frac{\partial{F}}{\partial{w_{22}}} \end{bmatrix}= \begin{bmatrix} \begin{bmatrix} x_{11}&x_{12}\\x_{21}&x_{22} \end{bmatrix}& \begin{bmatrix} x_{12}&x_{13}\\x_{22}&x_{23} \end{bmatrix}\\ \\ \begin{bmatrix} x_{21}&x_{22}\\x_{31}&x_{32} \end{bmatrix}& \begin{bmatrix} x_{22}&x_{23}\\x_{32}&x_{33} \end{bmatrix} \end{bmatrix}

∂F∂X=[∂F∂x11∂F∂x12∂F∂x13∂F∂x21∂F∂x22∂F∂x23∂F∂x31∂F∂x32∂F∂x33]=[[w11000][w12w1100][0w1200][w210w110][w22w21w12w11][0w220w12][00w210][00w22w21][000w22]]\frac{\partial{F}}{\partial{X}}= \begin{bmatrix} \frac{\partial{F}}{\partial{x_{11}}}& \frac{\partial{F}}{\partial{x_{12}}}& \frac{\partial{F}}{\partial{x_{13}}}\\ \\ \frac{\partial{F}}{\partial{x_{21}}}& \frac{\partial{F}}{\partial{x_{22}}}& \frac{\partial{F}}{\partial{x_{23}}}\\ \\ \frac{\partial{F}}{\partial{x_{31}}}& \frac{\partial{F}}{\partial{x_{32}}}& \frac{\partial{F}}{\partial{x_{33}}} \end{bmatrix}= \begin{bmatrix} \begin{bmatrix}w_{11}&0\\0&0\end{bmatrix}& \begin{bmatrix}w_{12}&w_{11}\\0&0\end{bmatrix}& \begin{bmatrix}0&w_{12}\\0&0\end{bmatrix}\\ \\ \begin{bmatrix}w_{21}&0\\w_{11}&0\end{bmatrix}& \begin{bmatrix}w_{22}&w_{21}\\w_{12}&w_{11}\end{bmatrix}& \begin{bmatrix}0&w_{22}\\0&w_{12}\end{bmatrix}\\ \\ \begin{bmatrix}0&0\\w_{21}&0\end{bmatrix}& \begin{bmatrix}0&0\\w_{22}&w_{21}\end{bmatrix}& \begin{bmatrix}0&0\\0&w_{22}\end{bmatrix} \end{bmatrix}

Chain rule

전제는 forward pass 때 convolution했으므로 packward pass때도 convolution한다.

dL/dW

따지고 보면 ∂F∂W=[X11X12X21X22]\frac{\partial{F}}{\partial{W}}= \begin{bmatrix} X_{11}&X_{12}\\ X_{21}&X_{22} \end{bmatrix}가 성립한다. 생격을 좀더 이어가서 ∂L∂W\frac{\partial{L}}{\partial{W}}는 XX의 submatrix와 ∂L∂F\frac{\partial{L}}{\partial{F}}를 frobenius product하는 것과 같은 샘이 된다. 그러니까

∂F∂W⋅∂L∂F=[⟨∂L∂F,X11⟩F⟨∂L∂F,X12⟩F⟨∂L∂F,X21⟩F⟨∂L∂F,X22⟩F]\frac{\partial{F}}{\partial{W}}\cdot\frac{\partial{L}}{\partial{F}}= \begin{bmatrix} \langle \frac{\partial{L}}{\partial{F}},X_{11}\rangle_F & \langle \frac{\partial{L}}{\partial{F}},X_{12}\rangle_F\\ \\ \langle \frac{\partial{L}}{\partial{F}},X_{21}\rangle_F & \langle \frac{\partial{L}}{\partial{F}},X_{22}\rangle_F \end{bmatrix}

이 말과도 성립한다.

dL/dX

이것도 앞서 ∂L∂W\frac{\partial{L}}{\partial{W}}를 연산한 것처럼 convolution을 활용한다.

∂F∂X⋅∂L∂F=[⟨∂L∂F,∂F∂x11⟩F⟨∂L∂F,∂F∂x12⟩F⟨∂L∂F,∂F∂x13⟩F⟨∂L∂F,∂F∂x21⟩F⟨∂L∂F,∂F∂x22⟩F⟨∂L∂F,∂F∂x23⟩F⟨∂L∂F,∂F∂x31⟩F⟨∂L∂F,∂F∂x32⟩F⟨∂L∂F,∂F∂x33⟩F]\frac{\partial{F}}{\partial{X}}\cdot\frac{\partial{L}}{\partial{F}}= \begin{bmatrix} \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{11}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{12}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{13}}}\rangle_F\\ \\ \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{21}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{22}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{23}}}\rangle_F\\ \\ \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{31}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{32}}}\rangle_F& \langle\frac{\partial{L}}{\partial{F}},\frac{\partial{F}}{\partial{x_{33}}}\rangle_F\\ \end{bmatrix}

이 문제는 ∂L∂W\frac{\partial{L}}{\partial{W}}에서 그랬듯 기존 matrix를 바로 활용하기는 어려워보인다. 그럴 땐 일단 계산해보면 된다.

[∂L∂f11w11∂L∂f11w12+∂L∂f12w11∂L∂f12w12∂L∂f11w21+∂L∂f21w11∂L∂f11w22+∂L∂f12w21+∂L∂f21w12+∂L∂f22w11∂L∂f12w22+∂L∂f22w12∂L∂f21w21∂L∂f21w22+∂L∂f22w21∂L∂f22w22]\begin{bmatrix} \frac{\partial{L}}{\partial{\text{f}_{11}}}w_{11}& \frac{\partial{L}}{\partial{\text{f}_{11}}}w_{12}+ \frac{\partial{L}}{\partial{\text{f}_{12}}}w_{11}& \frac{\partial{L}}{\partial{\text{f}_{12}}}w_{12}\\ \\ \frac{\partial{L}}{\partial{\text{f}_{11}}}w_{21}+ \frac{\partial{L}}{\partial{\text{f}_{21}}}w_{11}& \frac{\partial{L}}{\partial{\text{f}_{11}}}w_{22}+ \frac{\partial{L}}{\partial{\text{f}_{12}}}w_{21}+ \frac{\partial{L}}{\partial{\text{f}_{21}}}w_{12}+ \frac{\partial{L}}{\partial{\text{f}_{22}}}w_{11}& \frac{\partial{L}}{\partial{\text{f}_{12}}}w_{22}+ \frac{\partial{L}}{\partial{\text{f}_{22}}}w_{12}\\ \\ \frac{\partial{L}}{\partial{\text{f}_{21}}}w_{21}& \frac{\partial{L}}{\partial{\text{f}_{21}}}w_{22}+ \frac{\partial{L}}{\partial{\text{f}_{22}}}w_{21}& \frac{\partial{L}}{\partial{\text{f}_{22}}}w_{22} \end{bmatrix}

어렵지는 않지만 복잡하다

Epilogue

문제를 좀더 직관적으로 보려면 시각적으로 생각할 필요가 있다. ∂F∂X\frac{\partial{F}}{\partial{X}}를 계산하면서 정중앙 matrix가 기존의 WW를 180도 뒤집어 놓은 모양이라는 점을 눈치챘을 것이다. 이 점을 이용한다. 그 전에 ∂L∂F\frac{\partial{L}}{\partial{F}}에 1만큼 padding하고 submatrix 9개로 나눠준다.

pad1(∂L∂F)=[[000∂L∂f11][00∂L∂f11∂L∂f12][00∂L∂f120][0∂L∂f110∂L∂f21][∂L∂f11∂L∂f12∂L∂f21∂L∂f22][∂L∂f120∂L∂f220][0∂L∂f2100][∂L∂f21∂L∂f2200][∂L∂f22000]]rot180(W)=[w22w21w12w11]pad_{1}(\frac{\partial{L}}{\partial{F}})= \begin{bmatrix} \begin{bmatrix} 0&0\\ 0&\frac{\partial{L}}{\partial{\text{f}_{11}}} \end{bmatrix}& \begin{bmatrix} 0&0\\ \frac{\partial{L}}{\partial{\text{f}_{11}}}& \frac{\partial{L}}{\partial{\text{f}_{12}}} \end{bmatrix}& \begin{bmatrix} 0&0\\ \frac{\partial{L}}{\partial{\text{f}_{12}}}&0 \end{bmatrix}\\ \\ \begin{bmatrix} 0&\frac{\partial{L}}{\partial{\text{f}_{11}}}\\ 0&\frac{\partial{L}}{\partial{\text{f}_{21}}} \end{bmatrix}& \begin{bmatrix} \frac{\partial{L}}{\partial{\text{f}_{11}}}& \frac{\partial{L}}{\partial{\text{f}_{12}}}\\ \frac{\partial{L}}{\partial{\text{f}_{21}}}& \frac{\partial{L}}{\partial{\text{f}_{22}}} \end{bmatrix}& \begin{bmatrix} \frac{\partial{L}}{\partial{\text{f}_{12}}}&0\\ \frac{\partial{L}}{\partial{\text{f}_{22}}}&0 \end{bmatrix}\\ \\ \begin{bmatrix} 0&\frac{\partial{L}}{\partial{\text{f}_{21}}}\\ 0&0 \end{bmatrix}& \begin{bmatrix} \frac{\partial{L}}{\partial{\text{f}_{21}}}& \frac{\partial{L}}{\partial{\text{f}_{22}}}\\ 0&0 \end{bmatrix}& \begin{bmatrix} \frac{\partial{L}}{\partial{\text{f}_{22}}}&0\\ 0&0 \end{bmatrix}\\ \end{bmatrix}\quad rot_{180}(W)= \begin{bmatrix} w_{22}&w_{21}\\ w_{12}&w_{11} \end{bmatrix}

pad1(∂L∂F)pad_1(\frac{\partial{L}}{\partial{F}})의 submatrix 9개와 rot180(W)rot_{180}(W)를 각각 frobenius product하면 ∂F∂W\frac{\partial{F}}{\partial{W}}를 계산하는 과정을 생략하고 구할 수 있다.

profile
iissaacc
이전 포스트

Swish function

다음 포스트

TensorRT 101

0개의 댓글