Prologue
어떤 연구에서는 Swish, 또 다른 연구에서는 SiLU로 불린다. activation function 연구는 활발하게 이루어지지만 어떤 과제에서 잘 되는 함수가 다른 과제에서는 잘 안 되는 게 많아서 자주 쓰이는 건 한정적이다. Swish는 어디선가 잘된다고 스쳐서 들어본 김에 그래프를 본 적은 있지만 점화식도 처음 보고 써 본적은 더욱 없다.
Formula
Sigmoid에 입력값을 한 번 더 곱해주는 모양이지만 ReLU와 비슷하게 생겨서 특성도 ReLU와 상당히 비슷할 것 같다.
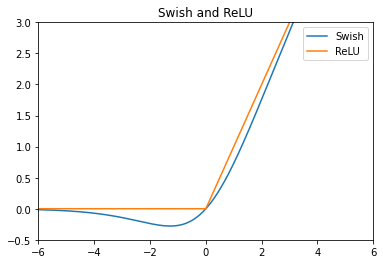
Derivative
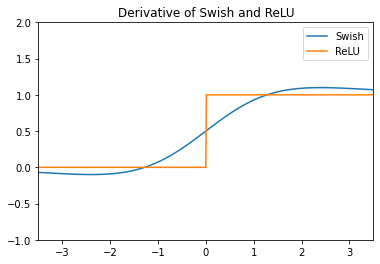
Andrej Karpathy가 짚었듯[2] 처음 보는 layer는 미분을 해봐야 마땅하다.
Properties
연구에서는 ReLU를 사용한 모델에서 activation function만 Swish로 바꾼 모든 실험에서 Swish가 ReLU를 압도한다고 밝혔다. 그 이유에 대해서 정확하지는 않지만 아래 4가지 때문이 아닐까하고 추측하고 있다.
- Unbounded above where
- Bounded below where
- Non monotonicity
- Smooth figure
Unbounded above
Sigmoid와 Tanh는 각각 , 를 범위로하지만 ReLU의 범위는 이다. 이 점이 gradient vanish를 막아준다. 이 점이 ReLU의 전성기를 가져왔고 Swich를 비롯해서 최근에 나오는 activation function이 이 특성을 여전히 이어받고 있다.
Bounded below
이런 특성은 많은 activation function이 가지고 있다. 너무 큰 음수값은 으로 내보내서 일종의 강한 규제를 거는 효과가 있다. 그렇지만 ReLU에서는 음수값에 대해서는 무조건 을 내보내므로 dying ReLU에 직면한다는 점이 단점으로 작용해서 Leaky ReLU나 PReLU가 파생형으로 나왔다. Swish는 어느 정도 작은 음수값에 대해서 허용하고 있다. 이 점은 non monotonicity와도 이어진다.
Non monotonicity
Swish는 앞서 언급한 것처럼 약간의 음수를 허용하고 있고 심지어 양수부분은 직선 그래프가 아니다. ReLU와 비슷하게 생겼지만 오히려 표현력이 좋다. 미분그래프에서 0 근처를 보면 ReLU와의 차이점이 확연히 보인다. 전에 Step에 비해 Sigmoid가 가진 장점을 논의했듯이 gradient로 작은 음수가 전해지더라도 온전히 이전 layer로 전할 수 있어서 학습이 잘 된다.
Smooth figure
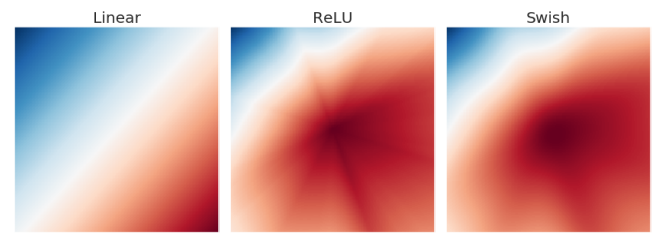
6개 layer를 가진 임의의 신경망을 학습해서 출력 layer의 activation map이다. ReLU에서 별모양이 눈에 띄는데 activation map 상에서 갑작스러운 변화를 의미한다. 이건 작은 변화에도 민감하게 반응하게 만들어서 모델이 학습을 어렵게 하는 원인이라고 다른 연구에서 지목하기도 한다. Swish처럼 경계가 흐릿하면 ReLU와는 반대로 작은 변화에는 작게, 큰 변화에는 크게 반응하게 해서 optimizer가 제대로 minima를 찾아가게 한다.
Epilogue
Variants: Swish-
EfficientNet에서 를 1로 하는 swish-1을 쓴다. 최적의 를 찾아야 하는 과제가 하나 더 주어진 셈이다. 이 점을 참고하면
- ,
이 두 가지를 짐작할 수 있다. 만약 도 parameter로 넣으면 학습 중에 Linear, Swish, ReLU사이를 왔다 갔다하면서 layer차원에서 최적의 activation function을 찾아간다는 말이기도 하다. 와!
https://pumpyoursound.com/u/user/1519313
https://sfx.thelazy.net/users/u/chinabamboo/
https://www.fantasyplanet.cz/diskuzni-fora/users/chinabamboo/
https://www.gta5-mods.com/users/chinabamboo
https://www.pintradingdb.com/forum/member.php?action=profile&uid=108220
https://www.wvhired.com/profiles/7038403-china-bamboo
https://all4.vip/p/page/view-persons-profile?id=87767
https://careers.gita.org/profiles/7038388-china-bamboo
https://www.fundable.com/china-bamboo
https://varecha.pravda.sk/profil/chinabamboo/o-mne/
https://www.forum-joyingauto.com/member.php?action=profile&uid=48040
https://www.mikocon.com/home.php?mod=space&uid=256736
https://scrapbox.io/chinabamboo/chinabamboo
https://slatestarcodex.com/author/chinabamboo/
https://hanson.net/users/chinabamboo
http://www.fanart-central.net/user/chinabamboo/
https://www.rwaq.org/users/bothbest-20250813145515
https://www.zubersoft.com/mobilesheets/forum/user-89124.html
https://www.niftygateway.com/@chinabamboo/
https://protospielsouth.com/user/77682
https://whyp.it/users/100591/chinabamboo
https://bulkwp.com/support-forums/users/chinabamboo/
https://spinninrecords.com/profile/chinabamboo
https://fyers.in/community/member/MAGfDcP7tF
https://velog.io/@chinabamboo/posts
https://robertsspaceindustries.com/en/citizens/chinabamboo
https://unityroom.com/users/chinabamboo
https://www.aseeralkotb.com/ar/profiles/china-bamboo-bfc-116365576188419692513-1755394900
https://mathlog.info/users/Y7CG8ma0cAeikQnPJW0IDMbf8EW2
https://mathlog.info/articles/RW0eKy1Cls8auLMkkODN