EfficientNet

iissaacc·2021년 10월 12일

Compound scaling Computer Vision EfficientNet

paper reading

목록 보기

9/20

updated Nov.02.21: MBConv 보충
updated Nov.05.21: 모델구현(EfficientNet-B0)
TODO: Compound scaling 구현
updated Nov.24.21: Compound scaling 수정

Prologue

AlexNet 이후로 CNN은 덩치를 키우는 방식으로 정확도를 높여왔고 그 꽃이 ResNet이다. 이후의 CNN연구는 두 방향으로 갈린다.

정확도를 높인다.(Accuracy)

Model Top-1 Accuracy (%) Parameter (Mill)
SENet 82.7 145
Gpipe 84.3 557

이렇게 큰 모델을 학습하려면 모델을 여러 GPU에 나누어야 한다. 이런 점을 봤을 때도 하드웨어의 한계에 다다랐고 추가적인 정확도 향상을 위해 연산량을 줄일 수밖에 없다는 결론을 내릴 수 있다.
연산량을 줄인다.(Efficiency)
모바일 기기가 많아지만서 model compression 연구도 활발하게 진행하고 있다. 그동안 layer 수, kernel 수, kernel 타입을 일일이 바꿔가면서 수많은 실험을 했고 SqueezeNet, MobileNet, Shufflenet 같은 모델들을 찾아냈다. 모델이 가벼워졌지만 대신 정확도를 약간 희생해야 했다.

Model	Top-1 Accuracy (%)	Parameter (Mill)
SENet	82.7	145
Gpipe	84.3	557

What did authors try to accomplish?

지금까지 CNN은 다음 3가지 중 하나만 늘리는 방향으로 발전해왔다.

Depth(more layer) e.g. ResNet
Width(more kernel) e.g. MobileNet
Resolution(bigger spatial size) e.g. Gpipe

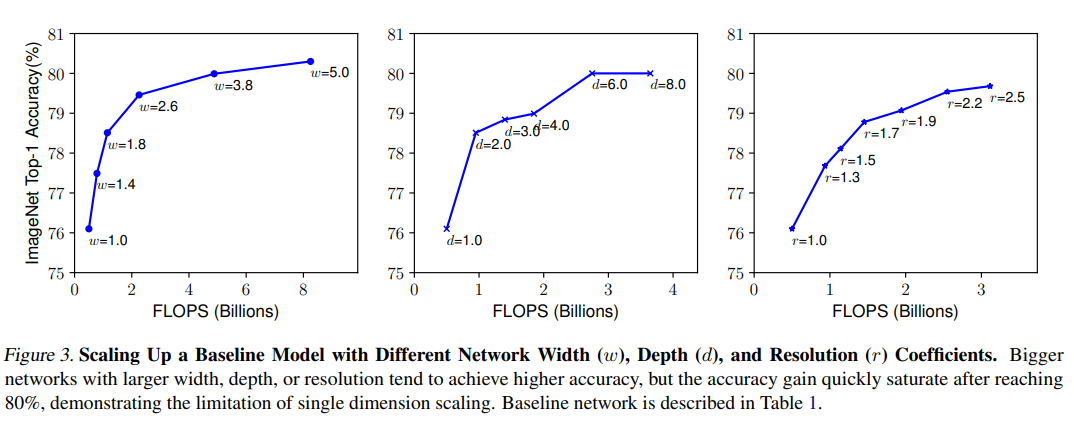
어느 한 차원만 늘리면 성능이 확실히 좋아지다가 80% 근처에서 더이상 좋아지지 않는다. ResNet에서도 152 layer 모델과 1202 layer 모델은 성능적인 차이가 거의 없다고 서술하고 있다. 연구자들은 모바일 환경에 올라가면서 정확도가 높은 모델을 만들고 싶었다. 최대한 가벼운 모델을 찾아서 기기의 성능이 허락하는 한 체계적으로 depth, width, resolution을 늘려서 정확도와 연산효율을 향상할 방법을 찾고 싶었다.

What were key elements to approach?

MnasNet

Mobie Neural Architecutre Search NETwork를 줄인 말. 그러니까 모바일이나 임베디드 환경에 적합한 CNN 구조를 찾기위한 신경망이다. 이제는 모델도 사람이 아니라 신경망이 찾는다. 🙊🙊 이전 연구에서 지적하고 있듯이 모델을 설계하는데 맨땅에 박치기하기에는 search space가 너무 넓어서 시간과 비용이 많이 든다. 이것 마저도 신경망에 맡기면 비교적 짧은 시간 안에 편향없이 정해둔 규칙에 따라 모델을 만들 수 있을 거라는 의도가 들어있다.

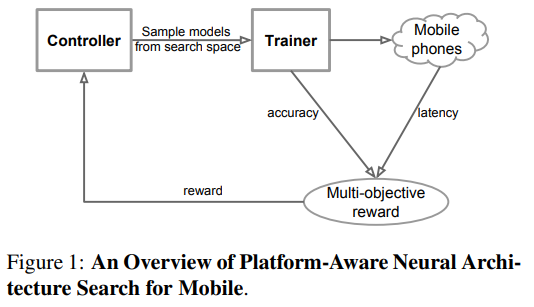
먼저 controller가 search space안에서 초기모델을 찾는다.
1에서 찾은 모델을 학습하고 평가한다.
실제로 모바일기기에 얹어서 응답시간을 측정한다.
2, 3에서 얻은 결과를 cost function에 입력한다.
4의 결과를 바탕으로 정확도가 높은 방향으로, 응답시간이 짧은 방향으로 controller에 보상한다.

이 때 controller의 큰 목적은 앞 단락에서 서술했듯이 목표 응답시간 안에서 가장 높은 정확도를 갖게하는 모델을 찾는 것이다. 보상은 아래 objective function에 따른다.

\text{maximize}_m\quad ACC(m)\times{\left[\cfrac{LAT(m)}{T}\right]}^w\\

\ \ \qquad\qquad\text{where }w\text{ is defined as: } w=\begin{cases}\alpha,\quad \text{if }LAT(m)\le T \\ \beta,\quad \text{otherwise}\end{cases}

$ACC(m),\ LAT(m),\ T$ 는 각각 controller에서 제안한 모델의 정확도, 추론 응답시간, 목표 응답시간, $w$ 는 정확도와 응답시간 사이의 trade-off를 조율하는 가중치다. EfficientNet-B0을 찾을 때는 특정 기기에서 잘 되는 모델이 아니라 범용으로 쓸 수 있는 모델을 찾고 싶다는 의도에서 직접적으로 $LAT(m)$ 을 재는 대신 $FLOPS(m)$ 을 사용하고 $w$ 는 $-0.07$ 로 했다. 크게 봤을 때 학습규칙만 주어지고 그 결과에 따라 보상이 주어진다는 측면에서 뭔가 강화학습같기도 하다. 어쨌든 이렇게 찾은 초기모델이 EfficientNet-B0.

Architecture

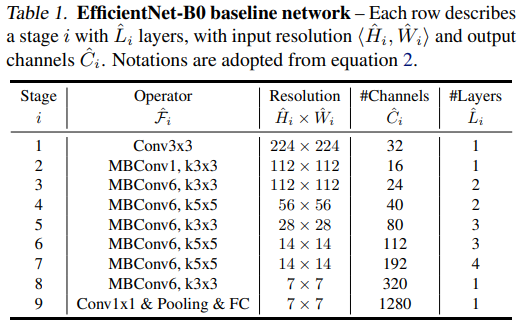
MBConv

이전 모델에는 안 보이던 layer다. MobileNetv2를 만드는 기본적인 block이고 MnasNet의 영향을 받아서 중간에 SE block이 들어있다. 기본적으로는 이렇게 생겼다.

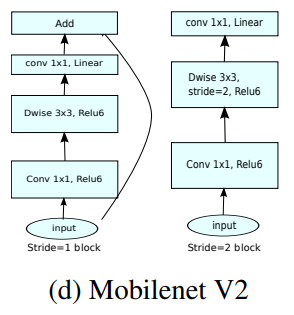
ResNet에서는 첫번째 bottleneck에서 channel을 줄였다가 두번째 bottleneck에서 원래대로 돌려놓도록 설계하고 있다. MobileNetv2에서는 ResNet과는 반대로 오히려 첫번째 bottleneck에서 expansion factor를 곱해서 channel을 늘리고 두번째 bottleneck에서 원래대로 돌려놓는다. 그래서 MobileNetv2의 모듈을 inverted residual block이라고 부른다.

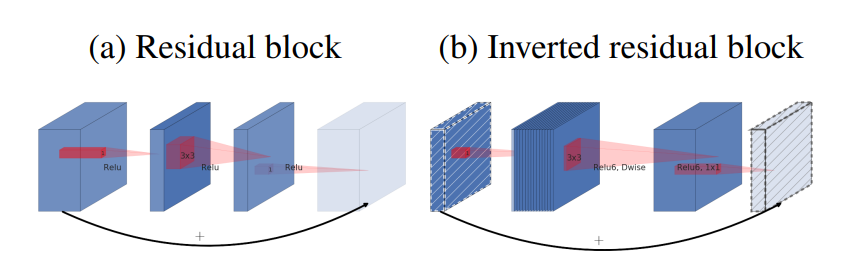
이 때 expansion factor에 따라 MBConv1 혹은 MBConv6으로 부르고 있다. MnasNet에서는 이렇게 만든 inverted residual block에다가 SE block을 더 붙여서 표현력을 키웠다.

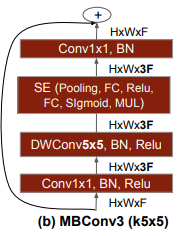
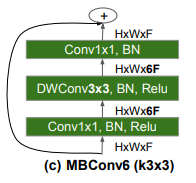
이렇게 두 가지 모델에서 사용한 block을 적절하게 섞어서 EfficientNet-B0를 만들었다. 거듭 강조하지만 사람이 아니라 신경망이 만들었다.

Compound scaling

이 연구에서 CNN을 수식으로 아래와 같이 정의했다.

\mathcal{N}=\bigodot_{i=1\dots s}{\mathcal{F}_i}^{L_i}(X_{\langle{H_i,\ W_i,\ C_i}\rangle})

$\bigodot$ 기호로 합성함수 $\mathcal{F}_n(\dots(\mathcal{F}_2(\mathcal{F}_1(X)))$ 를 간략하게 표현했다. 이 때 높이, 너비, 채널로 $H_i,\ W_i,\ C_i$ 을 가지는 입력 tensor $X$ 를 $i$ 개 stage로 나누어진 CNN에 입력하는데 각 stage는 다시 $L_i$ 개의 layer로 구성되어있다. 그러니까 ResNet은 ${\mathcal{F}_1}^{1}$ 의 입력값으로 $\langle224,\ 224,\ 3\rangle$ 크기의 이미지를 입력값으로, ${\mathcal{F}_5}^{9}$ 에서는 $\langle7,\ 7,\ 512\rangle$ 크기의 tensor를 입력값으로 받는다.

이전의 연구에서는 최적의 구조를 가지는 $\mathcal{F}$ 를 찾지만 이 연구는 모델의 구조는 가만히 놔두고 모델의 깊이 $(L_i)$ , 너비 $(C_i)$ , 입력값의 크기 $(H_i,\ W_i)$ 를 조절해서 모델의 크기를 조절한다. 그러면 kernel_size, stride, padding같은 parameter는 생략하면서 search space를 조금 좁힐 수 있지만 $L_i,\ C_i,\ H_i,\ W_i$ 를 일일이 grid search로 찾기에는 여전히 커서 함수 $\mathcal{N}$ 에 모델의 깊이, 너비, 입력값의 크기에 해당하는 가중치 $d,\ w,\ r$ 을 입력하는 함수로 문제를 좀더 단순하게 만들기로 했다.

\mathcal{N}(d,\ w,\ r)=\bigodot_{i=1\dots s}\mathcal{\hat{F}}_i^{d\cdot L_i}(X_{\langle{r\cdot \hat{H_i},\ r\cdot \hat{W_i},\ w\cdot\hat{C_i}}\rangle})

그래서 문제는 $d,\ w,\ r$ 을 조절해서 모델에 있는 모든 layer의 수, 입력값의 크기, kernel의 수를 조절할 수 있다

\text{{max}}_{d,\ w,\ r}\quad Accuracy(\mathcal{N}(d,\ w,\ r))

\quad\text{Memory}(\mathcal{N})\le\text{target memory}\\ \text{FLOPS}(\mathcal{N})\le\text{target flops}

최종적으로는 이렇게 만든 모델이 목표하는 메모리와 $FLOPS$ 를 넘어가지 않도록 한다.

\qquad\text{detph: }d=\alpha^\phi\\ \qquad\text{width: }w=\beta^\phi\\ \text{resolution: }r=\gamma^\phi\\ \qquad\qquad\quad\quad s.t.\ \alpha\cdot\beta^2\cdot\gamma^2\approx2\\ \quad\quad\qquad\qquad\qquad\qquad\alpha\ge1,\ \beta\ge1,\ \gamma\ge1

$FLOPS$ 는 cnn의 연산량이 많을수록 함께 늘어난다. 그러므로 모델의 $d,\ w,\ r$ 을 각각 2배씩 늘려줄 때 연산량과 $FLOPS$ 는 2배, 4배, 4배씩 늘어난다. 간단히 CNN의 연산량을 계산해볼 거다. 예시에서는 편의를 위해 conv layer의 stride는 1, padding은 'same'으로 한다.

$\text{Let: }t=K\cdot K\cdot C_{in}\cdot H_{out}\cdot W_{out}\cdot C_{out}\\$

$nd=t_1+t_2+\dots+t_n=nt\quad\text{where }1,\ 2, \dots,n\text{ are stage index}\\ nw=K\cdot K\cdot nC_{in}\cdot H_{out}\cdot W_{out}\cdot nC_{out}=n^2t\\ nr=K\cdot K\cdot C_{in}\cdot nH_{out}\cdot nW_{out}\cdot C_{out}=n^2t$

그래서 모델의 $FLOPS$ 는 $\alpha\cdot\beta^2\cdot\gamma^2$ 로 계산한다. $d$ 보다 $w,\ r$ 이 더 가파르게 증가하므로 $\alpha$ 의 증가량은 $n$ 이 아니라 1로 고정하는 것 같다. 다만 $\alpha,\ \beta, \gamma$ 는 위의 정의에서처럼 $\alpha\cdot\beta^2\cdot\gamma^2$ 를 $2$ 에 가까운 실수가 되도록 제한하고 $\phi$ 를 조금씩 조절하면서 $FLOPS$ 가 $2^{\phi}$ 만큼 늘어나도록 했다. 그러면 MnasNet이 찾은 EfficientNet-B0를 compound scaling하는지 알아보자.

Scaling stratagy

EfficientNet-B0는 이름에 걸맞게 $\phi$ 가 0이므로 먼저 $\phi$ 를 1로 고정하고 grid search로 $\alpha,\ \beta,\ \gamma$ 를 찾는다. 이렇게 찾은 $\alpha,\ \beta,\ \gamma$ 는 $\phi$ 를 차차 올려서 B1-B7을 만들었다. 연구에서는 EfficientNet-B0를 가장 좋은 성능을 내는 $\alpha,\ \beta,\ \gamma$ 는 각각 1.2, 1.1, 1.15였다. 물론 크게 만드는데는 여력이 있다는 조건이 따라 붙어야 한다.

Scaling EfficientNet

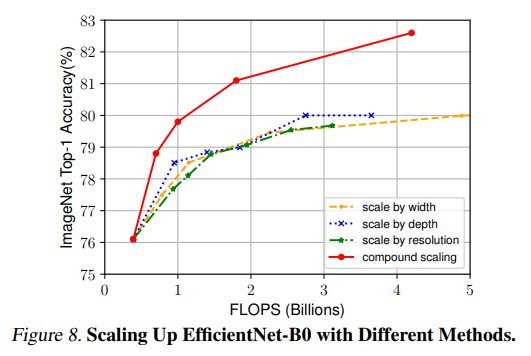
앞서 봤던 것처럼 1개 차원으로만 늘리면 80% 근처에서 성능이 좋아지지 않지만 $d,\ w,\ r$ 을 모두 늘렸을 때는 자원의 한계가 없다는 조건에서 성능향상이 계속 이어진다.

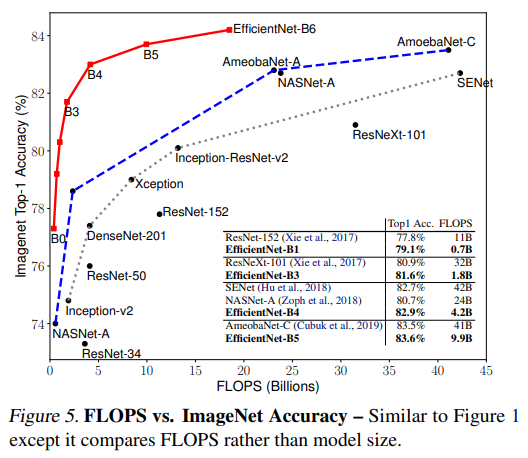
그 결과 기존의 모델에 비해 훨씬 낮은 연산량에 뛰어난 성능을 보여주고 있다.

Scaling ResNet & MobileNet

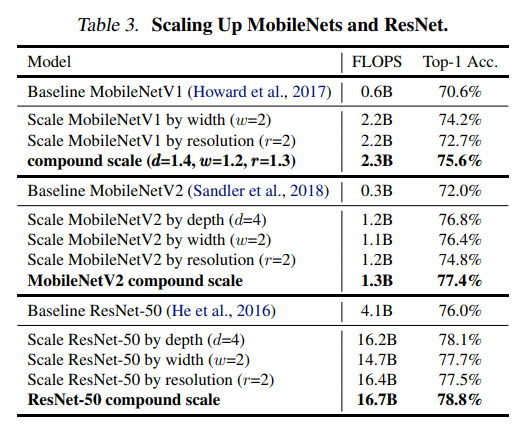
compound scaling은 EfficientNet뿐만 아니라 같은 방법으로 ResNet과 MobileNet을 크게 했을 때도 성능향상에 효과적이라고 밝히면서 compound scaling을 범용으로 쓸 수 있다고 뒷받침했다.

Epilogue

논문을 어떻게 읽어야 할지 다시 생각하게 된 연구다. 공부하다보면 곁다리로 함께 읽어야 하는 논문들이 나오기 마련인데 그 논문들도 완벽하게 이해해야 하는지, 아니면 주로 읽어야 하는 논문에 필요한 것만 빼먹고 덮어도 좋은지 잘 모르겠다. 사실 읽다보면 정신없이 읽으면서 파고들게 되는데 거기에서 중심잡기가 쉽지 않다.

Reference

iissaacc

이전 포스트

Feature Pyramid Network

다음 포스트