• updated Oct.19.21: SE block 구현

Prologue

CNN은 Convolution 연산을 통해 성능을 높여 사람의 인지능력보다 높은 성능의 모델을 개발해왔다. 그럼에도 이 연산은 spatial dimension$(\text{H, W})$과 depth dimension$(\text{C})$이 가진 신호를 마구 뒤섞는다는 점을 주목하고 channel 방향으로 늘어선 정보들도 활용할 수 있을 거라고 생각했다. 이 연구에서 제안한 방법으로 ILSVRC 2017에서 우승했다.

What did authors try to accomplish?

CNN은 입력 tensor와 $k\times k$ 크기의 kernel을 연산하면서 spatail dimension의 신호를 잘 정리해서 보여줄 수밖에 없었다. 수식으로 보면 좀더 직관적으로 와닿는다.

먼저 convolution 연산 $*$는 $\mathbf{F}:\mathbf{X}\in\mathbb{R}^{H'\times W'\times C'}\rarr\mathbf{U}\in\mathbb{R}^{H\times W\times C}$라고 정의하고 $\mathbf{u}_c$는 tensor $\mathbf{U}$에 속하는 임의의 원소이다. 집합 $\mathbf{V}$는 kernel $[\mathbf{v}_1,\ \mathbf{v}_2,\dots\mathbf{v}_c]$로 구성되어 있고 집합 $\mathbf{X}$는 $[\mathbf{x}_1,\ \mathbf{x}_2,\dots\mathbf{x}_{C'}]$로 구성되어 있다. 이 때, $\mathbf{X}\in\mathbb{R}^{H'\times W'\times C'}$이므로 임의의 kernel $\mathbf{v}_c$는 $C'$만큼의 channel을 가진다. 그래서 $\mathbf{u}_c\in\mathbb{R}^{H\times W}$이다.

이처럼 연구자들은 depth dimension 신호가 spatail dimension 신호에 뭍혀서 흐려지는 것을 발견했다. tensor의 channel 신호를 어떻게 하면 살릴 수 있을지, spatial 신호와 더불어 channel 신호도 잘 정리할 수 있으면 CNN이 가진 표현력을 더 높일 수 있을지 궁금했다.

What were key elements of the approach?

SE block

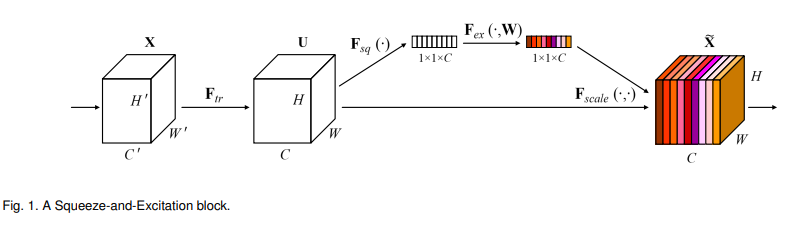
Squeeze and Excitation Block을 줄여서 SE block 또는 SENet이라고 부른다. 핵심은 spatial 정보를 가진 입력 tensor에 channel 방향의 신호를 한 번 더 강조해주는 거다. 이 block은 크게 3가지 과정으로 이루어져 있다.

1. Squeeze
   $\mathbb{R}^{H\times W\times C}$ 크기의 입력 tensor를 $\mathbb{R}^{1\times 1\times C}$ 크기로 찌부하고
2. Excitation
   각 channel이 가진 신호들을 적절히 살려서
3. Rescale
   입력 tensor와 depthwise로 곱한다.

Squeeze

앞서 살펴봤듯이 기존의 conv layer는 $(\text{H, W})$에 분포한 신호의 특성을 살리는데 집중한다. 이 연구에서는 channel 방향의 신호들은 제대로 볼 수 없다고 짚고 있다. 그래서 GlobalAveragePooling을 사용하고 있다. 이 layer는 $\mathbb{R}^{H\times W\times C}$ 크기의 tensor에서 $\mathbb{R}^{H\times W\times1}$에 분포한 신호들의 평균값을 내서 $\mathbb{R}^{1\times 1\times C}$로 바꾼다. 이 과정을 함수 $\mathbf{F}_{sq}$로 다시 정의할 수 있다.

Excitation

ReLU와 sigmoid를 activation function으로 하는 FC layer 2개로 이루어져있다. 좀 쉽게 생각하면 spatial dimension으로 한 번 정리한 신호를 depthwise로 한번 요약해서 2개의 hidden layer를 가진 작은 신경망에 입력한다고 할 수 있다.

전체 모델의 연산량을 제한하기 위해 $W_1\in\mathbb{R}^{\frac{C}{r}\times C}$, $W_2\in\mathbb{R}^{C\times\frac{C}{r}}$ 로 한다. $r$은 16이 가장 좋은 성능을 가진다고 했지만 실제로 활용할 때는 2의 거듭제곱으로 실험해서 정해야한다고 적고 있다.

연구에서는 가장 강한 신호에 연산자원을 우선적으로 할당한다는 차원에서 attention & gating mechanism이라고 소개하고 있다. 이게 무슨 말인지는 Attention is all you need를 읽어봐야 한다.

Rescale

$\mathbb{R}^{1\times 1\times C}$크기의 vector $\mathbf{s}$와 $\mathbb{R}^{H\times W\times C}$크기의 입력 tensor $\mathbf{U}$를 depthwise로 곱해서 같은 크기의 출력 tensor $\mathbf{\tilde{X}}$를 내보낸다.

Experiments

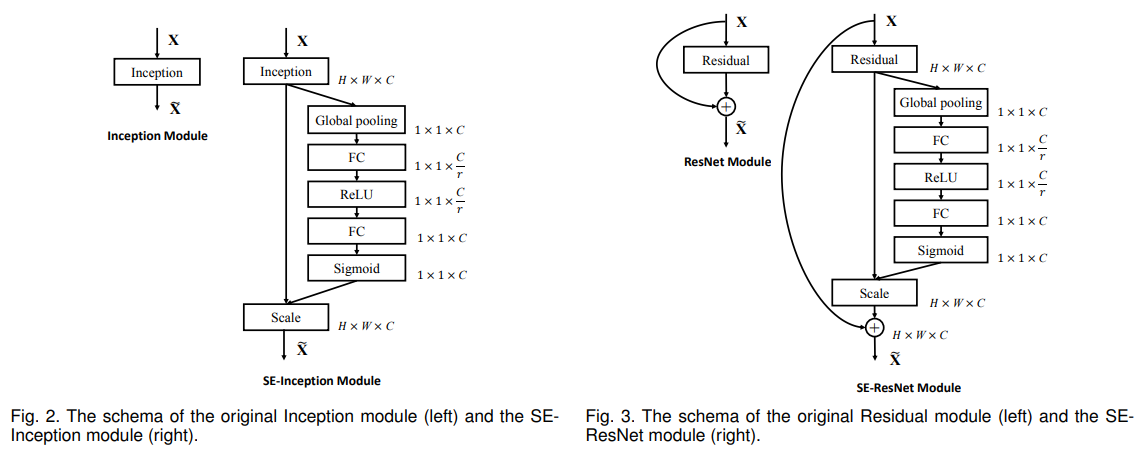
실험을 되게 많이 했던 연구다. SE block을 쌓아서 SENet을 만드는 것말고도 ResNet, Inception, MobileNet, ShuffleNet에 SE block을 붙여서 성능개선을 할 수 있는지도 살펴봤다. 결과는 SE block은 다른 구조를 가진 모델에 활용해도 성능개선을 보여줬다.

이 실험 말고도 SE block을 기존의 residual block 앞에 붙일지, 뒤에 붙일지, GlobalAveragePooling은 실제로 도움이 되는지 안 되는지도 살펴봤다. 이 부분을 읽으면 실험은 어떻게 하는 게 좋을지 감을 잡을 수 있을 것 같다.

Epilogue

연구에서 FC layer라고 계속 언급하고 있어서 처음에는 dense layer로 구현했다. 그런데 이 이미지에서 layer의 크기를 $\mathbb{R}^{1\times 1\times C}$로 서술하고 있어서 어쩌면 conv layer일 수도 있겠다는 생각이 들었다.

SE_dense_block
_____________________________________________________________
Layer (type)                    Output Shape         Param # 
=============================================================
input_1 (InputLayer)            [(None, 28, 28, 256) 0       
_____________________________________________________________
global_average_pooling2d (Globa (None, 256)          0       
_____________________________________________________________
dense (Dense)                   (None, 16)           4112    
_____________________________________________________________
dense_1 (Dense)                 (None, 256)          4352    
_____________________________________________________________
reshape (Reshape)               (None, 1, 1, 256)    0       
_____________________________________________________________
multiply (Multiply)             (None, 28, 28, 256)  0       
                                                             
=============================================================
Total params: 8,464
Trainable params: 8,464
Non-trainable params: 0
______________________________________________________________

중간에 reshape layer는 굳이 없어도 파이썬에서 알아서 브로드캐스팅을 잘 해줘서 없어도 된다. 이것 말고는 1x1 conv layer로 구현한 block과 큰 차이는 없는 것 같다.

SE_conv_block2
______________________________________________________________
Layer (type)                    Output Shape         Param #  
==============================================================
input_1 (InputLayer)            [(None, 28, 28, 256) 0        
______________________________________________________________
global_average_pooling2d_1 (Glo (None, 256)          0        
______________________________________________________________
reshape_1 (Reshape)             (None, 1, 1, 256)    0        
______________________________________________________________
conv2d (Conv2D)                 (None, 1, 1, 16)     4112     
______________________________________________________________
conv2d_1 (Conv2D)               (None, 1, 1, 256)    4352     
______________________________________________________________
multiply_1 (Multiply)           (None, 28, 28, 256)  0        
                                                              
==============================================================
Total params: 8,464
Trainable params: 8,464
Non-trainable params: 0
______________________________________________________________

물론 이렇게 하면 연구에 나온대로 엄밀하게 구현한 샘이 된다. 이 두 가지 사이에 성능차이가 있는지 봐야겠다.

Reference

1. Squeeze-and-Excitation Networks