• updated Mar.22.22: 오류수정, 내용보충, 모델구현

Prologue

신경망을 학습하는 것은 쉬운 일이 아니다. 특히 신경망이 깊어지면 학습하는데 닥치는 어려움은 크게 3가지가 있다.

1. Vanishing forward flow
2. Vanishing gradient
3. Training speed

1과 2는 weight initialization, ReLU, batch norm, identity mapping으로 극복할 수 있었지만 학습시간까지 줄일 수 없었다.

What did authors try to accomplish?

학습시간을 줄이려면 가장 간단하게는 얕은 모델을 만들어 쓰면 된다. 그러면 학습시간은 확실히 단축할 수 있지만 원하는 수준의 성능으로 끌어올릴 수 없을 거다.

전체 모델을 개발하고 나서 학습할 때는 layer를 듬성듬성 학습하고 테스트할 때는 전체 모델을 쓰는 방법을 쓰기로 했다. 그러기 위해서는 dropout에서 아이디어를 가져왔다.

What were key elements of approach?

Dropout

일반적으로 신경망은 수식으로 이렇게 표현한다.

이걸 조금 비틀어서 layer에 있는 $n$개의 node를 $p$의 확률로 0으로 만들어서 활성화가 안 되도록 하는 게 핵심이다.

이렇게 해서 너무 많은 node가 학습해서 overfitting이 일어나는 것을 막았고 mini_batch마다 다른 node가 활성화하므로 간접적으로 emsemble 효과까지 얻을 수 있다.

Residual block

ResBlock은 이미지에서 보는 것처럼 크게 2부분으로 나눌 수 있다.

1. Sequance of conv layer
2. Identity mapping

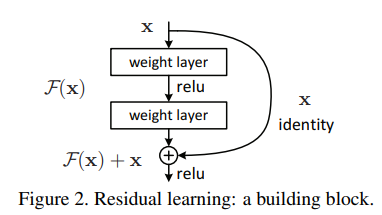
그러므로 ResBlock을 이렇게 표현한다.

위 식에서 $\small{W_s}$는 입력 tensor와 $\small{\mathcal{F}(\cdot)}$의 크기가 다를 때 쓴다.

Stochatic depth

Dropout은 model이 깊어지면 regularize 기능을 잃어버린다. 임의의 확률 $p$로 깨작깨작 node를 끄지말고 대범하게 sub-block을 건너뛰는 쪽을 선택했다.

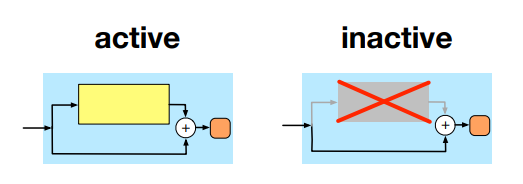
문제를 다시 정의해보면

$b_l$에 따라 두 가지 경우를 생각해보면

이렇게 하면 model의 연산량을 줄이면서 dropout의 효과도 그대로 가져올 수 있다. 그렇지만 우리에게 새로운 과제가 하나 더 주어진다. 최적의 확률 $p$를 찾는 것. model을 구성하는 block은 여러개가 있어서 연구에서는 $L$번째 block의 $p$를 $P_L$로 표현했다.

연구에서는 sub-block을 건너뛰는 방식을 2가지 제안했다.

1. Uniform
2. Linear decay

연구자들은 두 가지 경우를 비교하는 실험을 통해 1보다 2를 추천했다.

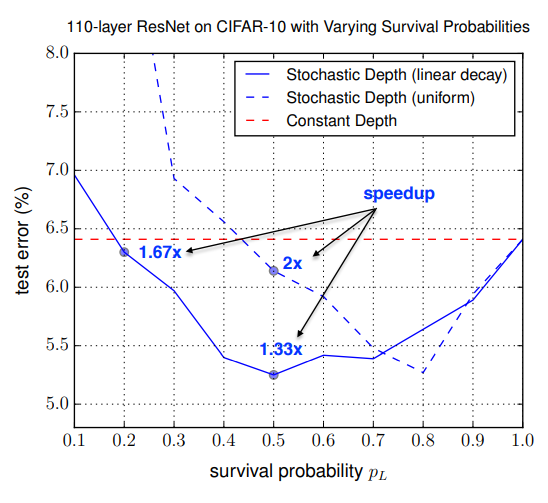
그래프에서 읽을 수 있듯이 같은 성능을 얻는데는 2가 효과적이다. 그러면서 minima로 수렴하는 속도가 빠르다고 하고 있는데 이건 왜 그렇게 주장하는지는 잘 모르겠다. linear decay의 경우에서 2배 가량 낮은 $P_L$로 counter party와 비슷한 성능을 얻을 수 있어서 그런 것 같다. 이 그래프가 연구자들이 $P_L=0.5$라고 추천하는 근거로 삼고 있다.

Linear decay

연구자들이 추천하는대로 2를 구현하면 아래 이미지처럼 된다.

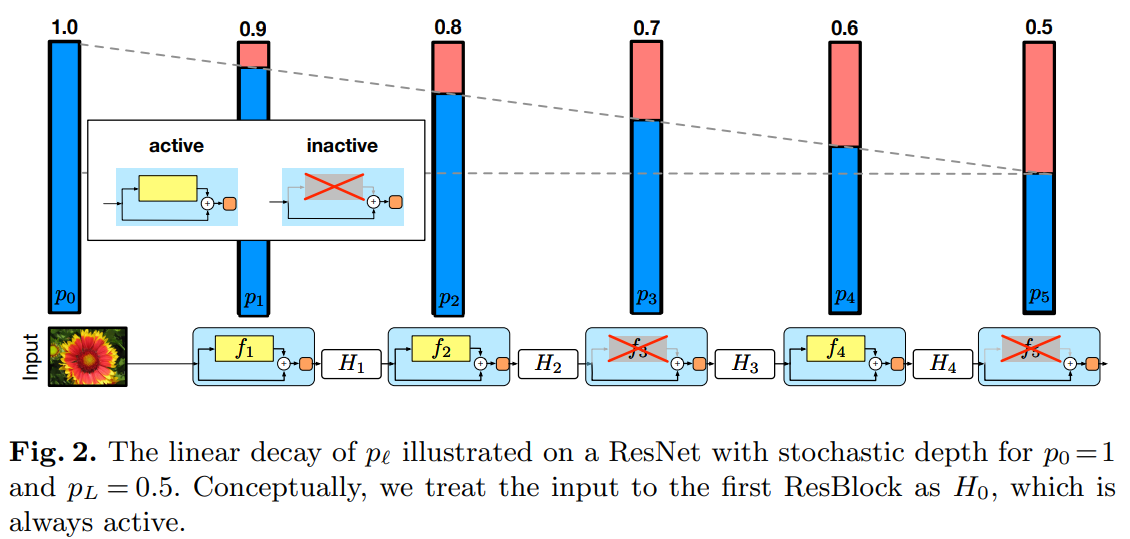
물론 이미지처럼 5개 block으로 구성하고 있는 model은 찾아보기 힘들다. 그래서 $P_L$을 decay하는 방법을 이렇게 제안했다.

이 방법을 활용하면 연구자들의 주장처럼 가장 마지막에 있는 block의 $p$는 $P_L$로 정할 수 있다. 9개의 ResBlock으로 구성하는 model의 $p_l$을 계산해보면 아래와 같은 결과를 얻을 수 있다.

0.9444444444444444
0.8888888888888888
0.8333333333333334
0.7777777777777778
0.7222222222222222
0.6666666666666667
0.6111111111111112
0.5555555555555556
0.5

Epliogue

연구자들은 0.5를 추천했지만 모든 모델에서 유효할지를 두고 실험을 해봤다.

Dataset: CIFAR10
Augmentation: 4 padded random crop, horizontal flop
optimizer: SGD(lr=1e-2, momentum=9e-1)

이렇게 해서 20 layer ResNet에 stochastic depth를 추가해서 학습해봤다. 연구자들이 제안했던 0.5를 $P_L$로 하는 model, 그리고 0.36을 $P_L$로 하는 model을 비교했다. 연구에서 기대하는 것처럼 stochastic depth가 regularizer역할을 해서 학습하는 동안 두 모델에서 overfitting이 나타나지 않았다. 그렇지만 모델의 크기에 비해 $P_L$이 과도하게 높으면 오히려 학습을 방해한다고 관찰할 수 있었다.

Reference

1. Deep Networks with Stochastic Depth