Triplet Loss

iissaacc·2022년 1월 19일

paper reading

목록 보기

14/20

Prologue

그동안 분류과제에서 loss function은 주로 softmax를 기반으로 한 cross entorpy를 썼다. 현실에서는 원하는 만큼의 data를 확보하는 게 어려울 수도 있고 같은 category안에 있는 data를 분류해야 할 때도 있다. 이런 문제를 해결하려고 FaceNet에서 제안한 방법이 triplet loss다. 과장을 좀더 보태서 거의 data 수만큼의 class를 구분할 수 있다. 이런 과제를 N-way K-shot problem이라고 부른다.

Triplet loss

FaceNet에서는 얼굴에서 추출한 $\mathbb{R}^d$ 차원의 embeding을 $\text{L2 norm}$ 으로 유사성을 비교하는 방법이다. triplet이 생소한데 찾아보자.

Triplet: noun
a set or succession of three similar things.

요소 3개. 같은 범주. 오케

supervised model은 L2 loss혹은 cross entropy loss로 pred와 label의 거리를 최대한 가깝게 하는 모양을 가진다. tirplet loss는 이름처럼 3가지 data를 요구한다.

anchor: 기준 data
positive: anchor와 같은 class에 속하는 data
negative: anchor와 다른 class에 속하는 data

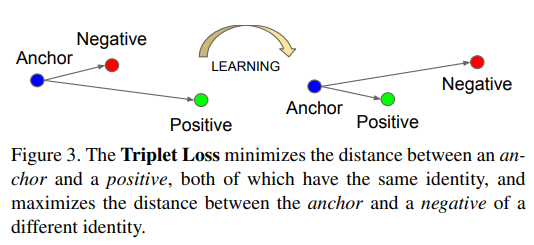
이렇게 해서 anchor와 positive의 거리는 가깝게 하고, anchor와 negative의 거리는 멀리 하는게 triplet loss의 목표다. 복잡하니까 이미지로 보자.

Equation

먼저 이미지대로 anchor와 positive와의 거리가 anchor와 negative와의 거리보다 짧아야 한다.

||f(A)-f(P)||^2_2\le||f(A)-f(N)||^2_2

이걸 정리하면 식은 이런 모양이 된다.

||f(A)-f(P)||^2_2-||f(A)-f(N)||^2_2\le0

network가 이 문제를 푸는 아주 쉬운 방법은 $f(A),\ f(P),\ f(N)$ 이 전부 0으로 수렴하는 경우다. 이 일이 일어나는 일은 아주 드물지만 그래도 확실히 하기 위해 threshold, 혹은 margin을 걸어둔다.

||f(A)-f(P)||^2_2-||f(A)-f(N)||^2_2+\alpha\le0

그래서 triplet loss는 이렇게 생겼다.

\text{L}=max\left(||f(A)-f(P)||^2_2-||f(A)-f(N)||^2_2+\alpha,\ 0\right)

loss function $\text{L}$ 을 최소화하는 방향으로 network가 학습하게 된다. 그림에서 봤듯이 우리는 $||f(A)-f(P)||_2^2$ 이 $0$ 에 수렴하고 $||f(A)-f(N)||_2^2$ 은 $||f(A)-f(P)||_2^2+\alpha$ 보다 크게 하는 것을 목표로 학습하게 된다. 그러면 우리는 data를 어떻게 뽑아야 할까?

Triplet mining

dataset에서 anchor, positive, negative를 뽑는 일을 triplet mining이라고 한다. data를 뽑았을 때 $||f(A)-f(N)||_2^2$ 의 크기에 따라 난이도가 3가지로 나뉘어진다.

1. Easy negatives

$||f(A)-f(P)||^2_2+\alpha\lt||f(A)-f(N)||^2_2$

2. Semi hard negatives

$||f(A)-f(P)||^2_2\lt||f(A)-f(N)||^2_2\lt||f(A)-f(P)||^2_2+\alpha$

3. Hard negatives

$||f(A)-f(N)||^2_2\lt||f(A)-f(P)||^2_2$

쉽게 이미지로 보면 이렇다.

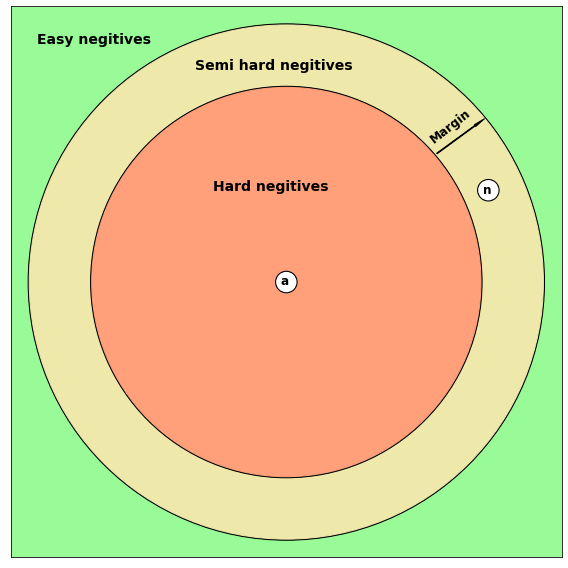
여기에서 빨간원의 반지름이 $||f(A)-f(P)||_2^2$ , 원점으로부터 $n$ 까지의 거리를 $||f(A)-f(N)||_2^2$ 이라고 할 때 3가지 난이도는 이미지처럼 결정된다. 이 때 easy negatives만 골라서 학습하면 loss가 낮아서 학습이 안 되거나 느리다. 그래서 연구에서는 학습속도 향상을 위해 의도적으로 $\text{argmax}\left(||f(A)-f(P)||^2_2\right)$ 와(hard positive) $\text{argmin}\left(||f(A)-f(N)||^2_2\right)$ 를(hard negative) 찾아서 triplet을 구성하게 했다. 이것을 찾는 과정을 hard mining이라고 부른다.

먼저 hard positive만 골라내면 자연스레 hard negative를 고르는 일이 수월해질 거다. 다만 전체 dataset에서 hard positive와 hard negative만 고르면 연산효율도 많이 떨어질 뿐만 아니라 global minima를 제대로 못 찾을 수도 있어서 semi hard negatives만 만족해도 학습에 사용하도록 했다. 이렇게 하는 편이 학습에 더 안정적이라고 적고 있다.

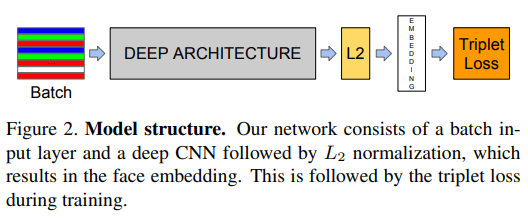
그러면 전체 netkwork의 구조는 위와 같을텐데 어떻게 하면 3가지를 효율적으로 고를 수 있을까?

Online vs Offline

다른 연구나 관련 글을 읽으면 가끔 나오는 용어인데 하나로 합의가 안 된 것 같다.

Offline learning
1. batch gradient descent를 다른 이름으로 offline learning이라고 부른다.
2. 혹은 학습에 고정된 크기의 dataset을 쓸 때 이렇게 부른다.

Online learning
1. offline learning과는 반대되는 개념으로 stochastic gradient descent를 online learning으로 부른다.
2. 혹은 어떤 이유로 인해 학습 data를 어딘가로부터 실시간으로 받와야 할 때 이렇게 부른다.

연구에서는 아마 두 가지 모두 1번에 해당하는 것 같다. 전체 dataset을 대상으로 hard mining을 할 때 앞서 언급한 부작용들을 피하기 위해 두 가지 방법을 제시했다.

Offline learning: weight를 $n$ 번 업데이트할 때마다(every n steps) 이전에 hard mining할 때 계산한 distance를 활용해서 hard mining을 한다.
Online learning: mini batch 안에서 hard mining을 한다.

두 가지 중에 online learning을 주로 소개했다. 연구자들은 online learning이라고 해서 SGD를 쓰지 않고 mini batch gradient descent를 활용했는데 그러면서 동시에 offline learning의 효과도 보고싶었는지 batch size를 triplet 1800개로 했다.

Epilogue

triplet loss를 구현하는 것은 어려운 일은 아니지만 아무리 생각해도 전체 dataset에서 mini batch를 구성하고 embeding을 만든 다음에 distance를 계산해서 triplet을 만드는 과정에서 bottleneck 없이 pipeline을 만드는 게 쉽지 않을 것 같다. github 한 번 뒤져봐야겠다.